| Citation: | Jingmin Pi, Tianxiu Lu, Waseem Anwar, Zhiwen Mo. FURTHER STUDIES OF TOPOLOGICAL TRANSITIVITY IN NON-AUTONOMOUS DISCRETE DYNAMICAL SYSTEMS[J]. Journal of Applied Analysis & Computation, 2024, 14(3): 1508-1521. doi: 10.11948/20230264 |
FURTHER STUDIES OF TOPOLOGICAL TRANSITIVITY IN NON-AUTONOMOUS DISCRETE DYNAMICAL SYSTEMS
-
Abstract
In this paper, notions related to transitivity in autonomous discrete dynamical systems are generalized to non-autonomous discrete dynamical systems. Some sufficient conditions or necessary conditions of transitive were given. Then, it is obtained that the mapping sequence $f_{1, \infty}=(f_{1}, f_{2}, \cdots)$ is $\mathcal{P}$-chaotic if and only if the mapping sequence $f_{n, \infty}=(f_{n}, f_{n+1}, \cdots), \forall n \in \mathbb{N}$ $(\mathbb{N}=\{1, 2, \cdots\})$ would also be $\mathcal{P}$-chaotic. Where $\mathcal{P}$-chaos represents one of the following six properties: transitive, mixing, weakly mixing, syndetically transitive, strongly transitive, and $\mathbb{Z}$-transitive. Finally, an example is given to show that the condition ‘the space has no isolated point’ cannot be removed, and a $\mathcal{P}$-chaotic non-autonomous mapping sequence is provided.
-
Keywords:
- Non-autonomous discrete dynamical systems /
- transitivity /
- mixing
-

-
References
[1] S. Ahmadi, X. Wu and G. Chen, Topological chain and shadowing properties of dynamical systems on uniform spaces, Topol. Appl., 2020, 275, 107153. doi: 10.1016/j.topol.2020.107153 [2] W. Anwar, T. Lu and X. Yang, Sensitivity of iterated function systems under the product operation, Results Math., 2022, 77, 185. doi: 10.1007/s00025-022-01669-6 [3] J. Banks, Regular periodic decompositions for topologically transitive maps, Ergod. Theor. Dyn. Syst., 1997, 17, 505–529. doi: 10.1017/S0143385797069885 [4] G. Birkhoff, Dynamical Systems, American Mathematical Society, Washington, 2008. [5] L. Block and D. Ledis, Topological conjugacy, transitivity and patterns, Topol. Appl., 2014, 167, 53–61. doi: 10.1016/j.topol.2014.03.003 [6] Z. Chen, J. Li and L. Jie, On multi-transitivity with respect to a vector, Sci. China Math., 2014, 57, 1639–1648. doi: 10.1007/s11425-014-4797-z [7] M. Javaheri, Hypercyclic and topologically transitive semigroups of composition operators, Topol. Appl., 2014, 164, 105–112. doi: 10.1016/j.topol.2013.12.004 [8] D. Kwietniak and P. Oprocha, On weak mixing, minimality and weak disjointness of all iterates, Ergod. Theor. Dyn. Syst., 2012, 32, 1661–1672. doi: 10.1017/S0143385711000599 [9] J. Li, C. Liu, S. Tu and T. Yu, Sequence entropy tuples and mean sensitive tuples, Ergod. Theor. Dyn. Syst., 2024, 44, 184–203. doi: 10.1017/etds.2023.5 [10] J. Li, X. Ye and T. Yu, Equicontinuity and sensitivity in mean forms, J. Dyn. Differ. Equ., 2022, 34, 133–154. doi: 10.1007/s10884-021-09945-9 [11] J. Li, X. Ye and T. Yu, Mean equicontinuity, complexity and applications, Discrete contin. dyn. syst., 2021, 41, 359–393. doi: 10.3934/dcds.2020167 [12] R. Li, Y. Zhao and H. Wang, Stronger forms of transitivity and sensitivity for nonautonomous discrete dynamical systems and Furstenberg families, J. Dyn. Control Syst., 2020, 26, 109–126. doi: 10.1007/s10883-019-09437-6 [13] G. Liao, L. Wang and Y. Zhang, Transitivity, mixing and chaos for a class of set-valued mappings, Sci. China Math., 2006, 49, 1–8. doi: 10.1007/s11425-004-5234-5 [14] J. Pi, T. Lu and Y. Chen, Collective sensitivity and collective accessibility of non-autonomous discrete dynamical systems, Fractal. Fract., 2022, 6, 535. doi: 10.3390/fractalfract6100535 [15] J. Pi, T. Lu and Y. Xue, Transitivity and shadowing properties of non-autonomous discrete dynamical systems, Int. J. Bifurcat. Chaos, 2022, 32, 2250246. doi: 10.1142/S0218127422502467 [16] H. Shao, Y. Shi and H. Zhu, Estimations of topological entropy for nonautonomous discrete systems, J. Differ. Equ. Appl., 2016, 22, 474–484. doi: 10.1080/10236198.2015.1107055 [17] R. Thakur and R. Das, Transitivity and sensitivity of iterated function systems via Furstenberg families, Aequationes math., 2020, 94, 1123–1140. doi: 10.1007/s00010-020-00757-8 [18] R. Vasisht and R. Das, Generalizations of expansiveness in non-autonomous discrete systems, B. Iran. Math. Soc., 2022, 48, 417–433. doi: 10.1007/s41980-020-00525-z [19] X. Wu, X. Ding, T. Lu and J. Wang, Topological dynamics of Zadeh's extension on the space of upper semi-continuous fuzzy sets, Int. J. Bifurcat. Chaos, 2017, 27, 1750165. doi: 10.1142/S0218127417501656 [20] X. Xie and J. Yin, On the eventual shadowing property and eventually shadowable point of set-valued dynamical systems, Acta. Math. Sin., 2022, 38, 1105–1115. doi: 10.1007/s10114-022-1041-6 [21] X. Yang, T. Lu and W. Anwar, Chaotic properties of a class of coupled mapping lattice induced by fuzzy mapping in non-autonomous discrete systems, Chaos Soliton Fract., 2021, 148, 110979. doi: 10.1016/j.chaos.2021.110979 [22] X. Yang, T. Lu, J. Pi and Y. Jiang, On shadowing system generated by a uniformly convergent mappings sequence, J. Dyn. Control Syst., 2022, 28, 238. -
-
-
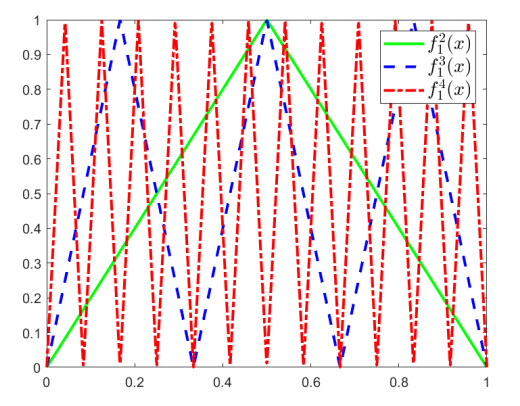
Figure 1.
The function images of
$ f_1^2, f_1^3 $ $ f_1^4 $




 DownLoad:
DownLoad: