| Citation: |
Tiansi Zhang, Lihong Qiu, Dianli Zhao, Sanling Yuan. OSCILLATION AND SURVIVAL ANALYSIS OF GENERALIZED STOCHASTIC LOGISTIC MODELS WITH PIECEWISE CONSTANT ARGUMENT[J]. Journal of Applied Analysis & Computation, 2024, 14(3): 1522-1542. doi: 10.11948/20230271
|
OSCILLATION AND SURVIVAL ANALYSIS OF GENERALIZED STOCHASTIC LOGISTIC MODELS WITH PIECEWISE CONSTANT ARGUMENT
-
Abstract
The paper focuses on oscillation and survival analysis for a class of generalized stochastic logistic equations with piecewise constant argument. The existence of global positive solution is proved firstly. Then the necessary and sufficient conditions under which the population will be almost surely extinct and persistent are investigated. Furthermore, we study the condition for oscillation of the equation with constant coefficients, and the result shows that the solution oscillates around a new positive point induced by the noise. Finally, numerical experiments are given for several examples to support the results.
-
-
References
[1] M. Akhmet, D. Arugaslan Cincin and N. Cengiz, Exponential stability of periodic solutions of recurrent neural networks with functional dependence on piecewise constant argument, Turkish Journal of Mathematics, 2018, 42, 272–292. doi: 10.3906/mat-1606-138 [2] M. Akhmet, M. Tleubergenova and Z. Nugayeva, Unpredictable and Poisson Stable Oscillations of Inertial Neural Networks with Generalized Piecewise Constant Argument, ENTROPY, 2023. DOI: 10.3390/e25040620. [3] M. S. Alwan, X. Liu and W. Xie, Comparison principle and stability of differential equations with piecewise constant arguments, Journal of the Franklin Institute, 2013, 350, 211–230. doi: 10.1016/j.jfranklin.2012.08.016 [4] H. Assel, M. A. Hammami and M. Miraoui, Dynamics and oscillations for some difference and differential equations with piecewise constant arguments, Asian Journal of Control, 2022, 24, 1143–1151. doi: 10.1002/asjc.2619 [5] M. L. Buyukkahraman, Existence of periodic solutions to a certain impulsive differential equation with piecewise constant arguments, Eurasian Mathematical Journal, 2022, 13, 54–60. [6] Q. J. Chen, Z. J. Liu, Y. S. Tan and J. Yang, Analysis of a stochastic hybrid population model with impulsive perturbations and Allee effect, J. App. Math. Comp., 2022, 69, 565–587. [7] K. L. Cooke and J. Wiener, Retarded differential equations with piecewise constant delays, J. Math. Anal. Appl., 1984, 99, 265–297. doi: 10.1016/0022-247X(84)90248-8 [8] Y. X. Gao and S. Q. Tian, Dynamics of a stochastic predator-prey model with two competitive preys and one predator in a polluted environment, Japan Journal of Industrial and Applied Mathematics, 2018, 35, 861–889. [9] K. Gopalsamy and P. Liu, Persistence and global stability in a population model, J. Math. Anal. Appl., 1998, 224, 59–80. doi: 10.1006/jmaa.1998.5984 [10] D. J. Higham, An algorithmic introduction to numerical simulation of stochastic differential equations, SIAM Rev., 2001, 43, 525–546. doi: 10.1137/S0036144500378302 [11] J. Jacod and P. Protter, Probability Essentials, Universitext, Spring-Verlag, New York, NY, 2000. [12] W. M. Ji, On a population model with Allee effects and environmental perturbations, J. App. Math. Comp., 2020, 64, 749–764. doi: 10.1007/s12190-020-01377-w [13] M. Jovanovic and M. Vasilova, Dynamics of non-autonomous stochastic Gilpin-Ayala competition model with time-varying delays, Appl. Math. Comput., 2013, 219, 6946–6964. [14] F. Karakoc, Oscillation of a first order linear impulsive delay differential equation with continuous and piecewise constant arguments, Hacettepe Journal of Mathematics and Sttistics, 2018, 47, 601–613. [15] F. Karakoc, A. O. Unal and H. Bereketoglu, Oscillation of nonlinear impulsive differential equations with piecewise constant arguments, Electronic Journal of Qualitative Theory of Differential Equations, 2013, 49, 1–12. [16] F. Karakoc, A. Unal and H. Bereketoglu, Oscillation of a nonlinear impulsive differential equation system with piecewise constant argument, Advances in Difference Equations, 2018. DOI: 10.1186/s13662-018-1556-4. [17] X. Li, A. Gray, D. Jiang and X. Mao, Sufficient and necessary conditions of stochastic permanence and extinction for stochastic logistic populations under regime switching, J. Math. Anal. Appl., 2011, 376, 11–28. doi: 10.1016/j.jmaa.2010.10.053 [18] M. Liu and M. L. Deng, Analysis of a stochastic hybrid population model with Allee effect, App. Math. Com., 2020, 364, 124582. doi: 10.1016/j.amc.2019.124582 [19] M. Liu and K. Wang, A remark on stochastic Logistic model with diffusion, Appl. Math. Comput., 2014, 228, 141–146. [20] C. Lu, Q. Ma and X. H. Ding, Persistence and extinction for stochastic logistic model with levy noise and impulsive perturbation, Elec. J. Diff. Equa., 2015. ID: 247. [21] Q. Luo and X. Mao, Stochastic population dynamics under regime switching II, J. Math. Anal. Appl., 2009, 355, 577–593. doi: 10.1016/j.jmaa.2009.02.010 [22] X. Mao, Stochastic Differential Equations and Applications, Horwood Publishing, Chichester, 1997. [23] X. Mao, G. Marion and E. Renshaw, Environmental Brownian noise suppresses explosions in population dynamics, Stochastic Process. Appl., 2002, 97, 95–110. doi: 10.1016/S0304-4149(01)00126-0 [24] Y. Mu and W. C. Lo, Stochastic dynamics of populations with refuge in polluted turbidostat, Chaos Solitons and Fractals, 2021, 147, 110963. doi: 10.1016/j.chaos.2021.110963 [25] J. D. Murray, Mathematical Biology: I. An Introduction, Springer-Verlag, NJ, 1989. [26] W. X. Ning, Z. J. Liu and R. H. Tan, Analysis of a stochastic competitive model with saturation effect and distributed delay, Methodology and Computing in Applied Probability, 2021, 23, 1435–1459. doi: 10.1007/s11009-020-09824-8 [27] I. Ozturk and F. Bozkurt, Stability analysis of a population model with piecewise constant arguments, Nonlinear Analysis: RWA, 2011, 12, 1532–1545. doi: 10.1016/j.nonrwa.2010.10.011 [28] I. Ozturk, F. Bozkurt and F. Gurcan, Stability analysis of a mathematical model in a microcosm with piecewise constant arguments, Mathematical Biosciences, 2012, 240, 85–91. [29] S. P. Rajasekar, M. Pitchaimani and Q. X. Zhu, Dynamic threshold probe of stochastic SIR model with saturated incidence rate and saturated treatment function, Physica A-Statistical Mechanics and its Applications, 2019. DOI: 10.1016/j.physa.2019.122300. [30] S. M. Shah and J. Wiener, Advanced differential equations with piecewise constant argument deviations, Int J. Math. Math. Soc., 1983, 6, 671–703. [31] F. Wei and K. Wang, The existence and uniqueness of the solution for stochastic functional differential equations with infinite delay, J. Math. Anal. Appl., 2008, 331, 516–531. [32] X. B. Zhang and R. J. Liu, The stationary distribution of a stochastic SIQS epidemic model with varying total population size, App. Math. Lett., 2021, 116, 106974. [33] L. Zu, D. Q. Jiang and D. O'Regan, Periodic solution for a stochastic non-autonomous Predator-Prey model with holling II functional response, Acta Applicandae Mathematicae, 2019, 161, 89–105. -
-
Figures(3)
Export File
Citation
Tiansi Zhang, Lihong Qiu, Dianli Zhao, Sanling Yuan. OSCILLATION AND SURVIVAL ANALYSIS OF GENERALIZED STOCHASTIC LOGISTIC MODELS WITH PIECEWISE CONSTANT ARGUMENT[J]. Journal of Applied Analysis & Computation, 2024, 14(3): 1522-1542. doi: 10.11948/20230271
Format
Content
DownLoad:
-
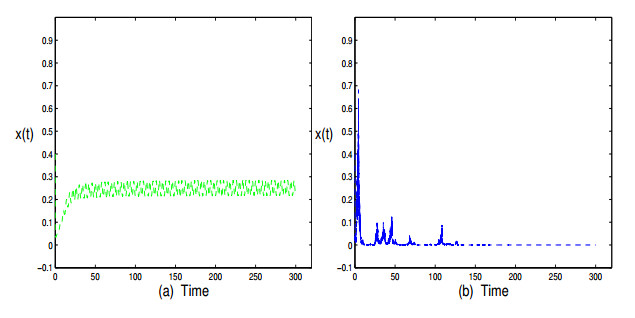
Figure 1.
(a) : the trajectory of the determined equation (5.3). (b) : the trajectory of the stochastic equation (5.2) with
$ \Delta t=0.001 $ -
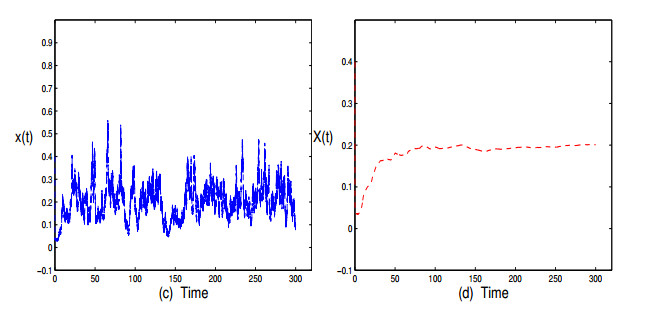
Figure 2.
(c): the trajectory of equation (5.4) with
$ \Delta t=0.001 $ $ X(t) $ -
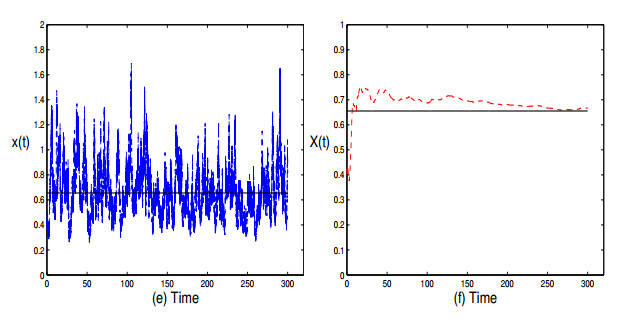
Figure 3.
The blue line in (e) is the trajectory of equation (5.5) with
$ \Delta t=0.001 $ $ X(t) $ $ \widetilde{x}= 0.655 $