| Citation: | Naima Hamel, Noureddine Benrabia, Mourad Ghiat, Hamza Guebbai. DEVELOPING A NEW CONJUGATE GRADIENT ALGORITHM WITH THE BENEFIT OF SOME DESIRABLE PROPERTIES OF THE NEWTON ALGORITHM FOR UNCONSTRAINED OPTIMIZATION[J]. Journal of Applied Analysis & Computation, 2024, 14(1): 458-472. doi: 10.11948/20230268 |
DEVELOPING A NEW CONJUGATE GRADIENT ALGORITHM WITH THE BENEFIT OF SOME DESIRABLE PROPERTIES OF THE NEWTON ALGORITHM FOR UNCONSTRAINED OPTIMIZATION
-
Abstract
The conjugate gradient method and the Newton method are both numerical optimization techniques. In this paper, we aim to combine some desirable characteristics of these two methods while avoiding their drawbacks, more specifically, we aim to develop a new optimization algorithm that preserves some essential features of the conjugate gradient algorithm, including the simplicity, the low memory requirements, the ability to solve large scale problems and the convergence to the solution regardless of the starting vector (global convergence). At the same time, this new algorithm approches the quadratic convergence behavior of the Newton method in the numerical sense while avoiding the computational cost of evaluating the Hessian matrix directly and the sensitivity of the selected starting vector. To do this, we propose a new hybrid conjugate gradient method by linking (CD) and (WYL) methods in a convex blend, the hybridization paramater is computed so that the new search direction accords with the Newton direction, but avoids the computational cost of evaluating the Hessian matrix directly by using the secant equation. This makes the proposed algorithm useful for solving large scale optimization problems. The sufficient descent condition is verified, also the global convergence is proved under a strong Wolfe Powel line search. The numerical tests show that, the proposed algorithm provides the quadratic convergence behavior and confirm its efficiency as it outperformed both the (WYL) and (CD) algorithms.
-

-
References
[1] Z. M. Abdullah and I. K. Jamalaldeen, A new hybrid of DY and CGSD conjugate gradient methods for solving unconstrained optimization problems, Tik. J. of Pure Sci., 2021, 26(5), 86–91. doi: 10.25130/tjps.v26i5.183 [2] A. B. Abubakar, et al, A Liu-Storey-type conjugate gradient method for unconstrained minimization problem with application in motion control, Journal of King Saud University - Science, 2022, 34(4), 101923. doi: 10.1016/j.jksus.2022.101923 [3] A. B. Abubakar, P. Kumam, M. Malik, P. Chaipunya and A. H. Ibrahim, A hybrid FR-DY conjugate gradient algorithm for unconstrained optimization with application in portfolio selection, AIMS Mathematics, 2021, 6(6), 6506–6527. doi: 10.3934/math.2021383 [4] A. B. Abubakar, P. Kumam, M. Malik and A. H. Ibrahim, A hybrid conjugate gradient based approach for solving unconstrained optimization and motion control problems, Mathematics and Computers in Simulation, 2022, 201, 640–657. doi: 10.1016/j.matcom.2021.05.038 [5] N. Andrei, A hybrid conjugate gradient algorithm with modified secant condition for unconstrained optimization as a convex combination of Hestenes-Stiefel and Dai-Yuan algorithms, Studies in Informatics and Control, 2008, 17(4), 373–392. [6] N. Andrei, Another hybrid conjugate gradient algorithm for unconstrained optimization, Numer. Algor., 2008, 47(2), 143–156. doi: 10.1007/s11075-007-9152-9 [7] N. Andrei, An unconstrained optimization test functions, Collection. Adv. Model. Optim., 2008, 10(1), 147–161. [8] Y. H. Dai and Y. Yuan, A nonlinear conjugate gradient method with a strong global convergence property, SIAM Journal on optimization, 1999, 10(1), 177–182. doi: 10.1137/S1052623497318992 [9] S. S. Djordjević, New conjugate gradient method as a convex combination of LS and FR methods, Acta Mathematica Scientia, 2019, 39B(1), 214–228. doi: 10.3969/j.issn.0252-9602.2019.01.017 [10] E. D. Dolan and J. J. Moré, Benchmarking optimization software with performance profiles, Math. Program., 2002, 91(2), 201–213. doi: 10.1007/s101070100263 [11] N. J. Fanar and M. A. Ghada, A new hybrid conjugate gradient algorithm as a convex combination of MMWU and RMIL nonlinear problems, Journal of Interdisciplinary Mathematics, 2021, 24(3), 637–655. doi: 10.1080/09720502.2020.1815346 [12] R. Fletcher, Practical Methods of Optimization. Unconstrained Optimization, John Wiley and Sons, New York, 1987. [13] R. Fletcher and C. M. Reeves, Function minimization by conjugate gradients, Comput. J., 1964, 7(2), 149–154. doi: 10.1093/comjnl/7.2.149 [14] J. C. Gilbert and J. Nocedal, Global convergence properties of conjugate gradient methods for optimization, SIAM J. Optimizat., 1992, 2(1), 21–42. doi: 10.1137/0802003 [15] M. R. Hestenes and E. L. Stiefel, Methods of conjugate gradients for solving linear systems, J. Res. Natl. Bur. Stand., 1952, 49(6), 409–436. doi: 10.6028/jres.049.044 [16] H. Huang, Z. Wei and S. Yao, The proof of the sufficient descent condition of the Wei-Yao-Liu conjugate gradient method under the strong Wolfe-Powell line search, Applied Mathematics and Computation, 2007, 189, 1241–1245. doi: 10.1016/j.amc.2006.12.006 [17] J. K. Liu and S. J. Li, New hybrid conjugate gradient method for unconstrained optimization, Applied Mathematics and Computation, 2014, 245, 36–43. doi: 10.1016/j.amc.2014.07.096 [18] Y. Liu and C. Storey, Efficient generalized conjugate gradient algorithms, part 1: Theory, J. Optim. Theory. Appl., 1991, 69(1), 129–137. doi: 10.1007/BF00940464 [19] Y. Liu, Z. Zhu and B. Zhang, Two sufficient descent three-term conjugate gradient methods for unconstrained optimization problems with applications in compressive sensing, J. Appl. Math. Comput., 2022, 68, 1787–1816. doi: 10.1007/s12190-021-01589-8 [20] S. Narayanan and P. Kaelo, A linear hybridization of Dai-Yuan and Hestenes-Stiefel conjugate gradient method for unconstrained optimization, Numer. Math. Theor. Meth. Appl., 2021, 14, 527–539. doi: 10.4208/nmtma.OA-2020-0056 [21] H. Oviedo, Implicit steepest descent algorithm for optimization with orthogonality constraints, Optimization Letters, 2022, 16(6), 1773–1797. doi: 10.1007/s11590-021-01801-5 [22] E. Polak and G. Ribiére, Note sur la convergence de méthodes de directions conjugués, Rev. Fr. Inf. Rech. Oper., 1969, 3(16), 35–43. [23] B. T. Polyak, The conjugate gradient method in extremal problems, USSR Comput. Math. Math. Phys., 1969, 9(4), 94–112. doi: 10.1016/0041-5553(69)90035-4 [24] B. T. Polyak, Newton's method and its use in optimization, European Journal of Operational Research, 2007, 181, 1086–1096. doi: 10.1016/j.ejor.2005.06.076 [25] A. Samson, Nonlinear Programming: Theories and Algorithms of Some Unconstrained Optimization Methods (Steepest Descent and Newton's Method), International Journal of Engineering and Management Research, 2020, 10(2), 1–12. [26] H. J. M. Shi, Y. Xie, R. Byrd and J. Nocedal, A noise-tolerant quasi-Newton algorithm for unconstrained optimization, SIAM Journal on Optimization, 2022, 32(1), 29–55. doi: 10.1137/20M1373190 [27] Y. Wang, F. Alpak, G. Gao, C. Chen, J. Vink, T. Wells and F. Saaf, An efficient bi-objective optimization workflow using the distributed quasi-Newton method and its application to well-location optimization, SPE Journal, 2022, 21(1), 364–380. [28] H. A. Wasi and M. A. K. Shiker, Nonlinear conjugate gradient method with modified armijo condition to solve unconstrained optimization, J. Phys. : Conf. Ser., 2021, 1818, 1–7. [29] Z. Wei, S. Yao and L. Liu, The convergence properties of some new conjugate gradient methods, Applied Mathematics and Computation, 2006, 183, 1341–1350. [30] X. P. Zhao, J. C. Yao and Y. Yao, A nonmonotone gradient method for constrained multiobjective optimization problems, J. Nonlinear Var. Anal., 2022, 6(6), 693–706. -
-
-
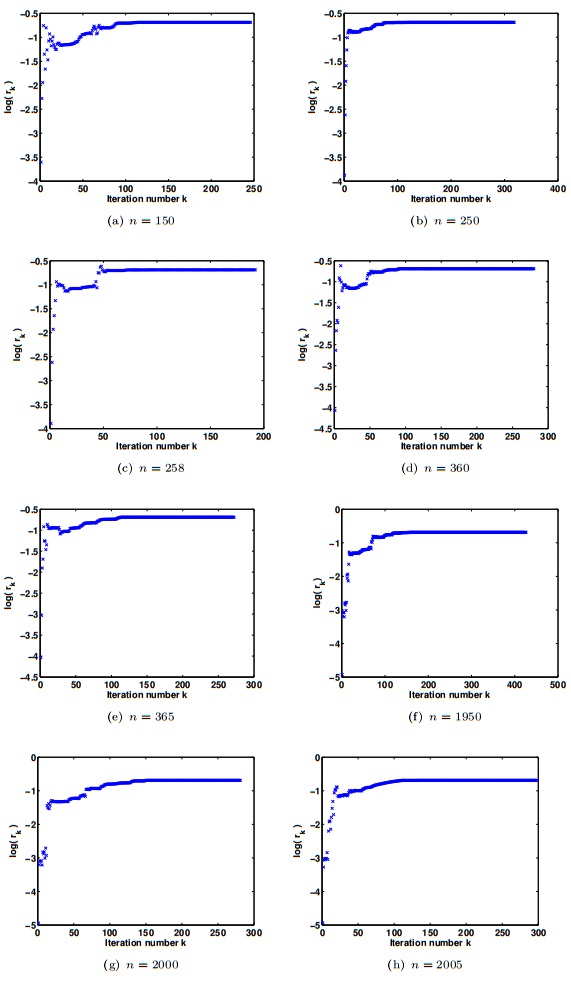
Figure 1.
The quadratic convergence behavior of the proposed algorithm
-
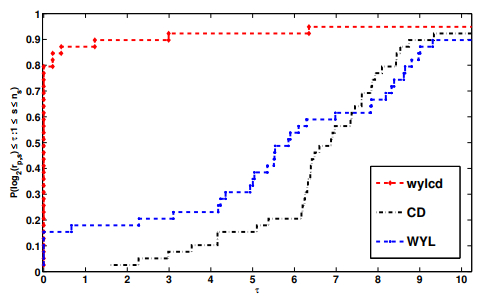
Figure 2.
Performance profile for CPU time
-
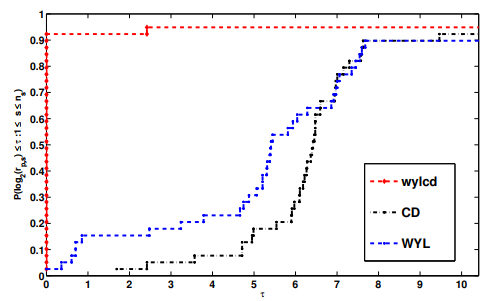
Figure 3.
Performance profile for the number of iterations.
-
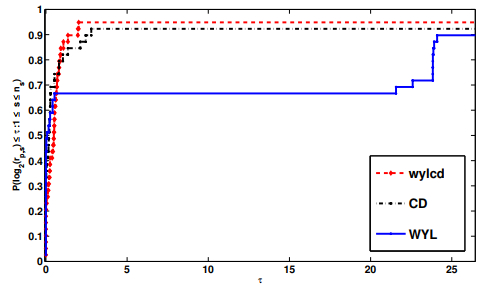
Figure 4.
Performance profile for gradient evaluations.




 DownLoad:
DownLoad: