| Citation: | Juan Liang, Guiquan Sun. EFFECT OF NONLOCAL DELAY WITH STRONG KERNEL ON VEGETATION PATTERN[J]. Journal of Applied Analysis & Computation, 2024, 14(1): 473-505. doi: 10.11948/20230290 |
EFFECT OF NONLOCAL DELAY WITH STRONG KERNEL ON VEGETATION PATTERN
-
Abstract
In order to understand the mechanism of water uptake by vegetation, we propose a vegetation-water model with nonlocal effect which is characterised by nonlocal delay with strong kernel in this paper. By mathematical analysis, the condition of producing steady pattern is obtained. Furthermore, the amplitude equation which determines the type of Turing pattern is obtained by nonlinear analysis method. The corresponding vegetation pattern and evolution process under different intensity of nonlocal effect in roots of vegetation are given by numerical simulations. The numerical results show that as intensity of nonlocal effect increases, the isolation degree of vegetation pattern increases which indicates that the robustness of the ecosystem decreases. Besides, the results reveal that with the water diffusion coefficient increases, the change of pattern structure is: stripe pattern$ \rightarrow $mixed pattern$ \rightarrow $spot pattern. Our results show the effects of diffusion coefficient and intensity of nonlocal effect on vegetation distribution, which provide theoretical basis for the study of vegetation.
-
Keywords:
- Vegetation /
- pattern /
- nonlocal delay /
- multi-scale theory
-

-
References
[1] M. Alfaro, J. Coville and G. Raoul, Travelling waves in a nonlocal reaction-diffusion equation as a model for a population structured by a space variable and a phenotypic trait, Commun. Part. Diff. Eq., 2013, 38(12), 2126–2154. doi: 10.1080/03605302.2013.828069 [2] N. Bai and R. Xu, Mathematical analysis of an HIV model with latent reservoir, delayed ctl immune response and immune impairment, Math. Biosci. Eng., 2021, 18(2), 1689–1707. doi: 10.3934/mbe.2021087 [3] J. A. Bonachela, R. M. Pringle, E. Sheffer, et al., Termite mounds can increase the robustness of dryland ecosystems to climatic change, Science, 2015, 347(6222), 651–655. doi: 10.1126/science.1261487 [4] F. Borgogno, P. Dodorico, F. Laio and L. Ridolfi, Mathmatical models of vegetation pattern formation in ecohydrology, Rev. Geophysics, 2009, 47(1), RG1005. [5] K. Boushaba and S. G. Ruan, Instability in diffusive ecological models with nonlocal delay effects, J. Math. Anal. Appl., 2001, 258, 269–286. doi: 10.1006/jmaa.2000.7381 [6] S. Chen and J. Shi, Stability and Hopf bifurcation in a diffusive logistic population model with nonlocal delay effect, J. Differ. Equations, 2012, 253(12), 3440–3470. doi: 10.1016/j.jde.2012.08.031 [7] C. Dineshkumar, R. Udhayakumar, V. Vijayakumar, et al., A note on approximate controllability for nonlocal fractional evolution stochastic integrodifferential inclusions of order $r\in(1, 2)$ with delay, Chaos Soliton. Fract., 2021, 153, 111565. doi: 10.1016/j.chaos.2021.111565 CrossRef $r\in(1, 2)$ with delay" target="_blank">Google Scholar
[8] A. Doelman and H. van der Ploeg, Homoclinic stripe patterns, SIAM J. Appl. Dyn. Syst., 2002, 1(1), 65–104. doi: 10.1137/S1111111101392831 [9] L. Eigentler and J. A. Sherratt, Analysis of a model for banded vegetation patterns in semi-arid environments with nonlocal dispersal, J. Math. Biol., 2018, 77, 739–763. doi: 10.1007/s00285-018-1233-y [10] M. Fuentes, M. Kuperman and V. Kenkre, Nonlocal interaction effects on pattern formation in population dynamics, Theor. Popul. Biol., 2003, 91(15), 158104. [11] S. Getzin, H. Yizhaq, B. Belld, et al., Discovery of fairy circles in Australia supports self-organization theory, P. Natl. Acad. Sci. USA, 2016, 113(13), 3551–3556. doi: 10.1073/pnas.1522130113 [12] E. Gilad, J. von Hardenberg, A. Provenzale, et al., A mathematical model of plants as ecosystem engineers, J. Theor. Biol., 2007, 244(4), 680–691. doi: 10.1016/j.jtbi.2006.08.006 [13] S. Gourley, M. A. Chaplain and F. Davidson, Spatio-temporal pattern formation in a nonlocal reaction-diffusion equation, Dynam. Syst., 2001, 16(2), 173–192. doi: 10.1080/14689360116914 [14] S. A. Gourley and S. Ruan, Spatio-temporal delays in a nutrient-plankton model on a finite domain: Linear stability and bifurcations, Appl. Math. Comput., 2003, 145(2–3), 391–412. [15] S. A. Gourley and J. W. H. So, Dynamics of a food-limited population model incorporating nonlocal delays on a finite domain, J. Math. Biol., 2002, 44, 49–78. doi: 10.1007/s002850100109 [16] K. Gowda, H. Riecke and M. Silber, Transitions between patterned states in vegetation models for semiarid ecosystems, Phys. Rev. E, 2014, 89(2), 022701. [17] S. J. Guo, Stability and bifurcation in a reaction-diffusion model with nonlocal delay effect, J. Differ. Equations, 2015, 259(4), 1409–1448. doi: 10.1016/j.jde.2015.03.006 [18] S. J. Guo and S. L. Yan, Hopf bifurcation in a diffusive Lotka-Volterra type system with nonlocal delay effect, J. Differ. Equations, 2016, 260(1), 781–817. doi: 10.1016/j.jde.2015.09.031 [19] S. J. Guo and J. Zimmer, Stability of travelling wavefronts in discrete reaction-diffusion equations with nonlocal delay effects, Nonlinearity, 2015, 28(2), 463–492. doi: 10.1088/0951-7715/28/2/463 [20] Z. G. Guo, G. Q. Sun, Z. Wang, et al., Spatial dynamics of an epidemic model with nonlocal infection, Appl. Math. Comput., 2020, 377, 125158. [21] B. S. Han and Z. C. Wang, Turing patterns of a Lotka-Volterra competitive system with nonlocal delay, Int. J. Bifurcat. Chaos, 2018, 28(7), 1830021. doi: 10.1142/S0218127418300215 [22] R. HilleRisLambers, M. Rietkerk, F. van den Bosch, et al., Vegetation pattern formation in semi-arid grazing systems, Ecology, 2001, 82(1), 50–61. doi: 10.1890/0012-9658(2001)082[0050:VPFISA]2.0.CO;2 [23] L. F. Hou, S. P. Gao and G. Q. Sun, Two types of fairy circles coexist in a vegetation-water model, Nonlinear Dynam., 2023, 111(8), 7883–7898. doi: 10.1007/s11071-022-08197-6 [24] L. F. Hou, G. Q. Sun and M. Perc, The impact of heterogeneous human activity on vegetation patterns in arid environments, Commun. Nonlinear Sci., 2023, 126, 107461. doi: 10.1016/j.cnsns.2023.107461 [25] B. J. Kealy and D. J. Wollkind, A nonlinear stability analysis of vegetative turing pattern formation for an interaction-diffusion plant-surface water model system in an arid flat environment, B. Math. Biol., 2012, 74(4), 803–833. doi: 10.1007/s11538-011-9688-7 [26] S. K$\acute{e}$fi, M. Rietkerk, C. L. Alados, et al., Spatial vegetation patterns and imminent desertification in mediterranean arid ecosystems, Nature, 2007, 449(7159), 213–217. doi: 10.1038/nature06111 [27] S. K$\acute{e}$fi, M. Rietkerk and G. G. Katul, Vegetation pattern shift as a result of rising atmospheric $CO_2$ in arid ecosystems, Theor. Popul. Biol., 2008, 74(4), 332–344. doi: 10.1016/j.tpb.2008.09.004 CrossRef $CO_2$ in arid ecosystems" target="_blank">Google Scholar
[28] S. K$\acute{e}$fi, M. Rietkerk, M. van Baalen and M. Loreau, Local facilitation, bistability and transitions in arid ecosystems, Theor. Popul. Biol., 2007, 71, 367–379. doi: 10.1016/j.tpb.2006.09.003 [29] C. A. Klausmeier, Regular and irregular patterns in semiarid vegetation, Science, 1999, 284, 1826–1828. doi: 10.1126/science.284.5421.1826 [30] A. Kletter, J. von Hardenberg, E. Meron and A. Provenzale, Patterned vegetation and rainfall intermittency, J. Theor. Biol., 2009, 256(4), 574–583. doi: 10.1016/j.jtbi.2008.10.020 [31] R. Lefever and O. Lejeune, On the origin of tiger bush, B. Math. Biol., 1997, 59, 263–294. doi: 10.1007/BF02462004 [32] O. Lejeune, M. Tildi and R. Lefever, Vegetation spots and stripes: Dissipative structures in arid landscapes, Int. J. Quantum Chem., 2004, 98(2), 261–271. doi: 10.1002/qua.10878 [33] H. J. Li, W. Xu, S. Song, et al., The dynamics of epidemic spreading on signed networks, Chaos Soliton. Fract., 2021, 151, 111294. doi: 10.1016/j.chaos.2021.111294 [34] J. Li, G. Q. Sun and Z. G. Guo, Bifurcation analysis of an extended Klausmeier-Gray-Scott model with infiltration delay, Stud. Appl. Math., 2022, 148, 1519–1542. doi: 10.1111/sapm.12482 [35] J. Li, G. Q. Sun and Z. Jin, Interactions of time delay and spatial diffusion induce the periodic oscillation of the vegetation system, Discre. Cont. Dyn. -B, 2022, 27, 2147–2172. [36] W. T. Li, G. Lin, C. Ma and F. Y. Yang, Traveling wave solutions of a nonlocal delayed SIR model without outbreak threshold, Discre. Cont. Dyn. -B, 2014, 19(2), 467–484. [37] J. Liang, C. liu, G. Q. Sun, et al., Nonlocal interactions between vegetation induce spatial patterning, Appl. Math. Comput., 2022, 428, 127061. [38] G. Lin and W. T. Li, Bistable wavefronts in a diffusive and competitive Lotka-Volterra type system with nonlocal delays, J. Differ. Equations, 2008, 244(3), 487–513. doi: 10.1016/j.jde.2007.10.019 [39] G. Lin and S. G. Ruan, Traveling wave solutions for delayed reaction-diffusion systems and applications to diffusive Lotka-Volterra competition models with distributed delays, J. Dyn. Differ. Equ., 2014, 26(3), 583–605. doi: 10.1007/s10884-014-9355-4 [40] G. Y. Lv and M. X. Wang, Traveling wave front and stability as planar wave of reaction diffusion equations with nonlocal delays, Z. Angew. Math. Phys., 2013, 64(4), 1005–1023. doi: 10.1007/s00033-012-0285-x [41] R. M. May, Thresholds and breakpoints in ecosystems with a multiplicity of stable states, Nature, 1977, 269, 471–477. doi: 10.1038/269471a0 [42] S. M. Merchant and W. Nagata, Instabilities and spatiotemporal patterns behind predator invasions with nonlocal prey competition, Theor. Popul. Biol., 2011, 80(4), 289–297. doi: 10.1016/j.tpb.2011.10.001 [43] F. I. Pugnaire and M. T. Luque, Changes in plant interactions along a gradient of environmental stress, Oikos, 2001, 93(1), 42–49. doi: 10.1034/j.1600-0706.2001.930104.x [44] J. A. Sherratt, An analysis of vegetation stripe formation in semi-arid landscapes, J. Math. Biol., 2005, 51, 183–197. doi: 10.1007/s00285-005-0319-5 [45] J. P. Shi, Z. F. Xie and K. Little, Cross-diddusion induce instability and stability in reaction-diffusion system, J. Appl. Anal. Comput., 2011, 1(1), 95–119. [46] E. Siero, A. Doelman, M. B. Eppinga, et al., Striped pattern selection by advective reaction-diffusion systems: Resilience of banded vegetation on slopes, Chaos, 2015, 25(3), 036411. doi: 10.1063/1.4914450 [47] H. T. Song, G. H. Fan, S. Zhao, et al., Forecast of the COVID–19 trend in India: A simple modelling approach, Math. Biosci. Eng., 2021, 18(6), 9775–9786. doi: 10.3934/mbe.2021479 [48] Y. L. Song, S. H. Wu and H. Wang, Spatiotemporal dynamics in the single population model with memory-based diffusion and nonlocal effect, J. Differ. Equations, 2019, 267(11), 6316–6351. doi: 10.1016/j.jde.2019.06.025 [49] M. J. Steinbauer, J. A. Grytnes, G. Jurasinski, et al., Accelerated increase in plant species richness on mountain summits is linked to warming, Nature, 2018, 556, 231–250. doi: 10.1038/s41586-018-0005-6 [50] G. Q. Sun, M. Jusup, Z. Jin, et al., Pattern transitions in spatial epidemics: Mechanisms and emergent properties, Phys. Life Rev., 2016, 19, 43–73. doi: 10.1016/j.plrev.2016.08.002 [51] G. Q. Sun, L. Li, J. Li, et al., Impacts of climate change on vegetation pattern: Mathematical modelling and data analysis, Phys. Life Rev., 2022, 43, 239–270. doi: 10.1016/j.plrev.2022.09.005 [52] G. Q. Sun, C. H. Wang, L. L. Chang, et al., Effects of feedback regulation on vegetation patterns in semi-arid environments, Appl. Math. Model., 2018, 61, 200–215. doi: 10.1016/j.apm.2018.04.010 [53] G. Q. Sun, H. T. Zhang, Y. L. Song, et al., Dynamic analysis of a plant-water model with spatial diffusion, J. Differ. Equations, 2022, 329, 395–430. doi: 10.1016/j.jde.2022.05.009 [54] Q. L. Tang, J. Ge and Z. G. Lin, An SEI-SI avian-human influenza model with diffusion and nonlocal delay, Appl. Math. Comput., 2014, 247, 753–761. [55] S. Thompson, G. Katul, J. Terborgh and P. Alvarez-Loayza, Spatial organization of vegetation arising from non-local excitation with local inhibition in tropical rainforests, Physica D, 2009, 238, 1061–1067. doi: 10.1016/j.physd.2009.03.004 [56] C. J. Tucker, I. Y. Fungt, C. D. Keeling and R. H. Gammon, Relationship between atmospheric $CO_2$ variations and a satellite-derived vegetation index, Nature, 1986, 319, 195–198. doi: 10.1038/319195a0 CrossRef $CO_2$ variations and a satellite-derived vegetation index" target="_blank">Google Scholar
[57] J. von Hardenberg, E. Meron, M. Shachak and Y. Zarmi, Diversity of vegetation patterns and desertification, Phys. Rev. Lett., 2001, 87(19), 198101. doi: 10.1103/PhysRevLett.87.198101 [58] J. van de Koppel, M. Rietkerk and F. J. Weissing, Catastrophic vegetation shifts and soil degradation in terrestrial grazing systems, Trends Ecol. Evol., 1997, 12, 352–356. doi: 10.1016/S0169-5347(97)01133-6 [59] J. B. Wang, W. T. Li and F. Y. Yang, Traveling waves in a nonlocal dispersal SIR model with nonlocal delayed transmission, Commun. Nonlinear Sci., 2015, 27(1–3), 136–152. doi: 10.1016/j.cnsns.2015.03.005 [60] M. X. Wang and G. Lv, Entire solutions of a diffusive and competitive Lotka-Volterra type system with nonlocal delays, Nonlinearity, 2010, 23(7), 1609–1630. doi: 10.1088/0951-7715/23/7/005 [61] Z. C. Wang, W. T. Li and S. G. Ruan, Existence and stability of traveling wave fronts in reaction advection diffusion equations with nonlocal delay, J. Differ. Equations, 2007, 238(1), 153–200. doi: 10.1016/j.jde.2007.03.025 [62] Z. C. Wang, W. T. Li and S. G. Ruan, Traveling fronts in monostable equations with nonlocal delayed effects, J. Dyn. Differ. Equ., 2008, 20(3), 573–607. doi: 10.1007/s10884-008-9103-8 [63] Z. C. Wang, W. T. Li and S. G. Ruan, Entire solutions in bistable reaction-diffusion equations with nonlocal delayed nonlinearity, Tra. Amer. Soc., 2009, 361(4), 2047–2084. [64] S. Wu, J. Shi and B. Wu, Global existence of solutions and uniform persistence of a diffusive predator-prey model with prey-taxis, J. Differ. Equations, 2016, 26(7), 5847–5874. [65] R. Xu, M. A. J. Chaplain and F. A. Davidson, Travelling wave and covetgence in stage-structured reaction-diffusion competitive models with nonlocal delays, Chaos Soliton. Fract., 2006, 30, 974–992. doi: 10.1016/j.chaos.2005.09.022 [66] Q. Xue, C. Liu, L. Li, et al., Interactions of diffusion and nonlocal delay give rise to vegetation patterns in semi-arid environments, Appl. Math. Comput., 2021, 399, 126038. [67] S. Zaytseva, J. P. Shi and L. B Shaw, Model of pattern formation in marsh ecosystems with nonlocal interactions, J. Math. Biol., 2019, 86, 655–686. [68] L. Zhang and Z. G. Lin, A Höllings type II prey-predator model with stage structure and nonlocal delay, Appl. Math. Comput., 2011, 217(10), 5000–5010. [69] J. D. Zhao and T. H. Zhang, Dynamics of two predator-prey models with power law pelation, J. Appl. Anal. Comput., 2023, 13(1), 233–248. -
-
-
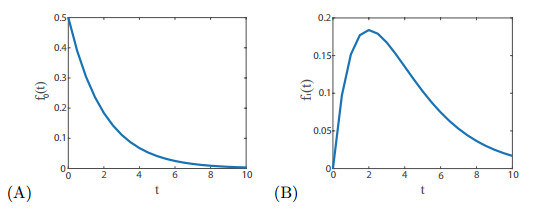
Figure 1.
Image of the weak kernel (A) and strong kernel (B) over time.
-
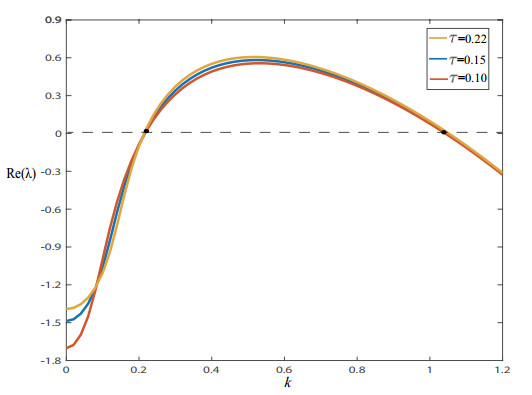
Figure 2.
Dispersion relation of system (2.7). In the case of fixed other parameters:
$ \eta=2.6, \gamma=1.2, \beta=30 $ $ \tau $ $ \tau $ $ k $ $ Re(\lambda)<0 $ -
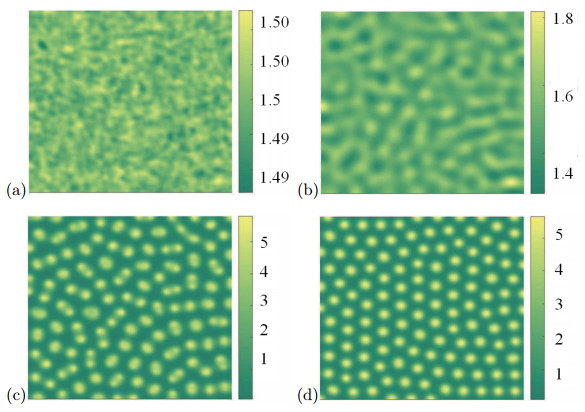
Figure 3.
When
$ \tau=0.22 $ $ \eta=2.6, \gamma=1.2, \beta=30 $ $ (a)\rightarrow (b)\rightarrow (c)\rightarrow (d). $ -
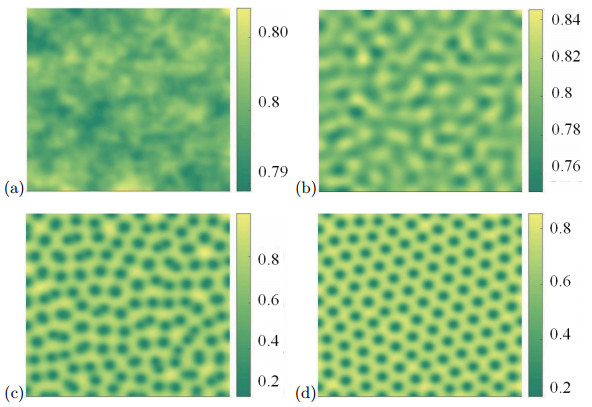
Figure 4.
When
$ \tau=0.22 $ $ \eta=2.6, \gamma=1.2, \beta=30 $ $ (a)\rightarrow (b)\rightarrow (c)\rightarrow (d). $ -
Figure 5.
Different
$ \beta $ $ \beta $ $ \eta=2.6, \gamma=1.2, \tau=0.22 $ $ (a)\ \beta=8; (b)\ \beta=10; (c)\ \beta=12; (d)\ \beta=14 $ -
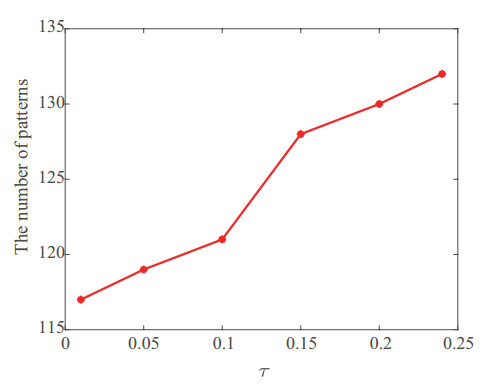
Figure 6.
The number of spot patterns at different parameter
$ \tau $ $ \eta=2.6, \gamma=1.2, \beta=30 $ -
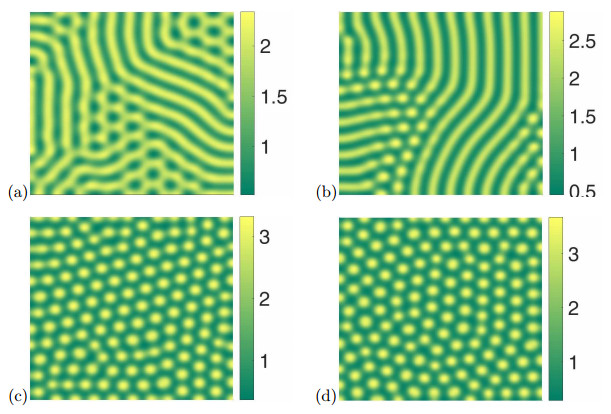
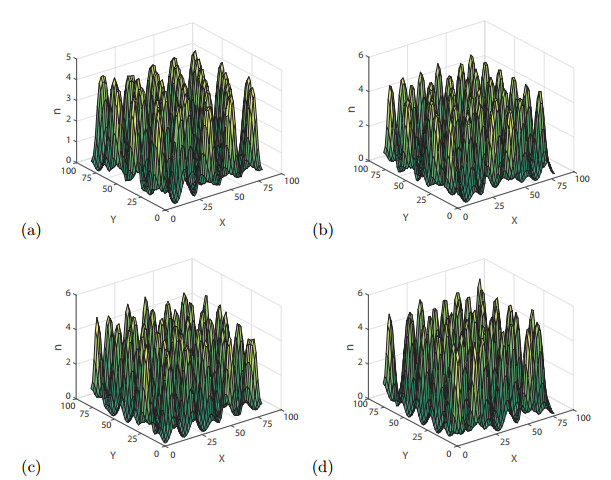
Figure 7.
Different
$ \tau $ $ \eta=2.6, \gamma=1.2, \beta=30 $ $ (a)\ \tau=0.01; (b)\ \tau=0.1; (c)\ \tau=0.15; (d)\ \tau=0.24 $ -
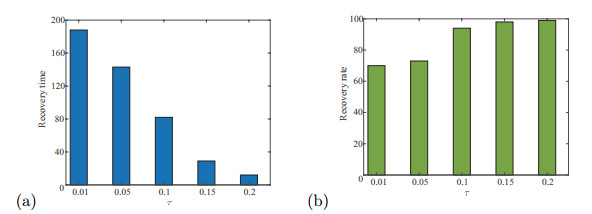
Figure 8.
Different
$ \tau $ $ \eta=2.6, \gamma=1.2, \beta=30 $ $ \tau $ $ \tau $




 DownLoad:
DownLoad: