| Citation: | Yanli Tang, Feng Li. MULTIPLE STABLE STATES FOR A CLASS OF PREDATOR-PREY SYSTEMS WITH TWO HARVESTING RATES[J]. Journal of Applied Analysis & Computation, 2024, 14(1): 506-514. doi: 10.11948/20230295 |
MULTIPLE STABLE STATES FOR A CLASS OF PREDATOR-PREY SYSTEMS WITH TWO HARVESTING RATES
-
Abstract
In this paper, a class of predator-prey systems with two harvesting rates is studied, multiple limit cycles can be obtained by hopf bifurcation, and the Hopf cyclicity at the origin is $ 4 $. Multiple stable states can coexist in the predator-prey systems with two harvesting rates. Then by using Poincare-Bendixson theorem and Dulac discriminant method, existence and non-existence conditions of limit cycles are obtained.
-
Keywords:
- Predator-prey system /
- limit cycle /
- Dulac function
-

-
References
[1] A. E. Aroudi, J. Huang, M. S. Al-Numay and Z. Li, On the coexistence of multiple limit cycles in H-bridge wireless power transfer systems with zero current switching control, IEEE Tran. Circ and Sys., 2020, 67, 1729–1739. [2] S. Beregi, D. Takacs and G. Stepan, Bifurcation analysis of wheel shimmy with non-smooth effects and time delay in the tyre-ground contact, Nonlinear Dyn., 2019, 98, 841–858. doi: 10.1007/s11071-019-05123-1 [3] L. A. Cherkas, Conditions for a Liénard equation to have a centre, Differ. Equ., 1976, 12, 201–206. [4] A. Gasull and J. Torregrosa, Center problem for several differential equations via Cherkas' method, J. Math. Anal. Appl., 1998, 228, 322–343. doi: 10.1006/jmaa.1998.6112 [5] E. D. Han, W. W. Zheng and L. G. Luo, Weak focus and Limit cycles of a predator-prey system with Harvesting rate, J. Biomathematics, 2012, 3, 447–454. [6] M. Han, Bifurcation Theory of Limit Cycles, Science Press, Beijing, 2013. [7] C. S. Holling, The functional response of predators to prey density and its role in mimicry and population regulation, Mem. Entomol. Soc. Can., 97, 1965, 5–60. [8] A. T. Keong, H. M. Safuan and K. Jacob, Dynamical Behaviours of Prey-predator Fishery Modelwith Harvesting Affected by Toxic Substances, Mathematika, 2018, 34, 143–151. [9] F. Li, Y. Liu, Y. Liu and P. Yu, Bi-center problem and bifurcation of limit cycles from nilpotent singular points in $Z_2$-equivariant cubic vector fields, J. Differ. Equ., 2018, 265, 4965–4992. doi: 10.1016/j.jde.2018.06.027 CrossRef $Z_2$-equivariant cubic vector fields" target="_blank">Google Scholar
[10] F. Li, Y. Liu, Y. Liu and P. Yu, Complex isochronous centers and linearization transformations for cubic $Z_2$-equivariant planar systems, J. Differ. Equ., 2020, 268, 3819–3847. doi: 10.1016/j.jde.2019.10.011 CrossRef $Z_2$-equivariant planar systems" target="_blank">Google Scholar
[11] F. Li, Y. Liu, Y. Tian and P. Yu, Integrability and linearizability of cubic $Z_2$ systems with non-resonant singular points, J. Differ. Equ., 2020, 269, 9026–9049. doi: 10.1016/j.jde.2020.06.036 CrossRef $Z_2$ systems with non-resonant singular points" target="_blank">Google Scholar
[12] F. Li, Y. Liu, P. Yu and J. Wang, Complex integrability and linearizability of cubic $Z_2$-equivariant systems with two 1: q resonant singular points, J. Differ. Equ., 2021, 300, 786–813. doi: 10.1016/j.jde.2021.08.015 CrossRef $Z_2$-equivariant systems with two 1: q resonant singular points" target="_blank">Google Scholar
[13] N. Li, M. Han and V. G. Romanovski, Cyclicity of some Liénard systems, Commun. Pure Appl. Anal., 2015, 14, 2127–2150. doi: 10.3934/cpaa.2015.14.2127 [14] X. Li and M. Zhang, Integrability and multiple limit cycles in a predator-prey system with fear effect, J. Function Spaces, 2019, 2019. [15] X. Y. Meng, N. N. Qin and H. F. Huo, Dynamics analysis of a predator-prey system with harvesting prey and disease in prey species, J. Biological Dynamics, 2018, 12, 342–374. doi: 10.1080/17513758.2018.1454515 [16] S. Sarwardi, M. Haque and E. Venturino, Global stability and persistence in LGHolling type Ⅱ diseased predator ecosystems, J. Biol. Phys., 2011, 37, 91–106. doi: 10.1007/s10867-010-9201-9 [17] S. M. Shang and Y. Tian, Multiplicity and Stability of Equilibrium States of Three-Dimensional Nonlinear System, J. Nonl. Mod. Anal., 2019, 1, 595–604. [18] Z. G. Shi and C. Q. Wu, The qualitative analysis of a predator-prey system with constant-rate prey harvesting under type-Ⅳ functional response, J. Fuzhou University, 2008, 3, 327–330. [19] D. Wei, Y. Zhu, T. Jiang, A. Yin and W. Zhai, Multiple limit cycles shimmy of the dual-front axle steering heavy truck based on bisectional road, ASME. J. Comput. Nonlinear Dyn., 2019, 5, 051005. [20] X. Zhang, Z. Jin and P. Yu, Bifurcation of multiple limit cycles in an epidemic model on adaptive networks, Int. J. Bifurcation and Chaos, 2019, 29, 1950096. doi: 10.1142/S0218127419500962 [21] R. D. Zhao and Q. M. Liu, Dynamical Analysis of a Delayed SIQS Epidemic Model on Scale-Free Networks, J. Nonl. Mod. Anal., 2021, 3, 561–576. -
-
-
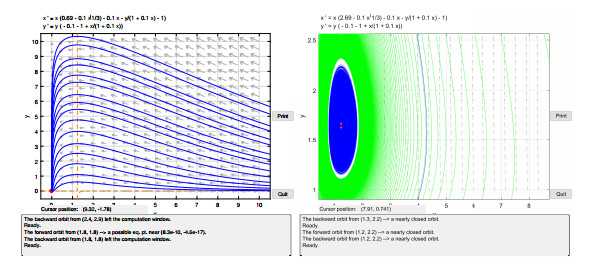
Figure 1.
Phase portrait of system (1.1) showing that there is no other singular point and limit cycle when
$ a-eq_1\leq 0 $ $ a-eq_1> 0 $




 DownLoad:
DownLoad: