| Citation: | Bingfeng Zhang, Fu Zheng, Yong He. UNIFORMLY EXPONENTIALLY STABLE APPROXIMATION FOR THE TRANSMISSION LINE WITH VARIABLE COEFFICIENTS AND ITS APPLICATION[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 2228-2256. doi: 10.11948/20230361 |
UNIFORMLY EXPONENTIALLY STABLE APPROXIMATION FOR THE TRANSMISSION LINE WITH VARIABLE COEFFICIENTS AND ITS APPLICATION
-
Abstract
We analyze an ideal transmission line, which is defined by the telegraph equation with variable coefficients, from the perspectives of numerical analysis and control theory in this note. Because the spatially semi-discrete scheme of the original system is insufficient for discussing uniform exponential stability, we apply a similar transform to the continuous system and produce an intermediate system that may be easily analyzed. To begin, we discuss uniform exponential stability for the intermediate system using an so called average central-difference semi-discrete scheme and the direct Lyapunov function approach. The proof is the same as in the continuous case. The Trotter-Kato Theorem is used to demonstrate the stability and consistency of numerical approximation scheme. Finally, we propose a semi-discrete strategy for the original system through an inverse transform. All results on intermediate system are then translated into the original system. The numerical state reconstruction problem is addressed as an essential application of the main results. Furthermore, several numerical simulations are used to validate the effectiveness of the numerical approximating algorithms.
-

-
References
[1] H. T. Banks, K. Ito and C. Wang, Exponentially stable approximations of weakly damped wave equations, in: W. Desch, F. Kappel, K. Kunisch (eds.), Estimation and Control of Distributed Parameter Systems, Birkhauser, Basel, 1991, 1–33. [2] K. J. Engel, R. Nagel, One-Parameter Semigroups for Linear Evolution Equations, Springer-Verlag, New York, 2000. [3] S. Ervedoza, A. Marica and E. Zuazua, Numerical meshes ensuring uniform observability of 1D waves: Construction and analysis, IMA J. Numer. Anal., 2016, 36, 503–542. doi: 10.1093/imanum/drv026 [4] F. Gao and C. M. Chi, Unconditionally stable difference schemes for a one-space-dimensional linear hyperbolic equation, Appl. Math. Comput., 2007, 187, 1272–1276. [5] R. Glowinski, C. H. Li and J. L. Lions, A numerical approach to the exact boundary controllability of the wave equation. (Ⅰ). Dirichlet controls: Description of the numerical methods, Japan J. Appl. Math., 1990, 103, 1–76. [6] G. Golo, et al., Hamiltonian discretization of boundary control systems, Automatica, 2004, 40, 757–771. doi: 10.1016/j.automatica.2003.12.017 [7] B. Z. Guo and B. B. Xu, A semi-discrete finite difference method to uniform stabilization of wave equation with local viscosity, IFAC Journal of Systems and Control, 2020, 13, 101000. [8] B. Z. Guo and F. Zheng, Frequency energy multiplier approach to uniform exponential stability analysis of semi-discrete scheme for a Schrödinger equation under boundary feedback, Preprint, Hainan University, 2022. [9] C. Harkort and J. Deutscher, Stability and passivity preserving Petrov-Galerkin approximation of linear infinite-dimensional systems, Automatica, 2012, 48, 1347–1352. doi: 10.1016/j.automatica.2012.04.010 [10] W. W. Hu, et al., Hybrid domain decomposition filters for advection-diffusion PDEs with mobile sensors, Automatica, 2022, 138, 110109. doi: 10.1016/j.automatica.2021.110109 [11] J. A. Infante and E. Zuazua, Boundary observability for the space semi-discretizations of the 1-D wave equation, Mathematical Modelling and Numerical Analysis, 1999, 33, 407–438. doi: 10.1051/m2an:1999123 [12] K. Ito and F. Kappel, The Trotter-Kato theorem and approximation of PDEs, Mathematics of Computation, 1998, 221, 21–44. [13] B. Jacob and H. Zwart, Linear Port-Hamiltonian System on Infinite-dimensional Space, Springer-Verlag, Basel, 2012. [14] R. Kress, Numerical Analysis, Graduate Texts in Mathematics 181, Springer-Verlag, New York, 1998. [15] M. Krstic and A. Smyshlyaev, Boundary Control of PDEs: A Course on Backstepping Designs, SIAM, Philadelphia, 2008. [16] S. X. Li and Y. K. Wu, Energy-preserving mixed finite element methods for the elastic wave equation, Appl. Math. Comput., 2022, 422, 126963. [17] Y. P. Li, Y. L. Jiang and P. Yang, Model order reduction of port-Hamiltonian systems with inhomogeneous initial conditions via approximate finite-time Gramians, Appl. Math. Comput., 2022, 422, 126959. [18] J. K. Liu and B. Z. Guo, A new semi-discretized order reduction finite difference scheme for uniform approximation of 1-D wave equation, SIAM J. Control Optim., 2020, 58, 2256–2287. doi: 10.1137/19M1246535 [19] X. Q. Luo and Q. K. Du, An unconditionally stable fourth-order method for telegraph equation based on Hermite interpolation, Appl. Math. Comput., 2013, 219, 8237–8246. [20] A. Macchelli, Energy shaping of distributed parameter port-Hamiltonian systems based on finite element approximation, Syst. Control Lett., 2011, 60, 579–589. doi: 10.1016/j.sysconle.2011.04.016 [21] A. Macchelli, Y. L. Gorrec, Y. Wu and H. Ramírez, Energy-based control of a wave equation with boundary anti-damping, IFAC-PapersOnLine, 2020, 53, 7740–7745. doi: 10.1016/j.ifacol.2020.12.1527 [22] A. Marica and E. Zuazua, Boundary stabilization of numerical approximations of the 1-D variable coefficients wave equation a numerical viscosity approach, in: R. Hoppe (Eds.), Optimization with PDE Constraints, Lecture Notes in Computational Science and Engineering 101, Springer, Switzerland, 2014, 285–324. [23] S. Micu and C. Castro, Boundary controllability of a linear semi-discrete 1-D wave equation derived from a mixed finite element method, Numerische Mathematik, 2006, 102, 413–462. doi: 10.1007/s00211-005-0651-0 [24] A. Münch and P. F. Pazoto, Uniform stabilization of a viscous numerical approximation for a locally damped wave equation, ESAIM COCV., 2007, 13, 265–293. doi: 10.1051/cocv:2007009 [25] M. Negreanu, Convergence of a semidiscrete two-grid algorithm for the controllability of the 1-D wave equation, SIAM Journal on Numerical Analysis, 2008, 46, 3233–3263. doi: 10.1137/06064915X [26] K. Ramdani and M. Tucsnak and G. Weiss, Recovering the initial state of an infinite-dimensional system using observers, Automatica, 2010, 46, 1616–1625. doi: 10.1016/j.automatica.2010.06.032 [27] M. Seslija, A. van der Schaft and J. M. Scherpen, Discrete exterior geometry approach to structure preserving discretization of distributed-parameter port-Hamiltonian systems, Geom. Phys., 2012, 62, 1509–1531. [28] L. T. Tebou and E. ZuaZua, Uniform boundary stabilization of the finite difference space discretization of the 1-D wave equation, Advances in Computational Mathematics, 2007, 26, 337–365. [29] V. Trenchant, et al., Finite differences on staggered grids preserving the port Hamiltonian structure with application to an acoustic duct, Journal of Computational Physics, 2018, 373, 673–697. [30] M. Tucsnak and G. Weiss, Observation and Control for Operator Semigroups, Birkhauser, Basel, 2009. [31] M. Zhang, et al., Discontinuous Galerkin method for the diffusive-viscous wave equation, Applied Numerical Mathematics, 2023, 183, 118–139. [32] F. Zheng and H. Zhou, State reconstruction of the wave equation with general viscosity and non-collocated observation and control, J. Math. Anal. Appl., 2021, 502, 125257. [33] F. Zheng, et al., The exponential stabilization of a heat-wave coupled system and its approximation, J. Math. Anal. Appl., 2022, 126927. [34] E. Zuazua, Propagation, observation, and control of waves approximated by finite difference methods, SIAM Rev., 2005, 47, 197–243. -
-
-
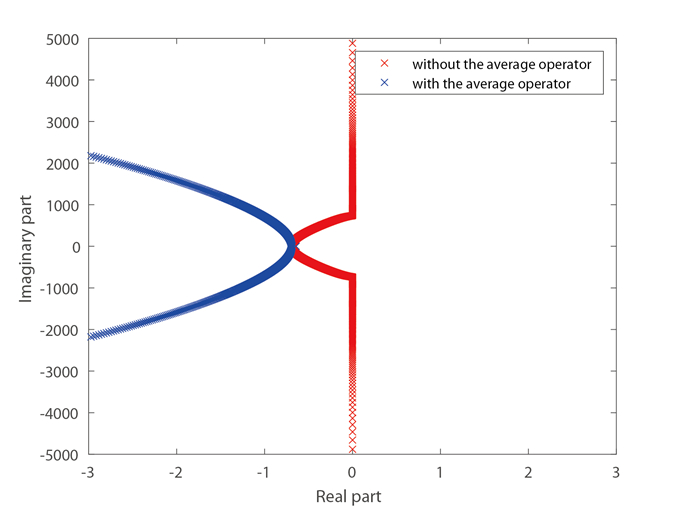
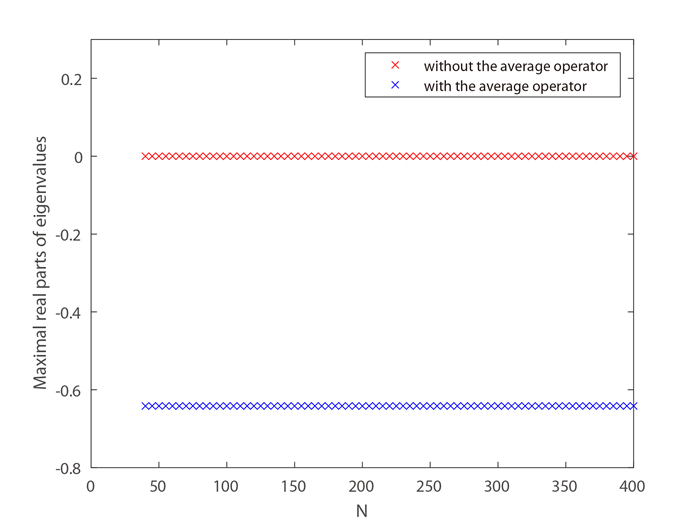
Figure 1.
Maximal real parts of eigenvalues of the semi-discrete schemes
-
Figure 2.
Maximal real parts of eigenvalues of the semi-discrete scheme with
$ N=500 $ -
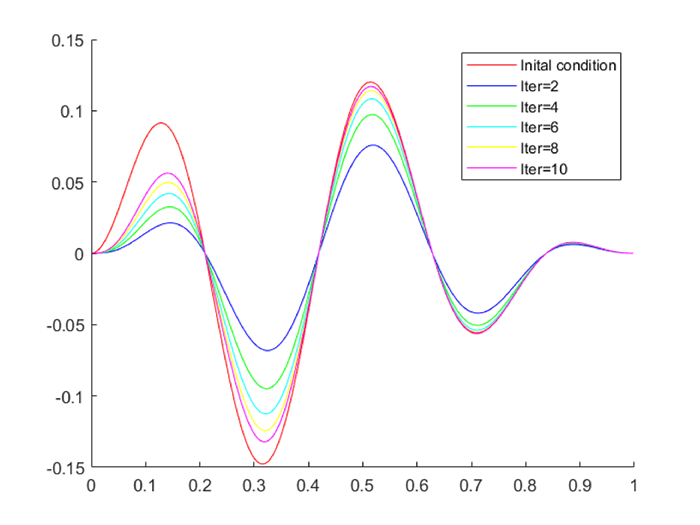
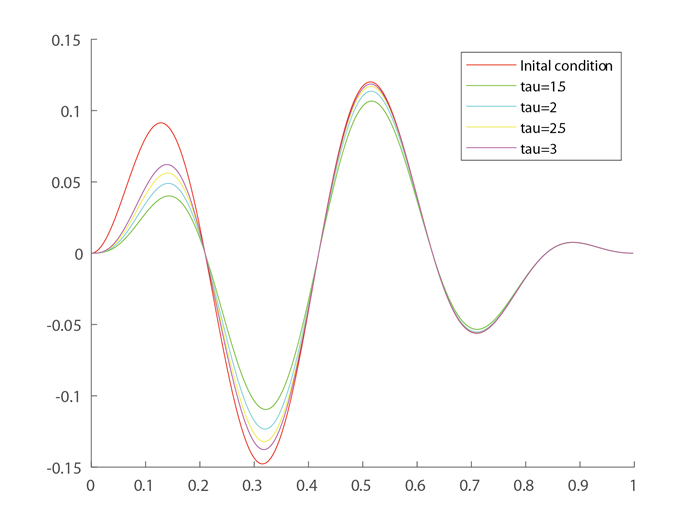
Figure 3.
Reconstruction of
$V_0$ -
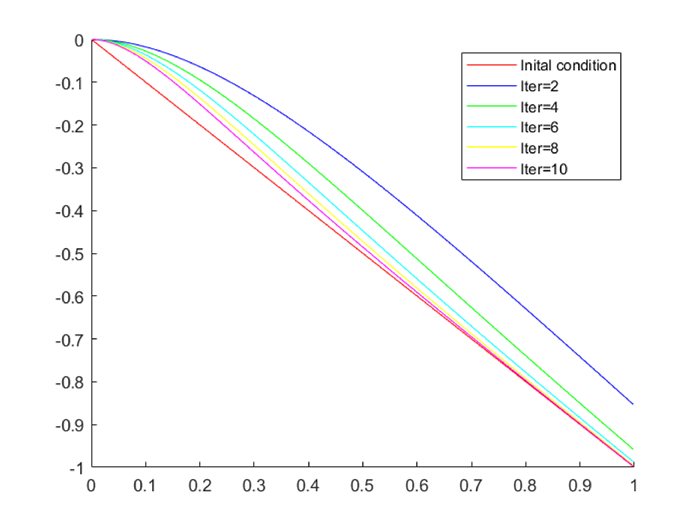
Figure 4.
Reconstruction of
$I_0$ -
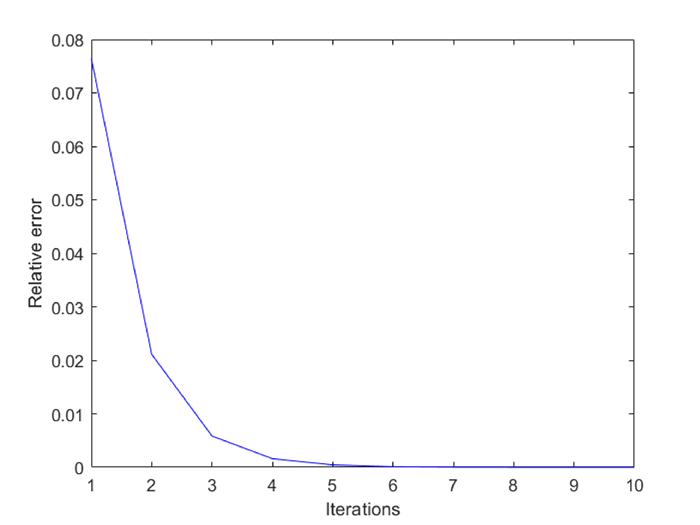
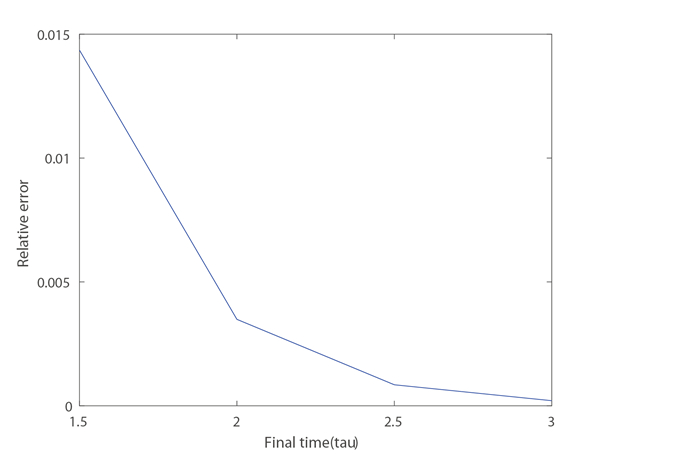
Figure 5.
Relative error made after
$n$ -
Figure 6.
Reconstruction of
$ V_0 $ -
Figure 7.
Relative error with respect to
$ \tau $




 DownLoad:
DownLoad: