| Citation: | Xiaoyu Xu, Junmin Yang, Tong Han. THE NUMBER OF LIMIT CYCLES NEAR A DOUBLE HOMOCLINIC LOOP FOR A NEAR-HAMILTONIAN SYSTEM[J]. Journal of Applied Analysis & Computation, 2024, 14(2): 1111-1132. doi: 10.11948/20230387 |
THE NUMBER OF LIMIT CYCLES NEAR A DOUBLE HOMOCLINIC LOOP FOR A NEAR-HAMILTONIAN SYSTEM
-
Abstract
In this paper, for a general near-Hamiltonian system we study the number and distributions of limit cycles near a double homoclinic loop. For a cubic Hamiltonian system with general polynomial perturbations, we obtain a lower bound of the maximum number of limit cycles near a double homoclinic loop.
-
Keywords:
- Limit cycle /
- Melnikov function /
- homoclinic loop /
- bifurcation
-

-
References
[1] V. I. Arnold, Loss of stability of self-induced oscillations near resonance, and versal deformations of equivariant vector fields, Funct. Anal. Appl., 1977, 11, 85–92. doi: 10.1007/BF01081886 [2] W. Geng, M. Han, Y. Tian and A. Ke, Heteroclinic bifurcation of limit cycles in perturbed cubic Hamiltonian systems by higher-order analysis, J. Differential Equations, 2023, 357, 412–435. doi: 10.1016/j.jde.2023.02.027 [3] W. Geng and Y. Tian, Bifurcation of limit cycles near heteroclinic loops in near-Hamiltonian systems, Commun. Nonlinear Sci. Numer. Simul., 2021, 95(12), 105666. [4] M. Han, On Hopf cyclicity of planar systems, J. Math. Anal. Appl., 2000, 245(2), 404–422. doi: 10.1006/jmaa.2000.6758 [5] M. Han, Asymptotic expansions of Melnikov functions and limit cycle bifurcations, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2012, 22(12), 1250296, 30pp. [6] M. Han and J. Chen, On the number of limit cycles in double homoclinic bifurcations, Sci. China Ser. A, 2000, 43(9), 914–928. doi: 10.1007/BF02879797 [7] M. Han, J. Yang and J. Li, General study on limit cycle bifurcation near a double homoclinic loop, J. Differential Equations, 2023, 347, 1–23. doi: 10.1016/j.jde.2022.11.031 [8] M. Han, J. Yang, A.-A. Tarţa and Y. Gao, Limit cycles near homoclinic and heteroclinic loops, J. Dynam. Differential Equations, 2008, 20, 923–944. doi: 10.1007/s10884-008-9108-3 [9] M. Han, J. Yang and D. Xiao, Limit cycle bifurcations near a double homoclinic loop with a nilpotent saddle, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2012, 22(8), 1250189, 33pp. [10] M. Han and Y. Ye, On the coefficients appearing in the expansion of Melnikov functions in homoclinic bifurcations, Ann. Differential Equations, 1998, 14(2), 156–162. [11] M. Han and P. Yu, Normal forms, Melnikov Functions and Bifurcations of Limit Cycles, Vol. 181 of Applied Mathematical Sciences, Springer, London, 2012. [12] M. Han, H. Zang and J. Yang, Limit cycle bifurcations by perturbing a cuspidal loop in a Hamiltonian system, J. Differential Equations, 2009, 246(1), 129–163. doi: 10.1016/j.jde.2008.06.039 [13] H. He and D. Xiao, On the global center of planar polynomial differential systems and the related problems, J. Appl. Anal. Comput., 2022, 12(3), 1141–1157. [14] D. Hilbert, Mathematical problems, Bull. Amer. Math. Soc., 1902, 8(10), 437–479. doi: 10.1090/S0002-9904-1902-00923-3 [15] W. Hou and S. Liu, Melnikov functions for a class of piecewise Hamiltonian systems, J. Nonlinear Model. and Anal., 2023, 5(1), 123–145. [16] I. D. Iliev, C. Li and J. Yu, On the cubic perturbations of the symmetric 8-loop Hamiltonian, J. Differential Equations, 2020, 269(4), 3387–3413. doi: 10.1016/j.jde.2020.03.003 [17] C. Li, Abelian integrals and limit cycles, Qual. Theory Dyn. Syst., 2012, 11(1), 111–128. doi: 10.1007/s12346-011-0051-z [18] J. Li, Hilbert's 16th problem and bifurcations of planar polynomial vector fields, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2003, 13(1), 47–106. doi: 10.1142/S0218127403006352 [19] J. Llibre and C. Valls, The 16th Hilbert problem for discontinuous piecewise linear differential systems separated by the algebraic curve $ y=x^n$, Math. Phys. Anal. Geom., 2023, 26(4), Paper No. 25, 9pp. [20] M. Mousavi and H. R. Z. Zangeneh, Limit cycle bifurcations by perturbing a Hamiltonian system with a 3-polycycle having a cusp of order one or two, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2018, 28(3), 1850038, 20pp. [21] R. Roussarie, On the number of limit cycles which appear by perturbation of separatrix loop of planar vector fields, Bol. Soc. Brasil. Mat., 1986, 17(2), 67–101. doi: 10.1007/BF02584827 [22] Y. Tian and M. Han, Hopf and homoclinic bifurcations for near-Hamiltonian systems, J. Differential Equations, 2017, 262(4), 3214–3234. doi: 10.1016/j.jde.2016.11.026 [23] L. Wei, Limit cycle bifurcations near generalized homoclinic loop in piecewise smooth systems with a cusp, Nonlinear Anal. Real World Appl., 2017, 38, 306–326. doi: 10.1016/j.nonrwa.2017.05.001 [24] L. Wei, F. Liang and S. Lu, Limit cycle bifurcations near a generalized homoclinic loop in piecewise smooth systems with a hyperbolic saddle on a switch line, Appl. Math. Comput., 2014, 243, 298–310. [25] J. Yang and M. Han, Limit cycles near a double homoclinic loop, Ann. Differential Equations, 2007, 23(4), 536–545. [26] J. Yang and L. Zhao, The perturbation of a class of hyper-elliptic Hamilton system with a double eight figure loop, Qual. Theory Dyn. Syst., 2017, 16(2), 317–360. -
-
-
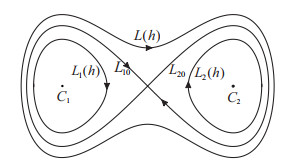
Figure 1.
The double homoclinic loop
$ L_0 $




 DownLoad:
DownLoad: