| Citation: | Dandan Zhu, Ying Xu, Xueping Li. ON A PARTIALLY DEGENERATE REACTION-ADVECTION-DIFFUSION SYSTEM WITH FREE BOUNDARY CONDITIONS[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 21-38. doi: 10.11948/20230391 |
ON A PARTIALLY DEGENERATE REACTION-ADVECTION-DIFFUSION SYSTEM WITH FREE BOUNDARY CONDITIONS
-
Abstract
A partially degenerate reaction-diffusion system with advection term and free boundary conditions is investigated in this paper. Firstly, we present a spreading-vanishing dichotomy for the asymptotic behavior of solutions of the system. Then, we obtain criteria for spreading and vanishing. Moreover, numerical simulation is given to illustrate the theoretical results.
-

-
References
[1] I. Ahn, S. Beak and Z. G. Lin, The spreading fronts of an infective environment in a man-environment-man epidemic model, Appl. Math. Model, 2016, 40, 7082–7101. doi: 10.1016/j.apm.2016.02.038 [2] J. F. Cao, Y. H. Du, F. Li and W. T. Li, The dynamics of a Fisher-KPP nonlocal diffusion model with free boundaries, J. Funct. Anal., 2019, 277, 2772–2814. doi: 10.1016/j.jfa.2019.02.013 [3] V. Capasso and L. Maddalena, Convergence to equilibrium states for a reaction-diffusion system modeling the spatial spread of a class of bacterial and viral diseases, J. Math. Biol., 1981, 13, 173–184. doi: 10.1007/BF00275212 [4] Q. L. Chen, F. Q. Li, Z. D. Teng and F. Wang, Global dynamics and asymptotic spreading speeds for a partially degenerate epidemic model with time delay and free boundaries, J. Dyn. Differential Equations, 2022, 34, 1209–1236. doi: 10.1007/s10884-020-09934-4 [5] Q. L. Chen, F. Q. Li and F. Wang, A reaction-diffusion-advection competition model with two free boundaries in heterogeneous time-periodic environment, IMA J. Appl. Math., 2017, 82, 445–470. [6] W. Choi and I. Ahn, Non-uniform dispersal of logistic population models with free boundaries in a spatially heterogeneous environment, J. Math. Anal. Appl., 2019, 479, 283–314. doi: 10.1016/j.jmaa.2019.06.027 [7] Y. H. Du and Z. G. Lin, Spreading-vanishing dichotomy in the diffusive logistic model with a free boundary, SIAM J. Math. Anal., 2010, 42, 377–405. doi: 10.1137/090771089 [8] J. Fang and X. Q. Zhao, Monotone wavefronts for partially degenerate reaction-diffusion systems, J. Diff. Eqs., 2009, 21, 663–680. doi: 10.1007/s10884-009-9152-7 [9] H. Gu, Z. G. Lin and B. D. Lou, Long time behavior of solutions of a diffusion-advection logistic model with free boundaries, Appl. Math. Lett., 2014, 37, 49–53. doi: 10.1016/j.aml.2014.05.015 [10] H. Gu, Z. G. Lin and B. D. Lou, Different asymptotic spreading speeds induced by advection in a diffusion problem with free boundaries, Proc. Amer. Math. Soc., 2015, 143, 1109–1117. [11] H. Gu, B. D. Lou and M. L. Zhou, Long time behavior of solutions of Fisher-KPP equation with advection and free boundaries, J. Funct. Anal., 2015, 269, 1714–1768. doi: 10.1016/j.jfa.2015.07.002 [12] J. S. Guo and C. H. Wu, On a free boundary for a two-species weak competition system, J. Dyn. Differential Equations, 2012, 24, 873–895. doi: 10.1007/s10884-012-9267-0 [13] J. S. Guo and C. H. Wu, Dynamics for a two-species competition-diffusion model with two free boundaries, Nonlinearity, 2015, 28, 1–27. doi: 10.1088/0951-7715/28/1/1 [14] K. P. Hadeler and M. A. Lewis, Spatial dynamics of the diffusive logistic equation with a sedentary compartment, Canad. Appl. Math. Quart., 2002, 10, 473–499. [15] Y. Kaneko and H. Matsuzawa, Spreading speed and sharp asymptotic profiles of solutions in free boundary problems for nonlinear advection-diffusion equations, J. Math. Anal. Appl., 2015, 428, 43–76. doi: 10.1016/j.jmaa.2015.02.051 [16] Y. Kaneko, H. Matsuzawa and Y. Yamada, A free boundary problem of nonlinear diffusion equation with positive bistable nonlinearity in high space dimensions Ⅰ: Classification of asymptotic behavior, Discrete Contin. Dyn. Syst., 2020, 42, 2719–2745. [17] Y. Kaneko, H. Matsuzawa and Y. Yamada, A free boundary problem of nonlinear diffusion equation with positive bistable nonlinearity in high space dimensions Ⅲ: General case, Discrete Contin. Dyn. Syst. S, 2024, 17, 742–761. doi: 10.3934/dcdss.2023089 [18] F. Li, X. Liang and W. X. Shen, Diffusive KPP equations with free boundaries in time almost periodic environments: Ⅰ. Spreading and vanishing dichotomy, Discrete Contin. Dyn. Syst., 2016, 36, 3317–3338. [19] F. Li, X. Liang and W. X. Shen, Diffusive KPP equations with free boundaries in time almost periodic environments: Ⅱ. Spreading speeds and semi-wave solutions, J. Differential Equations, 2016, 261, 2403–2445. doi: 10.1016/j.jde.2016.04.035 [20] L. Li, S. Y. Liu and M. X. Wang, A viral propagation model with a nonlinear infection rate and free boundaries, Sci. China Math., 2021, 64, 1971–1992. doi: 10.1007/s11425-020-1680-0 [21] S. Y. Liu, H. M. Huang and M. X. Wang, A free boundary problem for a prey-predator model with degenerate diffusion and predator-stage structure, Discrete Contin. Dyn. Syst. Ser. B, 2020, 25, 1649–1670. [22] S. Y. Liu and M. X. Wang, Existence and uniqueness of solution of free boundary problem with partially degenerate diffusion, Nonlinear Anal. RWA, 2020, 54, 103097. doi: 10.1016/j.nonrwa.2020.103097 [23] N. A. Maidana and H. Yang, Spatial spreading of West Nile virus described by traveling waves, J. Theoret. Biol., 2009, 258, 403–417. doi: 10.1016/j.jtbi.2008.12.032 [24] H. Monobe and C. H. Wu, On a free boundary problem for a reaction-diffusion-advection logistic model in heterogeneous environment, J. Differential Equations, 2016, 261, 6144–6177. doi: 10.1016/j.jde.2016.08.033 [25] S. Razvan and D. Gabriel, Numerical approximation of a free boundary problem for a predator-prey model, Numer. Anal. Appl., 2009, 5434, 548–555. [26] J. L. Ren, D. D. Zhu and H. Y. Wang, Spreading-vanishing dichotomy in information diffusion in online social networks with intervention, Discrete Contin. Dyn. Syst. Ser. B, 2019, 24, 1843–1865. [27] A. K. Tarboush, Z. G. Lin and M. Zhang, Spreading and vanishing in a West Nile virus model with expanding fronts, Sci. China Math., 2017, 60, 841–860. doi: 10.1007/s11425-016-0367-4 [28] C. R. Tian and S. G. Ruan, A free boundary problem for Aedes aegypti mosquito invasion, Appl. Math. Model., 2017, 46, 203–217. doi: 10.1016/j.apm.2017.01.050 [29] J. Wang and J. F. Cao, The spreading frontiers in partially degenerate reaction-diffusion systems, Nonlinear Analysis, 2015, 122, 215–238. doi: 10.1016/j.na.2015.04.003 [30] J. Wang and L. Zhang, Invasion by an inferior or superior competitor: A diffusive competition model with a free boundary in a heterogeneous environment, J. Math. Anal. Appl., 2015, 423, 377–398. doi: 10.1016/j.jmaa.2014.09.055 [31] R. Wang and Y. H. Du, Long-time dynamics of a diffusive epidemic model with free boundaries, Discrete Contin. Dyn. Syst. Ser. B, 2021, 4, 2201–2238. [32] L. Wei, C. H. Zhang and M. L. Zhou, Long time behavior for solutions of the diffusive logistic equation with advection and free boundary, Calc. Var. Partial Differ. Eq., 2016, 55, 95–128. doi: 10.1007/s00526-016-1039-y [33] S. L. Wu, Entire solutions in a bistable reaction-diffusion system modeling man-environment-man epidemics, Nonlinear Anal. RWA, 2012, 13, 1991–2005. doi: 10.1016/j.nonrwa.2011.12.020 [34] D. Xu and X. Q. Zhao, Erratum to "Bistable waves in an epidemic model", J. Dyn. Differential Equations, 2005, 17, 219–247. doi: 10.1007/s10884-005-6294-0 [35] D. W. Zhang and B. X. Dai, A free boundary problem for the diffusive intraguild predation model with intraspecific competition, J. Math. Anal. Appl., 2019, 474, 381–412. doi: 10.1016/j.jmaa.2019.01.050 [36] H. T. Zhang, L. Li and M. X. Wang, Free boundary problems for the local-nonlocal diffusive model with different moving parameters, Discrete Contin. Dyn. Syst. Ser. B, 2023, 28, 474–498. doi: 10.3934/dcdsb.2022085 [37] H. T. Zhang, L. Li and M. X. Wang, The dynamics of partially degenerate nonlocal diffusion systems with free boundaries, J. Math. Anal. Appl., 2022, 512, 126134. doi: 10.1016/j.jmaa.2022.126134 [38] K. Zhang and X. Q. Zhao, Asymptotic behavior of a reaction-diffusion model with a quiescent stage, Proc. R. Soc. Lond. A, 2007, 463, 1029–1043. [39] P. A. Zhang and W. T. Li, Monotonicity and uniqueness of traveling waves for a reaction-diffusion model with a quiescent stage, Nonlinear Anal. TMA, 2010, 72, 2178–2189. doi: 10.1016/j.na.2009.10.016 [40] W. Y. Zhang, Z. H. Liu and L. Zhou, A free boundary problem of a predator-prey model with a nonlocal reaction term, Z. Angew. Math. Phys., 2021, 72, 1–21. doi: 10.1007/s00033-020-01428-z [41] Z. D. Zhang and A. K. Tarboush, The diffusive model for West Nile virus with advection and expanding fronts in a heterogeneous environment, International Journal of Biomathematic, 2020, 13, 2050057. doi: 10.1142/S1793524520500576 [42] M. Zhao, W. T. Li and Y. Zhang, Dynamics of an epidemic model with advection and free boundaries, Math. Biosci. Eng., 2019, 16, 5991–6014. doi: 10.3934/mbe.2019300 [43] X. Q. Zhao and W. D. Wang, Fisher waves in an epidemic model, Discrete Contin. Dyn. Syst. B, 2004, 4, 1117–1128. [44] Y. Zhao and M. X. Wang, A reaction-diffusion-advection equation with mixed and free boundary conditions, J. Dyn. Differential Equations, 2018, 30, 743–777. doi: 10.1007/s10884-017-9571-9 [45] L. Zhou, S. Zhang and Z. H. Liu, A free boundary problem of a predator-prey model with advection in heterogeneous environment, Appl. Math. Comput., 2016, 289, 22–36. [46] P. Zhou and D. M. Xiao, The diffusive logistic model with a free boundary in heterogeneous environment, J. Differential Equations, 2014, 256, 1927–1954. [47] D. D. Zhu, J. L. Ren and H. P. Zhu, Spatial-temporal basic reproduction number and dynamics for a dengue disease diffusion model, Math. Method. Appl. Sci., 2018, 41, 5388–5403. -
-
-
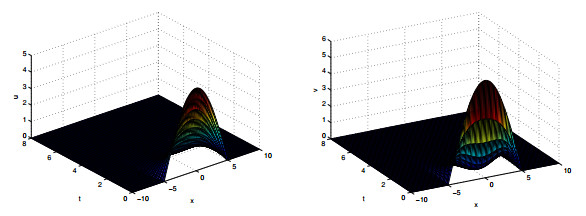
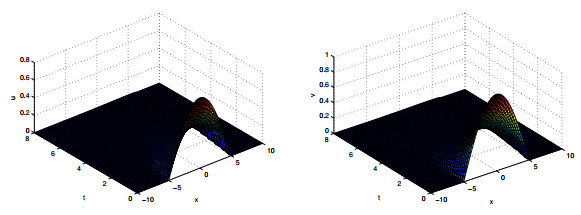
Figure 1.
$ a_{11}=2, a_{12}=a_{21}=1, a_{22}=1.2, a=0.5, b=0.8, h_{0}=5. $ -
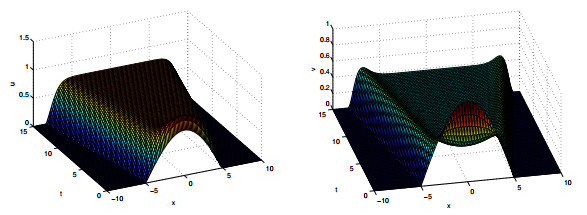
Figure 2.
$ a_{11}=2, a_{12}=a_{21}=1, a_{22}=1.2, a=5, b=6, h_{0}=5. $ -
Figure 3.
$ a_{11}=1, a_{12}=2, a_{21}=2.1, a_{22}=1, a=8, b=1, h_{0}=5. $ -
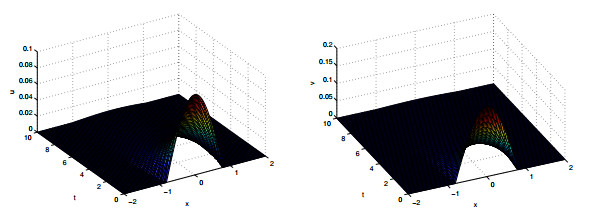
Figure 4.
$ a_{11}=1, a_{12}=2.5, a_{21}=2, a_{22}=2, a=0.1, b=0.2, h_{0}=0.8. $ -
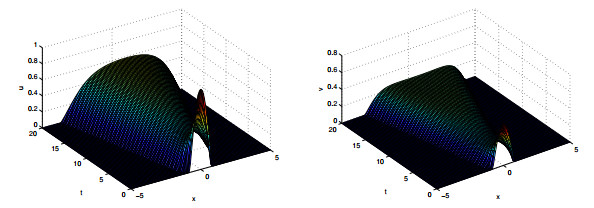
Figure 5.
$ a_{11}=1, a_{12}=2.5, a_{21}=2, a_{22}=2, a=1, b=0.5, h_{0}=0.8. $




 DownLoad:
DownLoad: