| Citation: |
Weijun He, Weiguo Rui, Xiaochun Hong. AN EXTENSIONAL CONFORMABLE FRACTIONAL DERIVATIVE AND ITS EFFECTS ON SOLUTIONS AND DYNAMICAL PROPERTIES OF FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(3): 1790-1819. doi: 10.11948/20230418
|
AN EXTENSIONAL CONFORMABLE FRACTIONAL DERIVATIVE AND ITS EFFECTS ON SOLUTIONS AND DYNAMICAL PROPERTIES OF FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS
-
Abstract
Investigations have shown that the conformable fractional derivative is very different from the classical fractional derivatives, it does not have function of memory like the classical fractional derivatives, so it is more appropriate to be called as cognate derivative of the classical integer-order derivative. In this paper, following the idea of constructing the conformable fractional derivative, an extensional conformable fractional derivative named sech-fractional derivative is proposed. The effects of the new conformable fractional differential operator on dynamical properties of nonlinear partial differential equations (PDEs) are discussed. As example, by using the dynamical system method, traveling wave solutions and their dynamical properties of a nonlinear fractional Schrödinger equation are investigated under the sech-fractional differential operator. The solutions and their dynamical properties of the nonlinear Schrödinger equation are compared under three kinds of differential operators, their distinction and connection are revealed. Some interesting phenomena are found and deserve attentions further.
-
-
References
[1] T. Abdeljawad, On conformable fractional calculus, Journal of Computational and Applied Mathematics, 2015, 279, 57–66. doi: 10.1016/j.cam.2014.10.016 [2] B. Acay, E. Bas and T. Abdeljawad, Non-local fractional calculus from different viewpoint generated by truncated M-derivative, Journal of Computational and Applied Mathematics, 2020, 366, 112410. doi: 10.1016/j.cam.2019.112410 [3] E. Balci, İ. Öztürk and S. Kartal, Dynamical behaviour of fractional order tumor model with Caputo and conformable fractional derivative, Chaos, Solitons and Fractals, 2019, 123, 43–51. doi: 10.1016/j.chaos.2019.03.032 [4] Y. Cenesiz and K. Ali, The new solution of time fractional wave equation with conformable fractional derivative definition, Journal of New Theory, 2015, 7, 79–85. [5] W. S. Chung, Fractional Newton mechanics with conformable fractional derivative, Journal of Computational and Applied Mathematics, 2015, 290, 150–158. doi: 10.1016/j.cam.2015.04.049 [6] M. T. Darvishi, M. Najafi and A. R. Seadawy, Dispersive bright, dark and singular optical soliton solutions in conformable fractional optical fiber Schrödinger models and its applications, Optical and Quantum Electronics, 2018, 50(4), 1–16. [7] M. Ekici, M. Mirzazadeh, M. Eslami, et al., Optical soliton perturbation with fractional-temporal evolution by first integral method with conformable fractional derivatives, Optik, 2016, 127(22), 10659–10669. doi: 10.1016/j.ijleo.2016.08.076 [8] A. El-Ajou, M. N. Oqielat, Z. Al-Zhour, et al, Solitary solutions for time-fractional nonlinear dispersive PDEs in the sense of conformable fractional derivative, Chaos, 2019, 29(9), 093102. doi: 10.1063/1.5100234 [9] M. Eslami and H. Rezazadeh, The first integral method for Wu-Zhang system with conformable time-fractional derivative, Calcolo, 2016, 53(3), 475–485. doi: 10.1007/s10092-015-0158-8 [10] J. H. He, S. K. Elagan and Z. B. Li, Geometrical explanation of the fractional complex trnsform and derivative chain rule for fractional calculus, Physica Letters A, 2012, 376, 257–259. doi: 10.1016/j.physleta.2011.11.030 [11] Y. He and Y. Zhao, Applications of separation variables approach in solving time-fractional PDEs, Mathematical Problems in Engineering, 2018, 2018. [12] X. Hong, A. G. Davodi, S. M. Mirhosseini-Alizamini, et al., New explicit solitons for the general modified fractional Degasperis-Procesi-Camassa-Holm equation with a truncated M-fractional derivative, Modern Physics Letters B, 2021, 35(33), 2150496. doi: 10.1142/S0217984921504960 [13] A. Hussain, A. Jhangeer, N. Abbas, et al., Optical solitons of fractional complex Ginzburg-Landau equation with conformable, beta, and M-truncated derivatives: A comparative study, Advances in Difference Equations, 2020, 2020(1), 1–19. doi: 10.1186/s13662-019-2438-0 [14] E. İhan and İ O. Kiymaz, A generalization of truncated M-fractional derivative and applications to fractional differential equations, Applied Mathematics and Nonlinear Sciences, 2020, 5(1), 171–188. doi: 10.2478/amns.2020.1.00016 [15] O. S. Iyiola and E. R. Nwaeze, Some new results on the new conformable fractional calculus with application using D'Alambert approach, Progress in Fractional Differentiation and Applications, 2016, 2(2), 115–122. doi: 10.18576/pfda/020204 [16] G. Jumarie, Modified Riemann-Liouville derivative and fractional Talor series of non-differentiable functions further results, Computers and Mathematics with Applications, 2006, 51(9–10), 1367–1376. [17] G. Jumarie, Fractional partial differential equations and modified Riemann-Liouville derivative new methods for solution, Journal of Applied Mathematics and Computing, 2007, 24(1–2), 31–48. [18] G. Jumarie, Cauchy's integral formula via the modified Riemann-Liouville derivative for analytic functions of fractional order, Applied Mathematics Letters, 2010, 23(12), 1444–1450. doi: 10.1016/j.aml.2010.08.001 [19] R. Khalil, M. Al Horani, A. Yousef, et al., A new definition of fractional derivative, Journal of Computational and Applied Mathematics, 2014, 264, 65–70. doi: 10.1016/j.cam.2014.01.002 [20] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and Applications of Fractional Differential Equations, Elsevier, 2006. [21] J. Li and Z. Liu, Smooth and non-smooth traveling waves in a nonlinearly dispersive equation, Applied Mathematical Modelling, 2000, 25(1), 41–56. doi: 10.1016/S0307-904X(00)00031-7 [22] J. Li and L. Zhang, Bifurcations of traveling wave solutions in generalized Pochhammer-Chree equation, Chaos, Solitons and Fractals, 2002, 14(4), 581–593. doi: 10.1016/S0960-0779(01)00248-X [23] X. Li, Comment on "Applications of homogenous balanced principle on investigating exact solutions to a series of time fractional nonlinear PDEs", Communications in Nonlinear Science and Numerical Simulation, 2018, 59, 606–607. doi: 10.1016/j.cnsns.2017.12.006 [24] N. G. N'Gbo and Y. Xia, Traveling wave solution of bad and good modified Boussinesq equations with conformable fractional-order derivative, Qualitative Theory of Dynamical Systems, 2022, 21(1), 1–21. doi: 10.1007/s12346-021-00531-4 [25] M. S. Osman, A. Zafar, K. K. Ali, et al., Novel optical solitons to the perturbed Gerdjikov-Ivanov equation with truncated M-fractional conformable derivative, Optik, 2020, 222, 165418. doi: 10.1016/j.ijleo.2020.165418 [26] H. Rezazadeh, S. Mirhosseini-Alizamin and R. Attia, New exact optical soliton solutions for the General Modified fractional Degasperis-Procesi-Camassa-Holm equations with a truncated M-fractional derivative, Modern Physics Letters B, 2021, 35(33), 17 pp. [27] M. B. Riaz, A. Jhangeer, J. Awrejcewicz, et al., Fractional propagation of short light pulses in monomode optical fibers: Comparison of Beta derivative and truncated M-fractional derivative, Journal of Computational and Nonlinear Dynamics, 2022, 17(3), 031002, 9 pp. [28] W. Rui, Applications of integral bifurcation method together with homogeneous balanced principle on investigating exact solutions of time fractional nonlinear PDEs, Nonlinear Dynamics, 2018, (91), 697-712. [29] W. Rui, Dynamical system method for investigating existence and dynamical property of solution of nonlinear time-fractional PDEs, Nonlinear Dynamics, 2020, 99(3), 2421–2440. doi: 10.1007/s11071-019-05410-x [30] W. Rui, Separation method of semi-fixed variables together with dynamical system method for solving nonlinear time-fractional PDEs with higher-order terms, Nonlinear Dynamics, 2022, 109, 943–961. doi: 10.1007/s11071-022-07463-x [31] S. Salahshour, A. Ahmadian, S. Abbasbandy, et al., M-fractional derivative under interval uncertainty: Theory, properties and applications, Chaos, Solitons and Fractals, 2018, 117, 84–93. doi: 10.1016/j.chaos.2018.10.002 [32] J. E. Solís-Pérez and J. F. Gómez-Aguilar, Novel fractional operators with three orders and power-law, exponential decay and Mittag-Leffler memories involving the truncated M-derivative, Symmetry, 2020, 12(4), 626. doi: 10.3390/sym12040626 [33] J. Sousa, E. C. de Oliveira, A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties, arXiv preprint, arXiv: 1704.08187, 2017. [34] T. A. Sulaiman, G. Yel and H. Bulut, M-fractional solitons and periodic wave solutions to the Hirota-Maccari system, Modern Physics Letters B, 2019, 33(05), 1950052. doi: 10.1142/S0217984919500520 [35] A. S. Tagne, J. M. Ema'a Ema'a, G. H. Ben-Bolie, et al., A new truncated M-fractional derivative for air pollutant dispersion, Indian Journal of Physics 2020, 94(11), 1777-1784. doi: 10.1007/s12648-019-01619-z [36] V. E. Tarasov, On chain rule for fractional derivatives, Communications in Nonlinear Science and Numerical Simulation, 2016, 30(1), 1–4. [37] K. U. Tariq, M. Younis, S. T. R. Rizvi, et al., M-truncated fractional optical solitons and other periodic wave structures with Schrödinger-Hirota equation, Modern Physics Letters B, 2020, 34(supp01), 2050427. doi: 10.1142/S0217984920504278 [38] U. Younas, M. Younis, A. R. Seadawy, et al., Diverse exact solutions for modified nonlinear Schrödinger equation with conformable fractional derivative, Results in Physics, 2021, 20, 103766. doi: 10.1016/j.rinp.2020.103766 [39] A. Zafar, A. Bekir, M. Raheel, et al., Optical soliton solutions to Biswas-Arshed model with truncated M-fractional derivative, Optik, 2020, 222, 165355. doi: 10.1016/j.ijleo.2020.165355 [40] B. Zhang, W. Zhu, Y. Xia, et al., A unified analysis of exact traveling wave solutions for the fractional-order and integer-order Biswas-Milovic equation: via bifurcation theory of dynamical system, Qualitative Theory of Dynamical Systems, 2020, 19(1), 1–28. doi: 10.1007/s12346-019-00337-5 [41] D. Zhao and M. Luo, General conformable fractional derivative and its physical interpretation, Calcolo, 2017, 54(3), 903–917. doi: 10.1007/s10092-017-0213-8 [42] H. Zheng, Y. Xia, Y. Bai, et al., Travelling wave solutions of the general regularized long wave equation, Qualitative Theory of Dynamical Systems, 2021, 20(1), 1–21. doi: 10.1007/s12346-020-00443-9 [43] W. Zhu, Y. Xia, B. Zhang, et al., Exact traveling wave solutions and bifurcations of the time-fractional differential equations with applications, International Journal of Bifurcation and Chaos, 2019, 29(03), 1950041. doi: 10.1142/S021812741950041X -
-
Figures(10)
Export File
Citation
Weijun He, Weiguo Rui, Xiaochun Hong. AN EXTENSIONAL CONFORMABLE FRACTIONAL DERIVATIVE AND ITS EFFECTS ON SOLUTIONS AND DYNAMICAL PROPERTIES OF FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(3): 1790-1819. doi: 10.11948/20230418
Format
Content
DownLoad:
-
Figure 1.
Graphs of the (2.35) and (2.37) under the
$ A=2, \ k=0.8, \ c=0.5, \ \alpha=0.25, \ \beta=0.75, \ t=1. $ -
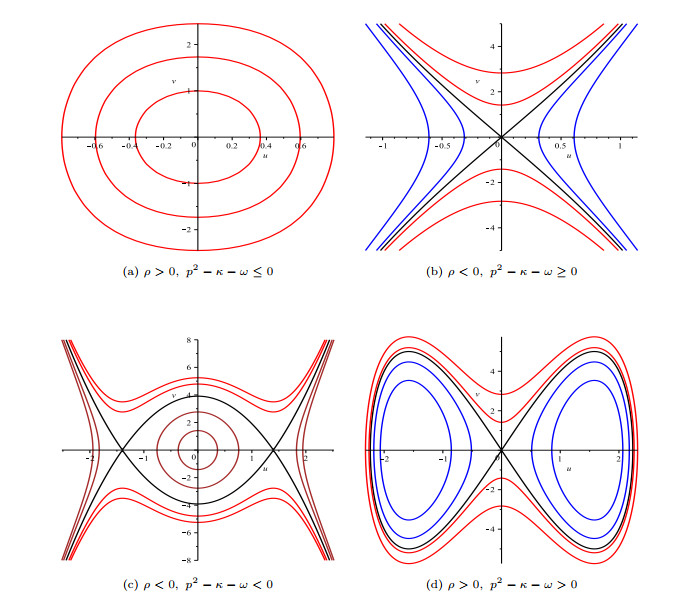
Figure 2.
Graphs of phase portraits of the system (3.10).
-
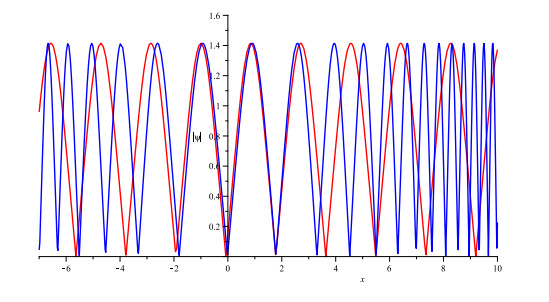
Figure 3.
Comparison graph of modules of the solutions (3.18) and (3.19).
-
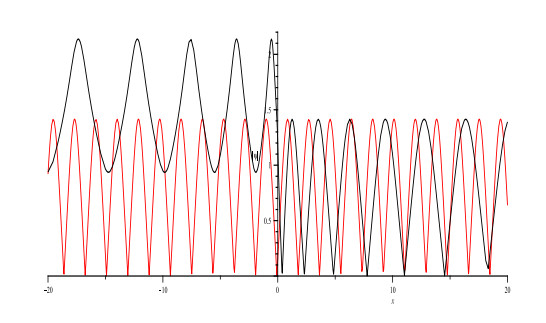
Figure 4.
Comparison graph of modules of solutions (3.20) and (3.19).
-
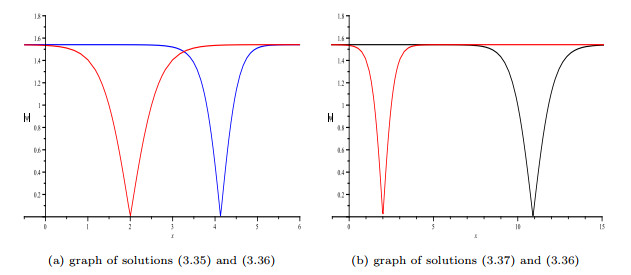
Figure 5.
Comparison graphs of modules of solutions (3.35), (3.36) and (3.37).
-
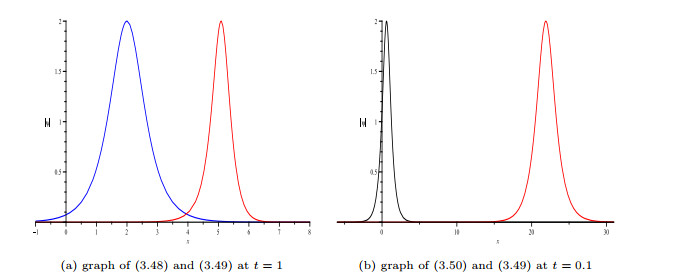
Figure 6.
Comparison graphs of modules of solutions (3.48), (3.49) and (3.50).
-
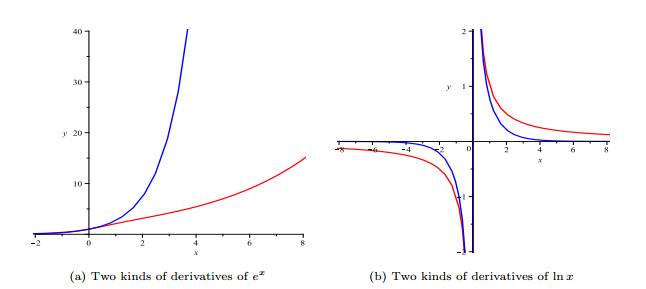
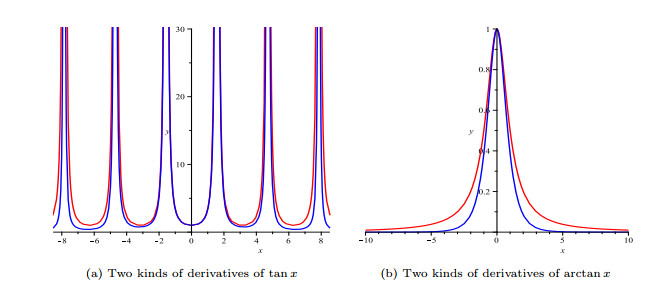
Figure 7.
Graphs of derivatives defined by (5.2) under two operators.
-
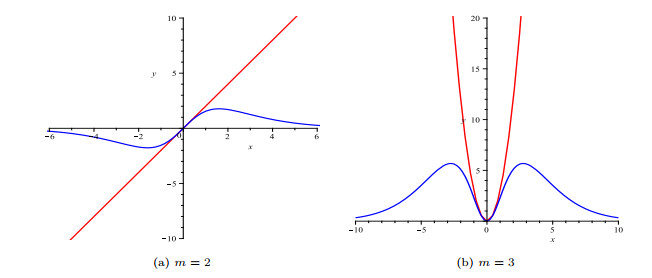
Figure 8.
Graphs of functions defined by (5.3) and (5.4) under two operators.
-
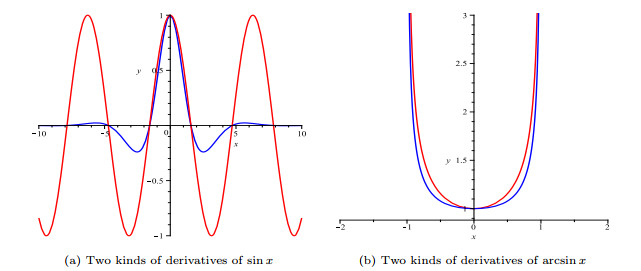
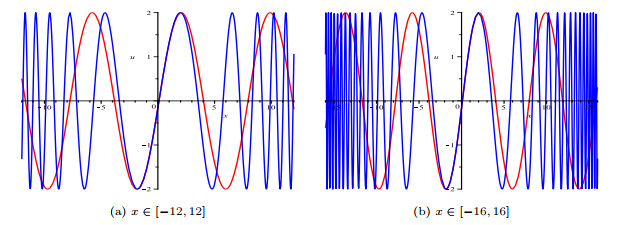
Figure 9.
Graphs of functions defined by (5.5) and (5.6) under two operators.
-
Figure 10.
Graphs of functions defined by (5.7) and (5.8) under two operators.