| Citation: |
S. Kumbinarasaiah, Hadi Rezazadeh, Hijaz Ahmad. A NOVEL APPROACH FOR THE NONLINEAR ELLIPTIC PARTIAL DIFFERENTIAL EQUATIONS USING CLIQUE POLYNOMIALS OF GRAPH[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 56-75. doi: 10.11948/20230419
|
A NOVEL APPROACH FOR THE NONLINEAR ELLIPTIC PARTIAL DIFFERENTIAL EQUATIONS USING CLIQUE POLYNOMIALS OF GRAPH
-
Abstract
This study proposed an efficient numerical technique for nonlinear elliptic partial differential equations (EPDEs) using the functional matrix generated by Clique polynomials of Complete Graph. Recently, Graph theory has attracted many mathematicians' attention due to its wide applications. Here, Three nonlinear problems have been considered to examine the proposed scheme proficiency. Some theorems on convergence are discussed. Here, the nonlinear elliptic PDEs are rehabilitated into a nonlinear algebraic equation system using the operational matrix of Clique polynomials and collocation technique. Using the Newton-Raphson method, we numerically solved this system of algebraic equations to the desired results. The proposed scheme results are compared with the literature's analytical and other method solutions through tables and graphs. Tables and graphs are used to support the proposed technique's efficacy and accuracy. The obtained results reveal that the current approach is more accurate than other methods. The theorems are used to draw the convergent analysis for the suggested approach. From the obtained results, we can conclude that to find a numerical solution for these kinds of nonlinear EPDEs, the method is extremely effective, requires less computational effort, and is easy to implement.
-
-
References
[1] E. F. Anley, Numerical solutions of elliptic partial differential equations by using finite volume method, Pure and Applied Mathematics Journal, 2016, 5(4), 120–129. doi: 10.11648/j.pamj.20160504.16 [2] C. S. Chen, C. M. Fan and P. H. Wen, The method of approximate particular solutions for solving elliptic problems with variable coefficients, International Journal of Computational Methods, 2011, 8(3), 545–559. doi: 10.1142/S0219876211002484 [3] C. Conca and S. Natesan, Numerical methods for elliptic partial differential equations with rapidly oscillating coefficients, Comput. Methods Appl. Mech. Engrg., 2003, 192, 47–76. doi: 10.1016/S0045-7825(02)00500-5 [4] P. Concus, G. H. Golub and D. P. O'Leary, Numerical solution of nonlinear elliptic partial differential equations by a generalized conjugate gradient method, Computing, 1978, 19, 321–339. doi: 10.1007/BF02252030 [5] Z. Eidinejad, R. Saadati, J. Vahidi and C. Li, Numerical solutions of 2D stochastic time‐fractional Sine–Gordon equation in the Caputo sense, International Journal of Numerical Modelling: Electronic Networks, Devices and Fields, 2023, 36(6), e3121. doi: 10.1002/jnm.3121 [6] R. M. Ganji, H. Jafari, M. Kgarose and A. Mohammadi, Numerical solutions of time-fractional Klein-Gordon equations by clique polynomials, Alexandria Engineering Journal, 2021, 60(5), 4563–4571. doi: 10.1016/j.aej.2021.03.026 [7] L. Gavete, F. Ureña, J. J. Benito, A. García, M. Ureña and E. Salete, Solving second-order non-linear elliptic partial differential equations using generalized finite difference method, Journal of Computational and Applied Mathematics, 2017, 318, 378–387. doi: 10.1016/j.cam.2016.07.025 [8] B. K. Ghimire, H. Y. Tian and A. R. Lamichhane, Numerical solutions of elliptic partial differential equations using Chebyshev polynomials, Computers and Mathematics with Applications, 2016, 72, 1042–1054. doi: 10.1016/j.camwa.2016.06.012 [9] Z. Hainan, G. Jianhou and G. Wei, Fuzzy fractional factors in fuzzy graphs-Ⅱ, International Journal of Mathematics and Computer in Engineering, 2024, 2(2), 155–164. doi: 10.2478/ijmce-2024-0012 [10] J. G. Hoskins, V. Rokhlin and K. Serkh, On the numerical solution of elliptic partial differential equations on polygonal domains, Siam J. Sci. Comput., 2019, 41(4), a2552–a2578. doi: 10.1137/18M1199034 [11] M. Izadi, J. Singh and S. Noeiaghdam, Simulating accurate and effective solutions of some nonlinear nonlocal two-point BVPs: Clique and QLM-clique matrix methods, Heliyon, 2023, 9(11), e22267. doi: 10.1016/j.heliyon.2023.e22267 [12] M. Izadi and H. M. Srivastava, Fractional clique collocation technique for numerical simulations of fractional-order Brusselator chemical model, Axioms, 2022, 11(11), 654. doi: 10.3390/axioms11110654 [13] L. Juanjuan, Z. Linli and G. Wei, Remarks on bipolar cubic fuzzy graphs and its chemical applications, International Journal of Mathematics and Computer in Engineering, 2023, 1(1), 1–10. doi: 10.2478/ijmce-2023-0001 [14] S. Kumbinarasaiah, Numerical solution for the (2+1) dimensional Sobolev and regularized long wave equations arise in fluid mechanics via wavelet technique, Partial Differential Equations in Applied Mathematics, 2021, 3, 100016. DOI: 10.1016/j.padiff.2020.100016. [15] S. Kumbinarasaiah, A new approach for the numerical solution for nonlinear Klein–Gordon equation, SeMA, 2020, 77, 435–436. doi: 10.1007/s40324-020-00225-y [16] S. Kumbinarasaiah and G. Manohara, A novel approach for the system of coupled differential equations using clique polynomials of graph, Partial Differential Equations in Applied Mathematics, 2022, 5, 100181. doi: 10.1016/j.padiff.2021.100181 [17] S. Kumbinarasaiah and M. Mulimani, Comparative study of Adomian decomposition method and clique polynomial method, Partial Differential Equations in Applied Mathematics, 2022, 6, 100454. doi: 10.1016/j.padiff.2022.100454 [18] S. Kumbinarasaiah and R. A. Mundewadi, The new operational matrix of integration for the numerical solution of integrodifferential equations via Hermite wavelet, SeMA, 2021, 78, 367–384. doi: 10.1007/s40324-020-00237-8 [19] S. Kumbinarasaiah and M. P. Preetham, A study on homotopy analysis method and clique polynomial method, Computational Methods for Differential Equations, 2022, 10(3), 774–788. [20] S. Kumbinarasaiah and K. R. Raghunatha, Study of special types of boundary layer natural convection flow problems through the clique polynomial method, Heat Transfer, 2022, 51(1), 434–450. doi: 10.1002/htj.22314 [21] S. H. Lui, On monotone and Schwarz alternating methods for nonlinear elliptic PDEs, ESAIM: Mathematical Modelling and Numerical Analysis, 2001, 35(1), 1–15. doi: 10.1051/m2an:2001104 [22] S. H. Lui, On linear monotone iteration and Schwarz methods for nonlinear elliptic PDEs, Numerische Mathematik, 2002, 93, 109–129. [23] M. Mallanagoud and S. Kumbinarasaiah, A new approach to the Benjamin-Bona-Mahony equation via ultraspherical wavelets collocation method, International Journal of Mathematics and Computer in Engineering, 2024, 2(2), 179–192. doi: 10.2478/ijmce-2024-0014 [24] N. Muhammad, J. Shamoona, A. Farkhanda and Z. Aqib, Solving the generalized equal width wave equation via sextic B-spline collocation technique, International Journal of Mathematics and Computer in Engineering, 2023, 1(2), 229–242. doi: 10.2478/ijmce-2023-0019 [25] P. K. Pandey and S. S. A. Jaboob, A finite difference method for a numerical solution of elliptic boundary value problems, Applied Mathematics and Nonlinear Sciences, 2018, 3(1), 311–320. doi: 10.21042/AMNS.2018.1.00024 [26] H. S. Ramane, et al., Numerical solution for nonlinear Klein Gordon equation via Operational-Matrix by clique polynomial of complete graphs, Int. J. Appl. Comput. Math., 2021, 12. [27] S. C. Shiralashetti, M. H. Kantli and A. B. Deshi, New wavelet-based full-approximation scheme for the numerical solution of nonlinear elliptic partial differential equations, Alexandria Engineering Journal, 2016, 55(3), 2797–2804. doi: 10.1016/j.aej.2016.07.019 [28] S. C. Shiralashetti and S. Kumbinarasaiah, Theoretical study on continuous polynomial wavelet bases through wavelet series collocation method for nonlinear lane-Emden type equations, Applied Mathematics and Computation, 2017, 315, 591–602. doi: 10.1016/j.amc.2017.07.071 [29] S. C. Shiralashetti and S. Kumbinarasaiah, Laguerre wavelets collocation method for the numerical solution of the Benjamina Bona Mohany equations, Journal of Taibah University for Science, 2019, 13(1), 9–15. DOI: 10.1080/16583655.2018.1515324. [30] S. C. Shiralashetti and S. Kumbinarasaiah, CAS wavelets analytic solution and Genocchi polynomials numerical solutions for the integral and integrodifferential equations, Journal of Interdisciplinary Mathematics, 2019, 22(3), 201–218. doi: 10.1080/09720502.2019.1602354 [31] S. C. Shiralashetti, and S. Kumbinarasaiah, Hermite wavelets operational matrix of integration for the numerical solution of nonlinear singular initial value problems, Alexandria Engineering Journal, 2018, 57(4), 2591–2600. doi: 10.1016/j.aej.2017.07.014 [32] K. Srinivasa and H. Rezazadeh, Numerical solution for the fractional-order one-dimensional telegraph equation via wavelet technique, Int. J. Nonlinear Sci. Numer. Simulation, 2021, 22(6), 767–780. doi: 10.1515/ijnsns-2019-0300 [33] K. Srinivasa, H. Rezazadeh and W. Adel, Numerical investigation based on Laguerre wavelet for solving the hunter Saxton equation, Int. J. Appl. Comput. Math., 2020, 6, 139. doi: 10.1007/s40819-020-00890-7 [34] S. Yuzbasi and M. E. Tamar, A new approaching method for linear neutral delay differential equations by using clique polynomials, Turkish Journal of Mathematics, 2023, 47(7), 2098–2121. doi: 10.55730/1300-0098.3483 -
-
Figures(7) / Tables(2)
Export File
Citation
S. Kumbinarasaiah, Hadi Rezazadeh, Hijaz Ahmad. A NOVEL APPROACH FOR THE NONLINEAR ELLIPTIC PARTIAL DIFFERENTIAL EQUATIONS USING CLIQUE POLYNOMIALS OF GRAPH[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 56-75. doi: 10.11948/20230419
Format
Content
DownLoad:
-
Figure 1.
Complete graph with 4 vertices
$ K_{4} $ -
Figure 2.
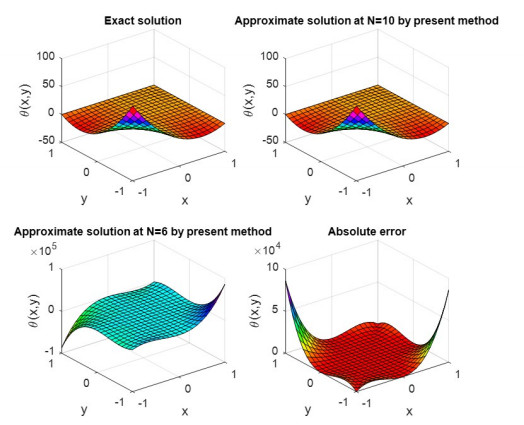
Assessment of Clique polynomial method with the exact solution for the example 1.
-
Figure 3.
Comparison of Clique polynomial method with the exact solution for the example 1 at distinct values of
$ y $ -
Figure 4.
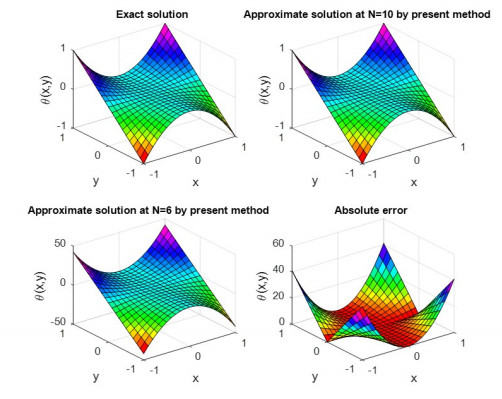
Assessment of Clique polynomial method with the exact solution for the example 2.
-
Figure 5.
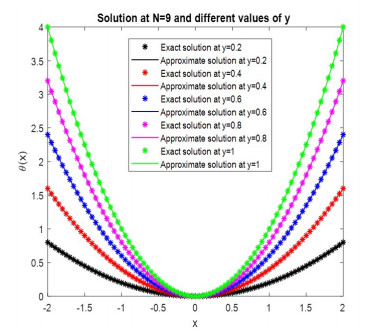
Assessment of Clique polynomial method with the exact solution, for example 2 at different values of
$ y $ -
Figure 6.
Assessment of Clique polynomial method with the exact solution for example 2 at different values of
$ x $ -
Figure 7.
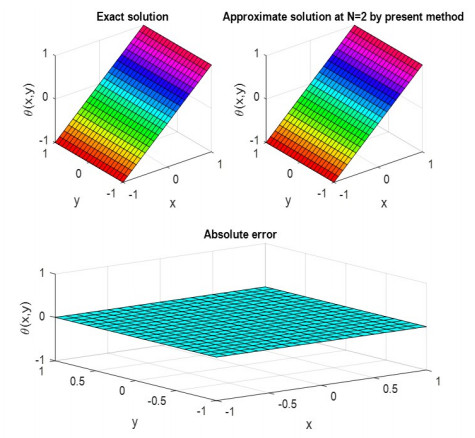
Assessment of Clique polynomial method with the exact solution for the example 3.