| Citation: | Qun Bin, Wentao Huang, Jing Li, Shi Liang. TRAVELING FRONTS OF A REAL SUPERCRITICAL QUINTIC GINZBURG-LANDAU EQUATION COUPLED BY A SLOW DIFFUSION MODE[J]. Journal of Applied Analysis & Computation, 2024, 14(5): 2862-2876. doi: 10.11948/20230457 |
TRAVELING FRONTS OF A REAL SUPERCRITICAL QUINTIC GINZBURG-LANDAU EQUATION COUPLED BY A SLOW DIFFUSION MODE
-
Abstract
In this paper, we investigate the existence of traveling front solutions for a class of quintic Ginzburg-Landau equations coupled with a slow diffusion mode. By employing the theory of geometric singular perturbations, we turn the problem into a geometric perturbation problem. We demonstrate the intersection property of the critical manifold and further validate the existence of heteroclinic orbits by computing the zeros of the Melnikov function on the critical manifold. The results demonstrate that under certain parameters, there is 1 or 2 heteroclinic solutions, confirming the existence of traveling front solutions for the considered quintic Ginzburg-Landau equation coupled with a slow diffusion mode.
-

-
References
[1] S. Behera and A. Khare, Classical $\phi^6$-field theory in (1 + 1) dimensions. A model for structural phase transitions, Pramana, 1980, 15, 245–269. doi: 10.1007/BF02847222 CrossRef $\phi^6$-field theory in (1 + 1) dimensions. A model for structural phase transitions" target="_blank">Google Scholar
[2] M. Cross and P. Hohenberg, Pattern formation outside of equilibrium, Rev. Modern Phys., 1993, 65, 851–1112. doi: 10.1103/RevModPhys.65.851 [3] R. DiPrima, W. Eckhaus and L. Segel, Non-linear wave-number interaction in near-critical two-dimensional flows, J. Fluid Mech., 1971, 49, 705–744. doi: 10.1017/S0022112071002337 [4] A. Doelman, R. Gardner and T. Kaper, Large stable pulse solutions in reaction-diffusion equations, Indiana Univ. Math. J., 2001, 50, 443–507. doi: 10.1512/iumj.2001.50.1873 [5] A. Doelman, G. Hek and N. Valkhoff, Algebraically decaying pulses in a Ginzburg-Landau system with a neutrally stable mode, Nonlinearity, 2007, 20, 357–389. doi: 10.1088/0951-7715/20/2/007 [6] A. Doelman, G. Hek and N, Valkhoff, Stabilization by slow diffusion in a real Ginzburg-Landau system, J. Nonlinear Sci., 2004, 14, 237–278. doi: 10.1007/BF02666022 [7] N. Fenichel, Geometric singular perturbation theory for ordinary differential equations, J. Differential Equations, 1979, 31, 53–98. doi: 10.1016/0022-0396(79)90152-9 [8] V. Ginzburg and L. Landau, On the theory of superconductivity, Zh. Eksp. Teor. Fiz., 1950, 1064–1082. [9] P. Hohenberg and A. Krekhov, An introduction to the Ginzburg-Landau theory of phase transitions and nonequilibrium patterns, Phys. Rep., 2015, 572, 1–42. doi: 10.1016/j.physrep.2015.01.001 [10] T. Kaper, Systems theory for singular perturbation problems. Analyzing multiscale phe- nomena using singular perturbation methods. American Mathematical Society short course, January 1998, 56, Baltimore, Maryland, 1999, 85. [11] E. Kengne, W. Liu, L. English and B. Malomed, Ginzburg-Landau models of nonlinear electric transmission networks, Phys. Rep., 2022, 982, 1–124. doi: 10.1016/j.physrep.2022.07.004 [12] Y. Kuramoto, Chemical Oscillations, Wave And Turbulence, Springer, New York, 1984. [13] L. Landau, On the theory of phase transitions, in collected papers of L. D. Landau, D. ter Haar ed, Pergamon, 1965, 193–216. [14] P. Marcq, H. Chaté and R. Conte, Exact solutions of the one-dimensional quintic complex Ginzburg-Landau equation, Phys. D, 1994, 73, 305–317. doi: 10.1016/0167-2789(94)90102-3 [15] S. Naghshband and M. Araghi, Solving generalized quintic complex Ginzburg-Landau equation by homotopy analysis method, Ain Shams Eng. J., 2016, 9, 607–613. [16] A. Newell, T. Passot and J. Lega, Order parameter equations for patterns, Annu. Rev. Fluid Mech., 1993, 25, 399–453. doi: 10.1146/annurev.fl.25.010193.002151 [17] A. Newell and J. Whitehead, Finite bandwidth, finite amplitude convection, J. Fluid Mech., 1969, 38, 279–303. doi: 10.1017/S0022112069000176 [18] A. Newell and J. Whitehead, Review of the finite bandwidthconcept, in proceedings of the international union of theoretical and applied mechanics, symposium on instability of continuous systems (1969), H. Leipholz ed, Springer-Verlag, Berlin, 1971, 279–303. [19] P. Pieribyline and G. Strinatibyline, Strong-coupling limit in the evolution from BCS superconductivity to Bose-Einstein condensation, Phys. Rev. B., 2000, 61, 15370–15381. doi: 10.1103/PhysRevB.61.15370 [20] C. Robinson, Sustained resonance for a nonlinear system with slowly varying coefficients, SIAM J. Math. Anal., 1983, 14, 847–860. doi: 10.1137/0514066 [21] B. Rosenstein and D. Li, Ginzburg-Landau theory of type Ⅱ superconductors in magnetic field, Rev. Modern Phys., 2010, 82, 109–168. doi: 10.1103/RevModPhys.82.109 [22] T. Rossides, D. Lloyd, S. Zelik and M. Turner, The dynamics of interacting multi-pulses in the one-dimensional quintic complex Ginzburg-Landau equation, SIAM J. Appl. Dyn. Syst., 2023, 22, 2242–2281. doi: 10.1137/22M1519195 [23] L. Segel, Distant side-walls cause slow amplitude modulation of cellular convection, J. Fluid Mech., 1969, 38, 203–224. doi: 10.1017/S0022112069000127 [24] L. Sieberer, M. Buchhold and S. Diehl, Keldysh field theory for driven open quantum systems, Rep. Progr. Phys., 2016, 79, 096001. doi: 10.1088/0034-4885/79/9/096001 [25] J. Soto-Crespo, N. Akhmediev and V. Afanasjev, Stability of the pulselike solutions of the quintic complex Ginzburg-Landau equation, J. Opt. Soc. Amer. B Opt. Phys., 1996, 13, 1439–1449. doi: 10.1364/JOSAB.13.001439 [26] K. Stewartson and J. Stuart, A nonlinear instability theory for a wave system in plane poiseuille flow, J. Fluid Mech., 1971, 48, 529–545. doi: 10.1017/S0022112071001733 [27] M. Tu, J. Shen and Z. Zhou, Traveling fronts of a real supercritical Ginzburg-Landau equation coupled by a slow diffusion, Qual. Theory Dyn. Syst., 2018, 17, 29–48. doi: 10.1007/s12346-017-0264-x [28] S. Yao, E. IIhan, P. Veeresha and H. Baskonus, A powerful iterative approach for quintic complex Ginzburg-Landau equation within the frame of fractional operator, Fractals, 2021, 29, 1. -
-
-
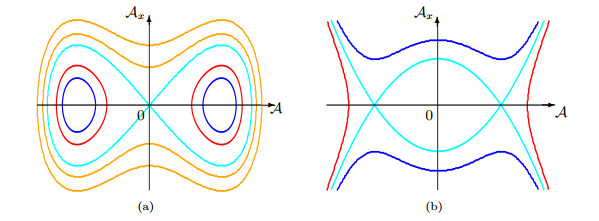
Figure 1.
(a) Global phase portraits of the one-dimensional subcritical RGLE, (b) Global phase portraits of the one-dimensional supercritical RGLE.
-
Figure 2.
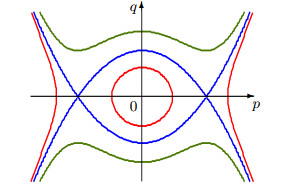
The plane portrait of the Hamiltonian system (2.5).
-
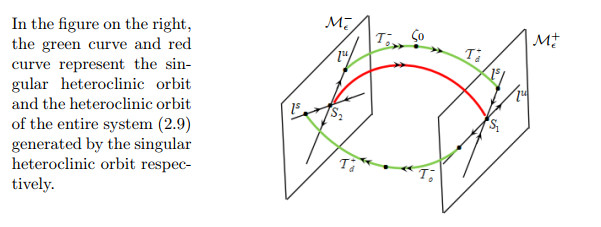
Figure 3.
Schematic diagram of heteroclinic solutions for the system-wide (2.9).




 DownLoad:
DownLoad: