| Citation: |
Litao Zhang, Xiaojing Zhang, Jianfeng Zhao. A PARAMETERIZED SHIFT-SPLITTING PRECONDITIONER FOR SADDLE POINT PROBLEMS[J]. Journal of Applied Analysis & Computation, 2024, 14(5): 2877-2889. doi: 10.11948/20230463
|
A PARAMETERIZED SHIFT-SPLITTING PRECONDITIONER FOR SADDLE POINT PROBLEMS
-
Abstract
Recently, Chen and Ma [Journal of Computational and Applied Mathematics, 344(2018): 691–700] constructed the generalized shift-splitting (GSS) preconditioner, and gave the corresponding theoretical analysis and numerical experiments. In this paper, based on the generalized shift-splitting (GSS) preconditioner, we generalize their algorithms and further study the parameter shift-splitting (PSS) preconditioner for complex symmetric linear systems. Moreover, by similar theoretical analysis, we obtain that the parameter shift-splitting iterative method is unconditionally convergent. In finally, one example is provided to confirm the effectiveness.
-
-
References
[1] M. S. Alkousa, A. V. Gasnikov, D. M. Dvinskikh, D. A. Kovalev and F. S. Stonyakin, Accelerated methods for Saddle-Point problem, Computational Mathematics and Mathematical Physics, 2020, 60(11), 1787–1809. doi: 10.1134/S0965542520110020 [2] O. Axelsson and A. Kucherov, Real valued iterative methods for solving complex symmetric linear systems, Numerical Linear Algebra with Applications, 2000, 7(4), 197–218. doi: 10.1002/1099-1506(200005)7:4<197::AID-NLA194>3.0.CO;2-S [3] Z. -Z. Bai, On semi-convergence of Hermitian and skew-Hermitian splitting methods for singular linear systems, Computing, 2010, 89(3–4), 171–197. [4] Z. -Z. Bai, On Hermitian and skew-Hermitian splitting iteration methods for continuous Sylvester equations, Journal of Computational Mathematics, 2011, 29(2), 185–198. doi: 10.4208/jcm.1009-m3152 [5] Z. Z. Bai, Optimal parameters in the HSS-like methods for saddle-point problems, Numerical Linear Algebra with Applications, 2009, 16(6), 447–479. doi: 10.1002/nla.626 [6] Z. -Z. Bai, M. Benzi and F. Chen, On preconditioned MHSS iteration methods for complex symmetric linear systems, Numerical Algorithms, 2011, 56(2), 297–317. doi: 10.1007/s11075-010-9441-6 [7] Z. -Z. Bai, M. Benzi and F, Chen, Modified HSS iteration methods for a class of complex symmetric linear systems, Computing, 2010, 87(3–4), 93–111. [8] Z. -Z. Bai, M. Benzi, F. Chen and Z. -Q. Wang, Preconditioned MHSS iteration methods for a class of block two-by-two linear systems with applications to distributed control problems, IMA Journal of Numerical Analysis, 2013, 33(1), 343–369. doi: 10.1093/imanum/drs001 [9] Z. -Z. Bai, G. -H. Golub, L. -Z. Lu and J. -F. Yin, Block triangular and skew-Hermitian splitting methods for positive-definite linear systems, SIAM Journal on Scientific Computing, 2005, 26(3), 844–863. doi: 10.1137/S1064827503428114 [10] Z. -Z. Bai, G. -H. Golub and M. K. Ng, Hermitian and skew-Hermitian splitting methods for non-Hermitian positive definite linear systems, SIAM Journal on Matrix Analysis and Applications, 2003, 24, 603–626. doi: 10.1137/S0895479801395458 [11] Z. -Z. Bai, G. -H. Golub and M. K. Ng, On inexact Hermitian and skew-Hermitian splitting methods for non-Hermitian positive definite linear systems, Linear Algebra and its Applications, 2008, 428, 413–440. doi: 10.1016/j.laa.2007.02.018 [12] Z. -Z. Bai, G. -H. Golub and M. K. Ng, On successive-overrelaxation acceleration of the Hermitian and skew-Hermitian splitting iterations, Numerical Linear Algebra with Applications, 2007, 14(4), 319–335. doi: 10.1002/nla.517 [13] Z. -Z. Bai, G. -H. Golub and J. -Y. Pan, Preconditioned Hermitian and skew-Hermitian splitting methods for non-Hermitian positive semidefinite linear systems, Numerische Mathematik, 2004, 98(1), 1–32. doi: 10.1007/s00211-004-0521-1 [14] Z. -Z. Bai and X. -P. Guo, On Newton-HSS methods for systems of nonlinear equations with positive-definite Jacobian matrices, Journal of Computational Mathematics, 2010, 28(2), 235–260. doi: 10.4208/jcm.2009.10-m2836 [15] Z. -Z. Bai and X. Yang, On HSS-based iteration methods for weakly nonlinear systems, Applied Numerical Mathematics, 2009, 59(12), 2923–2936. doi: 10.1016/j.apnum.2009.06.005 [16] M. Benzi, A generalization of the Hermitian and skew-Hermitian splitting iteration, SIAM Journal on Matrix Analysis and Applications, 2009, 31(2), 360–374. doi: 10.1137/080723181 [17] M. Benzi and D. Bertaccini, Block preconditioning of real-valued iterative algorithms for complex linear systems, IMA Journal of Numerical Analysis, 2008, 28, 598–618. [18] M. Benzi and D. Bertaccini, Block preconditioning of real-valued iterative algorithms for complex linear systems, IMA Journal of Numerical Analysis, 2008, 28(3), 598–618. [19] M. Benzi, G. -H. Golub and J. Liesen, Numerical solution of saddle point problems, Acta Numerica, 2005, 14, 1–137. doi: 10.1017/S0962492904000212 [20] M. Bolten, M. Donatelli, P. Ferrari and I. Furci, Symbol based convergence analysis in multigrid methods for saddle point problems, Linear Algebra and its Applications, 2023, 671, 67–108. doi: 10.1016/j.laa.2023.04.016 [21] Y. Cao, J. Du and Q. Niu, Shift-splitting preconditioners for saddle point problems, Journal of Computational and Applied Mathematics, 2014, 272, 239–250. doi: 10.1016/j.cam.2014.05.017 [22] Y. Cao and Z. -R. Ren, Two variants of the PMHSS iteration method for a class of complex symmetric indefinite linear systems, Applied Mathematics and Computation, 2015, 264, 61–71. doi: 10.1016/j.amc.2015.04.049 [23] C. -R. Chen and C. -F. Ma, A generalized shift-splitting preconditioner for complex symmetric linear systems, Journal of Computational and Applied Mathematics, 2018, 344, 691–700. doi: 10.1016/j.cam.2018.06.013 [24] C. -R. Chen and C. -F. Ma, A generalized shift-splitting preconditioner for saddle point problems, Applied Mathematics Letters, 43, 2015, 49–55. doi: 10.1016/j.aml.2014.12.001 [25] D. Day and M. A. Heroux, Solving complex-valued linear systems via equivalent real formulations, SIAM Journal on Scientific Computing, 2001, 23(2), 480–498. doi: 10.1137/S1064827500372262 [26] G. Karaduman, M. Yang and R. -C. Li, A least squares approach for saddle point problems, Japan Journal of Industrial and Applied Mathematics, 2023, 40(1), 95–107. doi: 10.1007/s13160-022-00509-y [27] C. -L. Li and C. -F. Ma, On Euler preconditioned SHSS iterative method for a class of complex symmetric linear systems, ESAIM: Mathematical Modelling and Numerical Analysis, 2019, 53, 1607–1627. doi: 10.1051/m2an/2019029 [28] C. -L. Li and C. -F. Ma, On semi-convergence of parameterized SHSS method for a class of singular complex symmetric linear systems, Computers and Mathematics with Applications, 77(2), 2019, 466–475. doi: 10.1016/j.camwa.2018.09.050 [29] C. -L. Li and C. -F. Ma, Efficient parameterized rotated shift-splitting preconditioner for a class of complex symmetric linear systems, Numerical Algorithms, 2019, 80(2), 337–352. doi: 10.1007/s11075-018-0487-1 [30] C. -L. Li and C. -F. Ma, On Euler-extrapolated Hermitian/skew-Hermitian splitting method for complex symmetric linear systems, Applied Mathematics Letters, 2018, 86, 42–48. doi: 10.1016/j.aml.2018.06.016 [31] J. Li, A modified new matrix splitting preconditioner for double saddle point problems, Japan Journal of Industrial and Applied Mathematics, 2024, 41(1), 85–103. doi: 10.1007/s13160-023-00581-y [32] L. Li, T. -Z. Huang and X. -P. Liu, Modified Hermitian and skew-Hermitian splitting methods for non- Hermitian positive-definite linear systems, Numerical Linear Algebra with Applications, 2007, 14(3), 217–235. doi: 10.1002/nla.528 [33] X. Li, A. -L. Yang and Y. -J. Wu, Lopsided PMHSS iteration method for a class of complex symmetric linear systems, Numerical Algorithms, 2014, 66(3), 555–568. doi: 10.1007/s11075-013-9748-1 [34] M. Masoudi and D. K. Salkuyeh, Semiconvergence of the extended PSS method for singular generalized saddle point problems, International Journal of Computer Mathematics, 2022, 99(4), 837–851. doi: 10.1080/00207160.2021.1938010 [35] Y. Saad, Iterative Methods for Sparse Linear Systems, 2nd edn, SIAM, Philadelphia, 2003. [36] D. K. Salkuyeh, D. Hezari and V. Edalatpour, Generalized successive overrelaxation iterative method for a class of complex symmetric linear system of equations, International Journal of Computer Mathematics, 2015, 92(4), 802–815. doi: 10.1080/00207160.2014.912753 [37] D. K. Salkuyeh, M. Masoudi and D. Hezari, On the generalized shift-splitting preconditioner for saddle point problems, Applied Mathematics Letters, 2015, 48, 55–61. doi: 10.1016/j.aml.2015.02.026 [38] X. -H. Shao and H. -N. Meng, A new generalized variant of the deteriorated PSS preconditioner for nonsymmetric saddle point problems, Computers and Mathematics with Applications: An International Journal, 2023, 671, 67–108. [39] S. -L. Wu, Several variants of the Hermitian and skew-Hermitian splitting method for a class of complex symmetric linear systems, Numerical Linear Algebra with Applications, 2015, 22(2), 338–356. doi: 10.1002/nla.1952 [40] A. -L. Yang, J. An and Y. -J. Wu, A generalized preconditioned HSS method for non-Hermitian positive definite linear systems, Applied Mathematics and Computation, 2010, 216(6), 1715–1722. doi: 10.1016/j.amc.2009.12.032 [41] M. -L. Zeng and C. -F. Ma, A parameterized SHSS iteration method for a class of complex symmetric system of linear equations, Computers and Mathematics with Applications, 2016, 71(10), 2124–2131. doi: 10.1016/j.camwa.2016.04.002 [42] Q. -Q. Zheng and C. -F. Ma, A class of accelerated parameterized inexact Uzawa algorithms for complex symmetric linear systems, Applied Mathematics and Computation, 2018, 320, 547–556. doi: 10.1016/j.amc.2017.10.007 [43] Q. -Q. Zheng and C. -F. Ma, Accelerated PMHSS iteration methods for complex symmetric linear systems, Numerical Algorithms, 2016, 73(2), 501–516. doi: 10.1007/s11075-016-0105-z -
-
Figures(4) / Tables(2)
Export File
Citation
Litao Zhang, Xiaojing Zhang, Jianfeng Zhao. A PARAMETERIZED SHIFT-SPLITTING PRECONDITIONER FOR SADDLE POINT PROBLEMS[J]. Journal of Applied Analysis & Computation, 2024, 14(5): 2877-2889. doi: 10.11948/20230463
Format
Content
DownLoad:
-
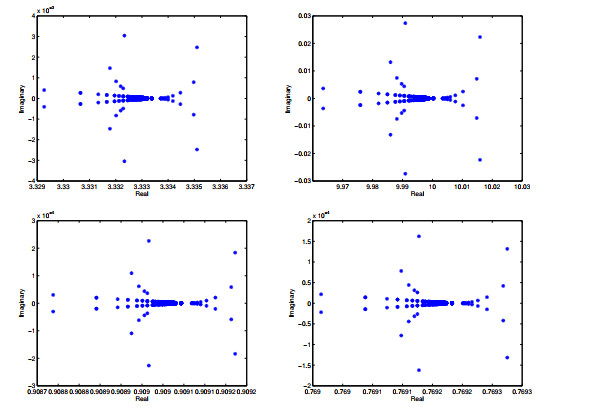
Figure 1.
The eigenvalue distribution for the generalized shift-splitting preconditioned matrix
$ \mathcal{T}_{GSS}^{-1}\mathcal {A} $ $ \alpha=\beta=0.001 $ $ \mathcal{T}_{PSS}^{-1}\mathcal {A} $ $ \alpha=\beta=0.001, \xi=0.8 $ $ \alpha=\beta=0.001, \xi=0.7 $ $ \alpha=\beta=0.001, \xi=0.5 $ $ l=16. $ -
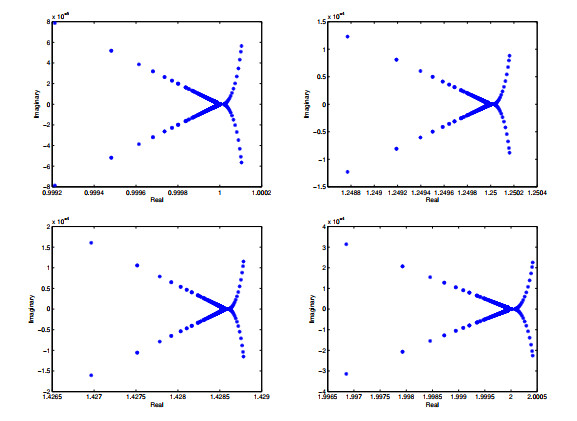
Figure 2.
The eigenvalue distribution for the parameter shift-splitting preconditioned matrix
$ \mathcal{T}_{PSS}^{-1}\mathcal {A} $ $ \alpha=\beta=0.001, \xi=0.5 $ $ \alpha=\beta=0.001, \xi=0.3 $ $ \alpha=\beta=0.001, \xi=0.1 $ $ \alpha=\beta=0.001, \xi=1.3 $ $ l=16. $ -
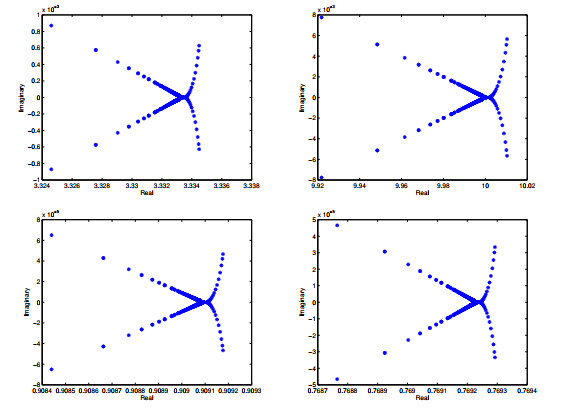
Figure 3.
The eigenvalue distribution for the generalized shift-splitting preconditioned matrix
$ \mathcal{T}_{GSS}^{-1}\mathcal {A} $ $ \alpha=\beta=0.001 $ $ \mathcal{T}_{PSS}^{-1}\mathcal {A} $ $ \alpha=\beta=0.001, \xi=0.8 $ $ \alpha=\beta=0.001, \xi=0.7 $ $ \alpha=\beta=0.001, \xi=0.5 $ $ l=24. $ -
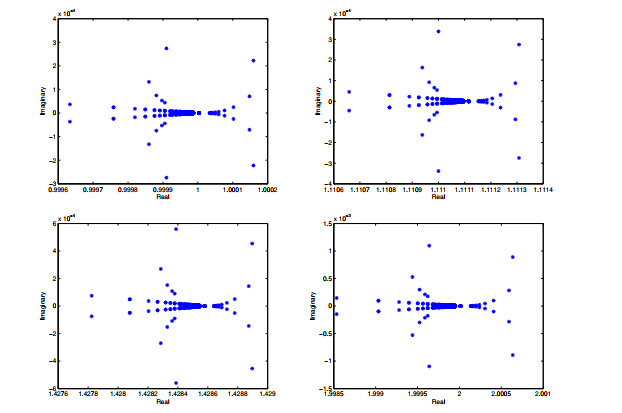
Figure 4.
The eigenvalue distribution for the parameter shift-splitting preconditioned matrix
$ \mathcal{T}_{PSS}^{-1}\mathcal {A} $ $ \alpha=\beta=0.001, \xi=0.5 $ $ \alpha=\beta=0.001, \xi=0.3 $ $ \alpha=\beta=0.001, \xi=0.1 $ $ \alpha=\beta=0.001, \xi=1.3 $ $ l=24. $