| Citation: |
Ali Khalouta. THE STUDY OF NONLINEAR FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS VIA THE KHALOUTA-ATANGANA-BALEANU OPERATOR[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3175-3196. doi: 10.11948/20230483
|
THE STUDY OF NONLINEAR FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS VIA THE KHALOUTA-ATANGANA-BALEANU OPERATOR
-
Abstract
This paper studies nonlinear fractional partial differential equations via the Khalouta-Atangana-Baleanu operator. Using Banach's fixed point theorem we obtain new results on the existence and uniqueness of solutions to the proposed problem. Furthermore, two new semi-analytical methods called Khalouta homotopy perturbation method (KHHPM) and Khalouta variational iteration method (KHVIM) are presented to find new approximate analytical solutions to our nonlinear fractional problem. The first of the two new proposed methods, KHHPM, is a hybrid method that combines homotopy perturbation method and Khalouta transform in the sense of Atangana-Baleanu-Caputo derivative. The other method, KHVIM is also a hybrid method that combines variational iteration method and Khalouta transform in the sense of Atangana-Baleanu-Caputo derivative. Convergence and absolute error analysis of KHHPM and KHVIM were also performed. A numerical example is provided to support our results. The results obtained showed that the proposed methods are very impressive, effective, reliable, and easy methods for dealing with complex problems in various fields of applied sciences and engineering.
-
-
References
[1] I. Alhribat and M. H. Samuh, Generating statistical distributions using fractional differential equations, Jordan Journal of Mathematics and Statistics, 2023, 16(2), 379–396. [2] G. Alotta, M. Di Paola and F. P. Pinnola, An unified formulation of strong non-local elasticity with fractional order calculus, Meccanica, 2022, 57, 793–805. doi: 10.1007/s11012-021-01428-x [3] A. Atangana and D. Baleanu, New fractional derivatives with non-local and non-singular kernel theory and application to heat transfer model, Thermal Science, 2016, 20(2), 763–769. doi: 10.2298/TSCI160111018A [4] R. Dhayal, M. Malik and S. Abbas, Solvability and optimal controls of non-instantaneous impulsive stochastic fractional differential equation of order $q\in (1, 2)$, Stochastics, 2021, 93(5), 780–802. doi: 10.1080/17442508.2020.1801685 [5] A. Giusti, On infinite order differential operators in fractional viscoelasticity, Fractional Calculus and Applied Analysis, 2017, 20(4), 854–867. DOI: 10.1515/fca-2017-0045. [6] P. A. Harris and R. Garra, Nonlinear heat conduction equations with memory: Physical meaning and analytical results, Journal of Mathematical Physics, 2017, 58(6), 063501. DOI: 10.1063/1.4984583. [7] J. H. He, Homotopy perturbation technique, Computer Methods in Applied Mechanics and Engineering, 1999, 178(3), 25–262. [8] J. H. He, Variational iteration method a kind of non linear analytical technique: Some exemples, International Journal of Non-Linear Mechanics, 1999, 34, 699–708. doi: 10.1016/S0020-7462(98)00048-1 [9] C. Ionescu, A. Lopes, D. Copot, J. A. T. Machado and J. H. T. Bates, The role of fractional calculus in modeling biological phenomena: A review, Communications in Nonlinear Science and Numerical Simulation, 2017, 51, 141–159. doi: 10.1016/j.cnsns.2017.04.001 [10] A. Khalouta, A new exponential type kernel integral transform: Khalouta transform and its applications, Mathematica Montisnigri, 2023, 57, 5–23. DOI: 10.20948/mathmontis-2023-57-1. [11] A. Khalouta, A new analytical series solution with convergence for nonlinear fractional Lienard's equations with Caputo fractional derivative, Kyungpook Mathematical Journal, 2022, 62, 583–593. [12] A. Khalouta, A novel iterative method to solve nonlinear wave-like equations of fractional order with variable coefficients, Revista Colombiana de Matematicas, 2022, 56(1), 13–34. doi: 10.15446/recolma.v56n1.105612 [13] A. Khalouta, New approaches for solving Caputo time-fractional nonlinear system of equations describing the unsteady flow of a polytropic gas, International Journal of Nonlinear Analysis and Applications, 2023, 14(3), 33–46. [14] A. Khalouta, A novel computational method for solving the fractional SIS epidemic model of two different fractional operators, Annals of the University of Craiova, Mathematics and Computer Science Series, 2023, 50(1), 136–151. [15] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and Application of Fractional Differential Equations, Elsevier, Amsterdam, 2006. [16] K. B. Oldham, Fractional differential equations in electrochemistry, Advances in Engineering Software, 2010, 41(1), 9–12. doi: 10.1016/j.advengsoft.2008.12.012 [17] R. Ozarslan, E. Bas, D. Baleanu and B. Acay, Fractional physical problems including wind-influenced projectile motion with Mittag-Leffler kernel, AIMS Mathematics, 2020, 5(1), 467–481. doi: 10.3934/math.2020031 [18] J. C. Prajapati, A. D. Patel, K. N. Pathak and A. K. Shukla, Fractional calculus approach in the study of instability phenomenon in fluid dynamics, Palestine Journal of Mathematics, 2012, 1(2), 95–103. [19] Z. U. Rehman, S. Boulaaras, R. Jan, I. Ahmad and S. Bahramand, Computational analysis of financial system through non-integer derivative, Journal of Computational Science, 2024, 75, 102204. [20] B. Shiria and D. Baleanu, Numerical solution of some fractional dynamical systems in medicine involving non-singular kernel with vector order, Results in Nonlinear Analysis, 2019, 2(4), 160–168. [21] J. Singh, D. Kumar and D. Baleanu, On the analysis of chemical kinetics system pertaining to a fractional derivative with Mittag-Leffler type kernel, Chaos, 2017, 27, 103113. [22] A. Traore and N. Sene, Model of economic growth in the context of fractional derivative, Alexandria Engineering Journal, 2020, 59(6), 4843–4850. [23] V. V. Uchaikin, Fractional Derivatives for Physicists and Engineers, Berlin, Springer, 2013. [24] G. C. Wu, Challenge in the variational iteration method–A new approach to identification of the lagrange multipliers, Journal of King Saud University-Science, 2013, 25(2), 175–178. [25] X. Yang, J. Zeng, C. Xu, L. Peng and J. Alsultan, Modeling of fractional differential equation in cloud computing image fusion algorithm, Applied Mathematics and Nonlinear Sciences, 2023, 8(1), 1125–1134. -
-
Figures(3) / Tables(2)
Export File
Citation
Ali Khalouta. THE STUDY OF NONLINEAR FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS VIA THE KHALOUTA-ATANGANA-BALEANU OPERATOR[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3175-3196. doi: 10.11948/20230483
Format
Content
DownLoad:
-
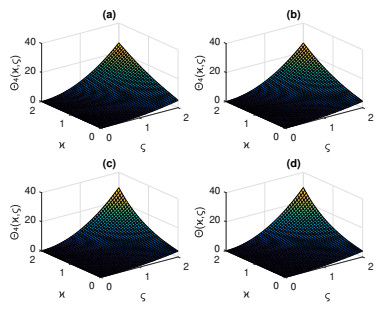
Figure 1.
3D plots of the approximate KHHPM-solutions for different values of
$ \alpha $ $ \alpha=0.8 $ $ \alpha=0.9 $ $ \alpha=1 $ -
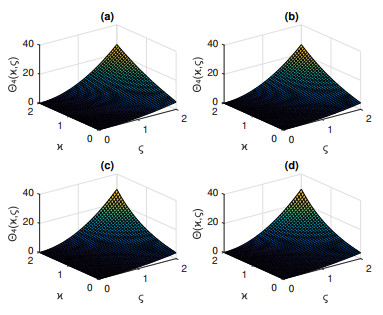
Figure 2.
3D plots of the approximate KHVIM-solutions for different values of
$ \alpha $ $ \alpha=0.8 $ $ \alpha=0.9 $ $ \alpha=1 $ -
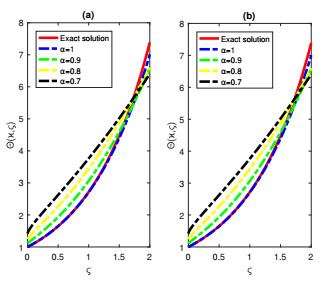
Figure 3.
2D plots of the approximate KHHPM-solutions, KHVIM-solutions and exact solution for different values of
$ \alpha $ $ \varkappa=0.5 $