| Citation: |
Azam Ghasemi, Abbas Saadatmandi. A BERNOULLI-REPRODUCING KERNEL METHOD FOR A CLASS OF NONLINEAR SINGULAR BOUNDARY VALUE PROBLEMS[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3260-3281. doi: 10.11948/20230508
|
A BERNOULLI-REPRODUCING KERNEL METHOD FOR A CLASS OF NONLINEAR SINGULAR BOUNDARY VALUE PROBLEMS
-
Abstract
We have developed a highly accurate numerical method called Bernoulli-RKM to solve nonlinear singular boundary value problems (SBVPs). This approach uses Bernoulli polynomials and the traditional reproducing kernel method (RKM) and applies the quasi-linearization method to linearize the SBVPs. We have discussed the error and convergence of Bernoulli-RKM and provided numerical examples to demonstrate its potential in solving nonlinear SBVPs. Additionally, we have compared our results with those in existing literature.
-
-
References
[1] E. Babolian, A. Eftekhari and A. Saadatmandi, A Sinc-Galerkin technique for the numerical solution of a class of singular boundary value problems, Comp. Appl. Math., 2015, 34, 45–63. doi: 10.1007/s40314-013-0103-x [2] M. Bagherzadeh and A. Neamaty, The Borg's theorem for singular Sturm-Liouville problem with non-separated boundary conditions, Math. Interdisc. Res., 2023, 8(3), 233–245. [3] S. H. Chang, Electroosmotic flow in a dissimilarly charged slit microchannel containing salt-free solution, Eur. J. Mech. B Fluids., 2012, 34, 85–90. doi: 10.1016/j.euromechflu.2012.01.020 [4] S. H. Chang, A variational iteration method involving Adomian polynomials for a strongly nonlinear boundary value problem, East Asian J. Appl. Math., 2019, 9(1), 153–164. doi: 10.4208/eajam.041116.291118 [5] Z. Chen, W. Jiang and H. Du, A new reproducing kernel method for Duffing equations, Int. J. Comput. Math., 2021, 98(11), 2341–2354. doi: 10.1080/00207160.2021.1897111 [6] M. Cui and Y. Lin, Nonlinear Numerical Analysis in the Reproducing Kernel Space, Nova Science Publishers, Inc, 2009. [7] M. Danish, S. Kumar and S. Kumar, A note on the solution of singular boundary value problems arising in engineering and applied sciences: Use of OHAM, Comput. Chem. Eng., 2012, 36, 57–67. doi: 10.1016/j.compchemeng.2011.08.008 [8] M. Dehghan and A. Nikpour, Numerical solution of the system of second-order boundary value problems using the local radial basis functions based differential quadrature collocation method, Appl. Math. Model., 2013, 37(18–19), 8578–8599. [9] M. Dehghan and F. Shakeri, Asemi-numerical technique for solving the multi-point boundary value problems and engineering applications, Int. J. Numer. Methods Heat Fluid Flow, 2011, 21(7), 794–809. doi: 10.1108/09615531111162783 [10] M. Dehghan and M. Tatari, Finding approximate solutions for a class of third-order non-linear boundary value problems via the decomposition method of Adomian, Int. J. Comput. Math., 2010, 87(6), 1256–1263. doi: 10.1080/00207160802270853 [11] F. Deutsch, Best Approximation in Inner Product Spaces, Springer, New York, 2001. [12] A. Eftekhari, Spectral poly-sinc collocation method for solving a singular nonlinear BVP of reaction-diffusion with Michaelis-Menten kinetics in a catalyst/biocatalyst, Iranian J. Math. Chem., 2023, 14(2), 77–96. [13] A. Eftekhari and A. Saadatmandi, DE sinc-collocation method for solving a class of second-order nonlinear BVPs, Math. Interdisc. Res., 2021, 6(1), 11–22. doi: 10.3126/ire.v6i1.43413 [14] S. Farzaneh Javan, S. Abbasbandy and M. A. Fariborzi Araghi, Application of reproducing kernel Hilbert space method for solving a class of nonlinear integral equations, Math. Probl. Eng., 2017, 2017(1), 7498136. [15] B. F. Gray, The distribution of heat sources in the human head-theoretical consideration, J. Theor. Biol., 1980, 82(3), 473–476. doi: 10.1016/0022-5193(80)90250-7 [16] J. Guo, A. Khan, M. Sulaiman and P. Kumam, A novel neuroevolutionary naradigm for solving strongly nonlinear singular boundary value vroblems in physiology, IEEE Access, 2022, 10, 21979–22002. doi: 10.1109/ACCESS.2022.3152193 [17] A. R. Kanth and V. Bhattacharya, Cubic spline for a class of non-linear singular boundary value problems arising in physiology, Appl. Math. Comput., 2006, 174(1), 768–774. [18] M. Lakestani and M. Dehghan, Four techniques based on the B-spline expansion and the collocation approach for the numerical solution of the Lane-Emden equation, Math. Methods Appl. Sci., 2013, 36(16), 2243–2253. doi: 10.1002/mma.2755 [19] S. H. Lin, Oxygen diffusion in a spherical cell with nonlinear oxygen uptake kinetics, J. Theor. Biol., 1976, 60(2), 449–457. doi: 10.1016/0022-5193(76)90071-0 [20] C. S. Liu, E. R. El-Zahar and C. W. Chang, A boundary shape function iterative method for solving nonlinear singular boundary value problems, Math. Comput. Simul., 2021, 187, 614–629. doi: 10.1016/j.matcom.2021.03.030 [21] V. B. Mandelzweig and F. Tabakin, Quasilinearization approach to nonlinear problems in physics with application to nonlinear ODEs, Comput. Phys. Commun., 2001, 141(2), 268–281. doi: 10.1016/S0010-4655(01)00415-5 [22] S. Mashayekhi, Y. Ordokhani and M. Razzaghi, Hybrid functions approach for optimal control of systems described by integro-differential equations, Appl. Math. Model., 2013, 37(5), 3355–3368. doi: 10.1016/j.apm.2012.07.014 [23] D. B. Meade, B. S. Haran and R. E. White, The shooting technique for the solution of two-point boundary value problems, Maple Tech. Newsl., 1996, 3(1), 1–8. [24] F. Mirzaee and N. Samadyar, Explicit representation of orthonormal Bernoulli polynomials and its application for solving Volterra-Fredholm-Hammerstein integral equations, SeMA J., 2020, 77(1), 81–96. doi: 10.1007/s40324-019-00203-z [25] M. Mohsenyzadeh, K. Maleknejad and R. Ezzati, A numerical approach for the solution of a class of singular boundary value problems arising in physiology, Adv. Differ. Equ., 2015, 2015, 1–10. doi: 10.1186/s13662-014-0331-4 [26] J. Niu, M. Xu, Y. Lin and Q. Xue, Numerical solution of nonlinear singular boundary value problems, J. Comput. Appl. Math., 2018, 331, 42–51. doi: 10.1016/j.cam.2017.09.040 [27] R. K. Pandey and S. Tomar, An effective scheme for solving a class of nonlinear doubly singular boundary value problems through quasilinearization approach, J. Comput. Appl. Math., 2021, 392, 113411. doi: 10.1016/j.cam.2021.113411 [28] R. K. Pandey and A. K. Verma, Existence-uniqueness results for a class of singular boundary value problems arising in physiology, Nonlinear Anal. : Real World Appl., 2008, 9(1), 40–52. doi: 10.1016/j.nonrwa.2006.09.001 [29] K. Parand, A. Ghaderi-Kangavari and M. Delkosh, Two efficient computational algorithms to solve the nonlinear singular Lane-Emden equations, Astrophysics, 2020, 63(1), 133–150. doi: 10.1007/s10511-020-09621-8 [30] M. Pourbabaee and A. Saadatmandi, New operational matrix of Riemann-Liouville fractional derivative of orthonormal Bernoulli polynomials for the numerical solution of some distributed-order time-fractional partial differential equations, J. Appl. Anal. Comput., 2023, 13(6), 3352–3373. [31] P. Roul, On the numerical solution of singular two-point boundary value problems: A domain decomposition homotopy perturbation approach, Math. Methods Appl. Sci., 2017, 40(18), 7396–7409. doi: 10.1002/mma.4536 [32] P. Roul, A fast and accurate computational technique for efficient numerical solution of nonlinear singular boundary value problems, Int. J. Comput. Math., 2019, 96(1), 51–72. doi: 10.1080/00207160.2017.1417588 [33] P. Roul, Doubly singular boundary value problems with derivative dependent source function: A fast-converging iterative approach, Math. Methods Appl. Sci., 2019, 42(1), 354–374. doi: 10.1002/mma.5351 [34] P. Roul, A new mixed MADM-collocation approach for solving a class of Lane-Emden singular boundary value problems, J. Math. Chem., 2019, 57, 945–969. doi: 10.1007/s10910-018-00995-x [35] P. Roul, A fourth-order non-uniform mesh optimal B-spline collocation method for solving a strongly nonlinear singular boundary value problem describing electrohydrodynamic flow of a fluid, Appl. Numer. Math., 2020, 153, 558–574. doi: 10.1016/j.apnum.2020.03.018 [36] P. Roul and V. P. Goura, Numerical solution of doubly singular boundary value problems by finite difference method, Comp. Appl. Math., 2020, 39, 1–25. doi: 10.1007/s40314-019-0964-8 [37] P. Roul, V. P. Goura and R. Agarwal, A compact finite difference method for a general class of nonlinear singular boundary value problems with Neumann and Robin boundary conditions, Appl. Math. Comput., 2019, 350, 283–304. [38] P. Roul and H. Madduri, A new highly accurate domain decomposition optimal homotopy analysis method and its convergence for singular boundary value problems, Math. Methods Appl. Sci., 2018, 41(16), 6625–6644. doi: 10.1002/mma.5181 [39] P. Roul, H. Madduri and K. Kassner, A new iterative algorithm for a strongly nonlinear singular boundary value problem, J. Comput. Appl. Math., 2019, 351, 167–178. doi: 10.1016/j.cam.2018.10.043 [40] P. Roul, H. Madduri and K. Kassner, A sixth-order numerical method for a strongly nonlinear singular boundary value problem governing electrohydrodynamic flow in a circular cylindrical conduit, Appl. Math. Comput., 2019, 350, 416–433. [41] P. Roul, K. Thula and R. Agarwal, Non-optimal fourth-order and optimal sixth-order B-spline collocation methods for Lane-Emden boundary value problems, Appl. Numer. Math., 2019, 145, 342–360. doi: 10.1016/j.apnum.2019.05.004 [42] A. Saadatmandi, N. Nafar and S. P. Toufighi, Numerical study on the reaction cum diffusion process in a spherical biocatalyst, Iranian J. Math. Chem., 2014, 5, 47–61. [43] M. G. Sakar, O. Saldlr and A. Akgül, Numerical solution of fractional Bratu type equations with Legendre reproducing kernel method, Int. J. Appl. Comput. Math., 2018, 4(5), 126. doi: 10.1007/s40819-018-0562-2 [44] J. Shen, T. Tang and L. Wang, Spectral Methods: Algorithms, Analysis and Applications, Springer, 2011. [45] R. Singh and J. Kumar, An efficient numerical technique for the solution of nonlinear singular boundary value problems, Comput. Phys. Commun., 2014, 185(4), 1282–1289. doi: 10.1016/j.cpc.2014.01.002 [46] Umesh and M. Kumar, Numerical solution of singular boundary value problems using advanced Adomian decomposition method, Eng. Comput., 2021, 37, 2853–2863. doi: 10.1007/s00366-020-00972-6 [47] L. J. Xie, C. L. Zhou and S. Xu, An effective numerical method to solve a class of nonlinear singular boundary value problems using improved differential transform method, SpringerPlus, 2016, 5, 1–19. doi: 10.1186/s40064-015-1659-2 [48] M. Xu and E. Tohidi, A Legendre reproducing kernel method with higher convergence order for a class of singular two-point boundary value problems, J. Appl. Math. Comput, 2021, 67, 405–421. doi: 10.1007/s12190-020-01494-6 [49] Y. H. Youssri, S. M. Sayed, A. S. Mohamed, E. M. Aboeldahab and W. M. Abd-Elhameed, Modified Lucas polynomials for the numerical treatment of second-order boundary value problems, Comput. Methods Differ. Equ., 2023, 11(1), 12–31. [50] S. Zaremba, Sur le calcul numerique des founctions demandess dans le problems de dirichlet et le problems hydrodynamique, Bull. Int. Acad. Sci. Cracovie, 1908, 68, 125–195. [51] H. Zhu, J. Niu, R. Zhang and Y. Lin, A new approach for solving nonlinear singular boundary value problems, Math. Model. Anal., 2018, 23(1), 33–43. doi: 10.3846/mma.2018.003 -
-
Figures(9) / Tables(10)
Export File
Citation
Azam Ghasemi, Abbas Saadatmandi. A BERNOULLI-REPRODUCING KERNEL METHOD FOR A CLASS OF NONLINEAR SINGULAR BOUNDARY VALUE PROBLEMS[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3260-3281. doi: 10.11948/20230508
Format
Content
DownLoad:
-
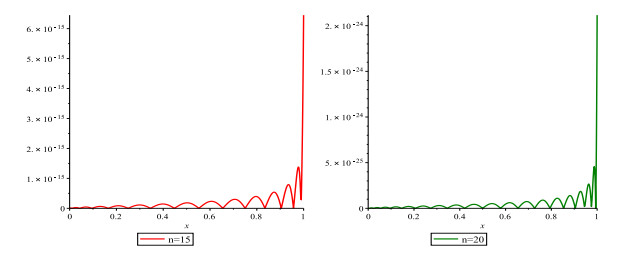
Figure 1.
Graph of
$ ER_{n, 1}(x) $ $ n=14 $ $ n=18 $ -
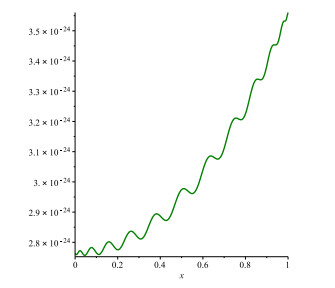
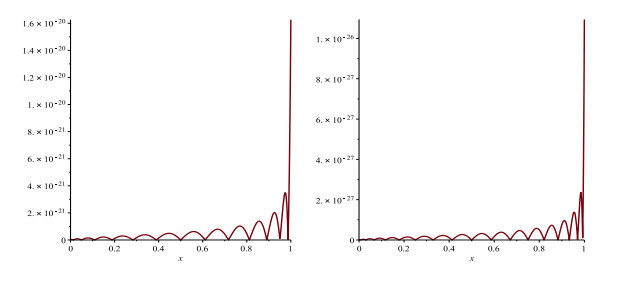
Figure 2.
Graph of
$ ER_{n, 3}(x) $ $ {\bf Case}\ 1 $ $ {\bf Case}\ 3 $ -
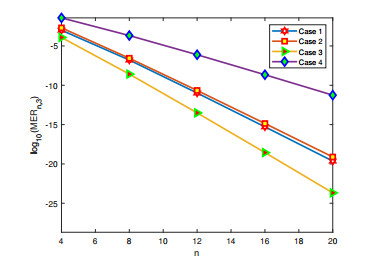
Figure 3.
Graph of
$ \log_{10}(MER_{n, 3}) $ $ n=4, 8, 12, 16, 20, $ -
Figure 4.
Graph of absolute error function
$ |\nu(x)-\nu_{n, 4}(x)| $ $ n=25 $ -
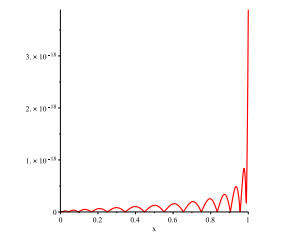
Figure 5.
Graph of
$ ER_{15, 1}(x) $ $ \varphi=2, $ $ m=0.5 $ -
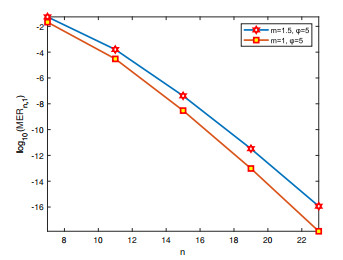
Figure 6.
Graph of
$ \log_{10}(MER_{n, 1}) $ $ n=7, 11, 15, 19, 23, $ -
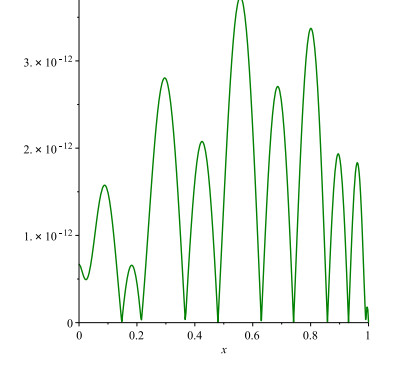
Figure 7.
Graph of absolute error function
$ |\nu(x)-\nu_{n, 4}(x)| $ $ n=12 $ -
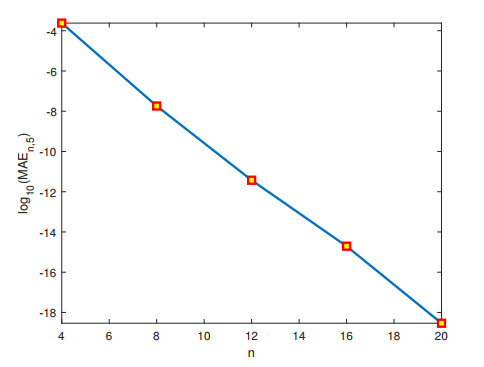
Figure 8.
Graph of
$ \log_{10}(MAE_{n, 5}) $ $ n=4, 8, 12, 16, 20, $ -
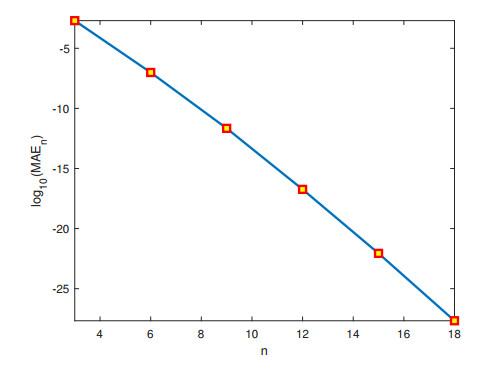
Figure 9.
Graph of
$ \log_{10}(MAE_{n}) $ $ n $