| Citation: |
Nazek A. Obeidat, Mahmoud S. Rawashdeh, Malak Q. Al Erjani. A NEW EFFICIENT TRANSFORM MECHANISM WITH CONVERGENCE ANALYSIS OF THE SPACE-FRACTIONAL TELEGRAPH EQUATIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(5): 3007-3032. doi: 10.11948/20240037
|
A NEW EFFICIENT TRANSFORM MECHANISM WITH CONVERGENCE ANALYSIS OF THE SPACE-FRACTIONAL TELEGRAPH EQUATIONS
-
Abstract
This article's goal is to investigate the space-fractional telegraph equation using an effective method called the Adomian natural decomposition method (ANDM), which is a combination of the Adomian decomposition method (ADM) and the natural transform method (NTM). Using the Banach fixed point theorem, we explore proofs for the existence and uniqueness theorems applying it to a nonlinear differential equation. Using our method, exact solutions of the space-fractional telegraph equation and time-fractional diffusion problems have been obtained. To demonstrate the effectiveness of the suggested scheme, four examples are provided.
-
-
References
[1] S. Al-Shara, Fractional transformation method for constructing solitary wave solutions to some nonlinear fractional partial differential equations, Applied Mathematical Sciences, 2014, 8(116), 5751–5762. [2] O. Alsayyed, F. Awawdeh, S. Al-Shara' and E. Rawashdeh, High-order schemes for nonlinear fractional differential equations, Fractal and Fractional, 2022, 6(12), 748. doi: 10.3390/fractalfract6120748 [3] O. P. Agrawal, Solution for a fractional diffusion-wave equation defined in a bounded domain, Nonlinear Dynamics, 2002, 29, 145–155. doi: 10.1023/A:1016539022492 [4] O. P. Agrawal, Response of a diffusion-wave system subjected to deterministic and stochastic fields, ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik: Applied Mathematics and Mechanics, 2003, 83(4), 265–274. [5] F. B. M. Belgacem and R. Silambarasan, Theory of natural transform, Math. Engg. Sci. Aeros., 2012, 3, 99–124. [6] I. L. El-Kalla, Convergence of Adomian's method applied to a class of Volterra type integro-differential equations, International Journal of Differential Equations and Applications, 2005, 10(2), 225–234. [7] H. Eltayeb, Y. T. Abdalla, I. Bachar and M. H. Khabir, Fractional telegraph equation and its solution by natural transform decomposition method, Symmetry, 2019, 11(3), 334. doi: 10.3390/sym11030334 [8] Y. Fujita, Cauchy problems of fractional order and stable processes, Japan journal of applied mathematics, 1990, 7, 459–476. [9] Y. Fujita, Integrodifferential equation which interpolates the heat equation and the wave equation, Osaka J. Math., 1990, 27, 309–321. [10] M. Garg and P. Manohar, Numerical solution of fractional diffusion-wave equation with two space variables by matrix method, Fractional Calculus and Applied Analysis, 2010, 13(2), 191–207. [11] M. Garg and A. Sharma, Solution of space-time fractional telegraph equation by Adomian decomposition method, Journal of Inequalities and Special Functions, 2011, 2(1), 1–7. [12] M. S. Hashmi, U. Aslam, J. Singh and K. S. Nisar, An efficient numerical scheme for fractional model of telegraph equation, Alexandria Engineering Journal, 2022, 61(8), 6383–6393. doi: 10.1016/j.aej.2021.11.065 [13] Z. Liu and S. Sun, Solvability and stability of multi-term fractional delay q-difference equation, Journal of Applied Analysis & Computation, 2024, 14(3), 1177–1197. [14] D. Loonker and P. K Banerji, Solution of fractional ordinary differential equations by natural transform, Int. J. Math. Eng. Sci., 2013, 12(2), 1–7. [15] Y. Luchko, Fractional wave equation and damped waves, Journal of Mathematical Physics, 2013, 54(3). [16] Y. Luchko, Wave–diffusion dualism of the neutral-fractional processes, Journal of Computational Physics, 2015, 293, 40–52. doi: 10.1016/j.jcp.2014.06.005 [17] Y. Luchko, F. Mainardi, Y. Povstenko, Propagation speed of the maximum of the fundamental solution to the fractional diffusion–wave equation, Computers & Mathematics with Applications, 2013, 66(5), 774–784. [18] S. M. Mabrouk, A. M. Wazwaz and A. S. Rashed, Monitoring dynamical behavior and optical solutions of space-time fractional order double-chain deoxyribonucleic acid model considering the Atangana's conformable derivative, Journal of Applied and Computational Mechanics, 2024. [19] F. Mainardi, Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models, World Scientific, 2022. [20] R. Metzler and J. Klafter, The random walk's guide to anomalous diffusion: A fractional dynamics approach, Physics reports, 2000, 339(1), 1–77. doi: 10.1016/S0370-1573(00)00070-3 [21] G. M. Mittag-Leffler, Sur la nouvelle fonction ${\mathbb E}_{\alpha } \left( \rm x \right)$, CR Acad. Sci. Paris, 1903, 137(2), 554–558. ${\mathbb E}_{\alpha } \left(\rm x \right)$" target="_blank">Google Scholar
[22] S. Momani, Analytic and approximate solutions of the space-and time-fractional telegraph equations, Applied Mathematics and Computation, 2005, 170(2), 1126–1134. doi: 10.1016/j.amc.2005.01.009 [23] N. A. Obeidat and D. E. Bentil, New theories and applications of tempered fractional differential equations, Nonlinear Dynamics, 2021, 105(2), 1689–1702. doi: 10.1007/s11071-021-06628-4 [24] N. A. Obeidat and D. E. Bentil, Novel technique to investigate the convergence analysis of the tempered fractional natural transform method applied to diffusion equations, Journal of Ocean Engineering and Science, 2023, 8(6), 636–646. doi: 10.1016/j.joes.2022.05.014 [25] E. Orsingher and X. Zhao, The space-fractional telegraph equation and the related fractional telegraph process, Chinese Annals of Mathematics, 2003, 24(1), 45–56. doi: 10.1142/S0252959903000050 [26] I. Podlubny, Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and some of their Applications, Elsevier, 1998. [27] A. Prakash, Analytical method for space-fractional telegraph equation by homotopy perturbation transform method, Nonlinear Engineering, 2016, 5(2), 123–128. [28] M. S. Rawashdeh, The fractional natural decomposition method: Theories and applications, Mathematical Methods in the Applied Sciences, 2017, 40(7), 2362–2376. doi: 10.1002/mma.4144 [29] M. S. Rawashdeh and H. Al-Jammal, New approximate solutions to fractional nonlinear systems of partial differential equations using the FNDM, Advances in Difference Equations, 2016, 1, 1–19. DOI: 10.1186/s13662-016-0960-2012-1. [30] M. S. Rawashdeh, N. A. Obeidat and H. S. Abedalqader, New class of nonlinear fractional integro-differential equations with theoretical analysis via fixed point approach: Numerical and exact solutions, Journal of Applied Analysis and Computation, 2023, 13(5), 2767–2787. [31] W. R. Schneider and W. Wyss, Fractional diffusion and wave equations, Journal of Mathematical Physics, 1989, 30(1), 134–144. doi: 10.1063/1.528578 [32] L. B. Shen and B. S. Han, Propagating terrace in a periodic reaction-diffusion equation with convection, Journal of Applied Analysis & Computation, 2024, 14(3), 1395–1413. -
-
Figures(12) / Tables(4)
Export File
Citation
Nazek A. Obeidat, Mahmoud S. Rawashdeh, Malak Q. Al Erjani. A NEW EFFICIENT TRANSFORM MECHANISM WITH CONVERGENCE ANALYSIS OF THE SPACE-FRACTIONAL TELEGRAPH EQUATIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(5): 3007-3032. doi: 10.11948/20240037
Format
Content
DownLoad:
-
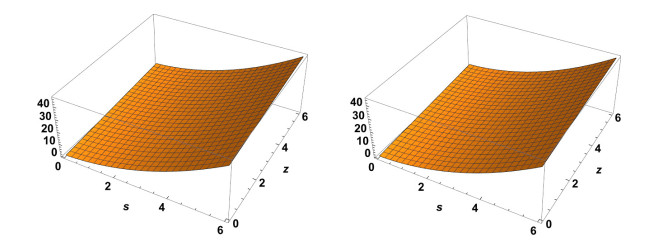
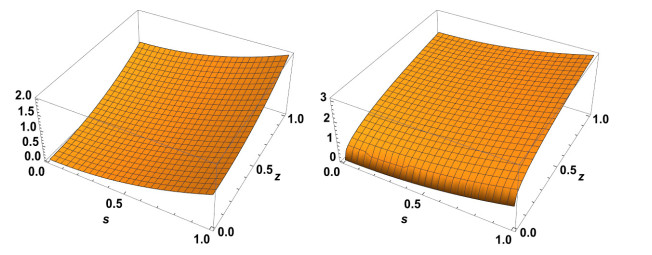
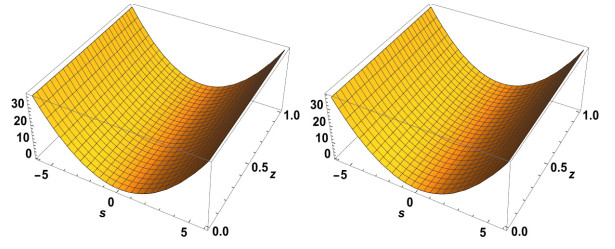
Figure 1.
Exact solution to
$ \chi(s,z) $ $ \alpha=2 $ $ \alpha=1.2 $ -
Figure 2.
Exact solution to
$ \chi(s,z) $ $ \alpha=1.4 $ $ \alpha=1.6 $ -
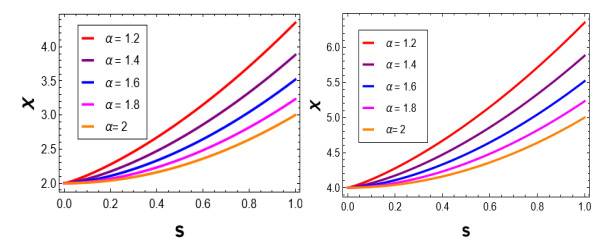
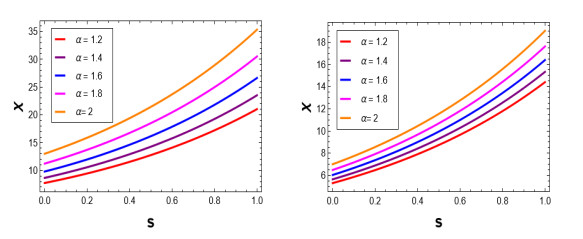
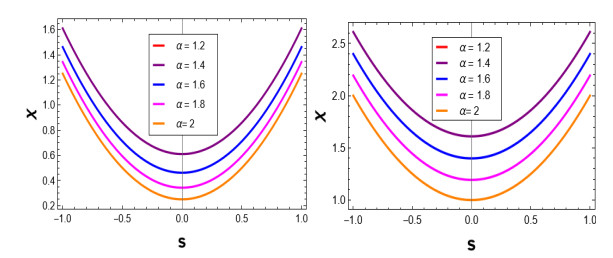
Figure 3.
Exact solution to
$ \chi(s,z) $ $ \alpha=1.2, 1.4, 1.6, 1.8, 2 $ $ z=2 $ $ z=4 $ -
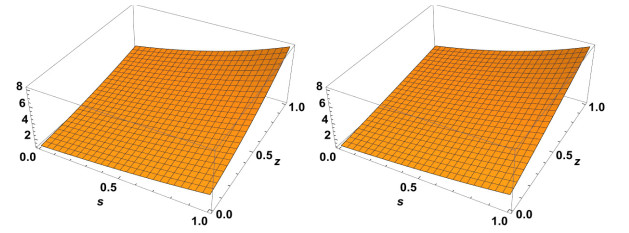
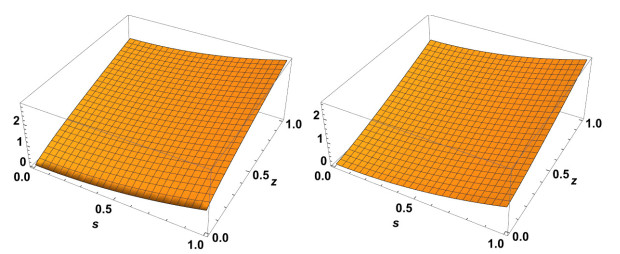
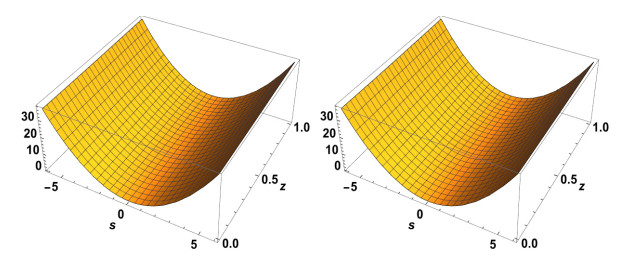
Figure 4.
Exact solution to
$ \chi(s,z) $ $ \alpha=2 $ $ \alpha=1.2 $ -
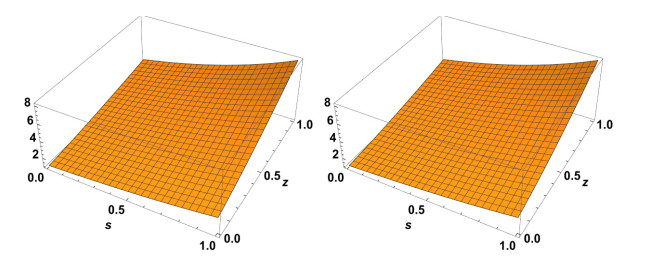
Figure 5.
Exact solution to
$ \chi(s,z) $ $ \alpha=1.4 $ $ \alpha=1.6 $ -
Figure 6.
Exact solution to
$ \chi(s,z) $ $ \alpha=1.2, 1.4, 1.6, 1.8, 2 $ $ z=2 $ $ z=3 $ -
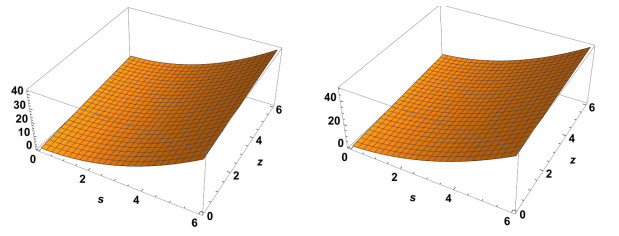
Figure 7.
Exact solution to
$ \chi(s,z) $ $ \alpha=2 $ $ \alpha=1.2 $ -
Figure 8.
Exact solution to
$ \chi(s,z) $ $ \alpha=1.4 $ $ \alpha=1.6 $ -
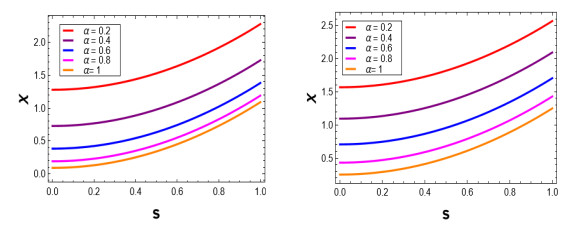
Figure 9.
Exact solution to
$ \chi(s,z) $ $ \alpha=0.2, 0.4, 0.6, 0.8, 1 $ $ z=0.3 $ $ z=0.5 $ -
Figure 10.
Exact solution to
$ \chi(s,z) $ $ \alpha=2 $ $ \alpha=1.2 $ $ k=1 $ -
Figure 11.
Exact solution to
$ \chi(s,z) $ $ \alpha=1.4 $ $ \alpha=1.6 $ $ k=1 $ -
Figure 12.
Exact solution to
$ \chi(s,z) $ $ \alpha=1.2, 1.4, 1.6, 1.8, 2 $ $ z=0.5 $ $ z=1 $ $ k=1 $