| Citation: |
A. M. S. Mahdy. NUMERICAL SOLUTION AND OPTIMAL CONTROL FOR FRACTIONAL TUMOR IMMUNE MODEL[J]. Journal of Applied Analysis & Computation, 2024, 14(5): 3033-3045. doi: 10.11948/20240053
|
NUMERICAL SOLUTION AND OPTIMAL CONTROL FOR FRACTIONAL TUMOR IMMUNE MODEL
-
Abstract
In this article, the numerical model of fractional tumor immunity has been described. The schematic of a signal flow of the structure model has been discussed. In the formulation of optimal control, the stability of this model at its equilibrium point will be studied. The error-estimated model has been studied. In addition to this, the optimal control of their form as well as the numerical approach for the simulation of the control problem, are both brought up and examined. The evidence that demonstrates has been presented the existence of the solution. An algorithm modelled after the generalized Adams-Bashforth-Moulton style (GABMS) has been used to solve the fractional tumor immune model. The memristor-based controlled form has been applied and proven to add a memristor impact as the returns code on the second scheme x2 of the main scheme. This amendment is predicated on changing the form to a memristive one for the first time because such a notion is being utilized for the first time to control this ailment. The dissection results have been interpreted using numerical simulations we created. To calculate the results has relied on the Maple 15 programming language.
-
Keywords:
- Fractional tumour immune /
- GABMS /
- optimal control /
- existence and uniqueness /
- memristive
-
-
References
[1] S. A. M. Abdelmohsen, D. Sh. Mohamed, H. A. Alyousef, M. R. Gorji and A. M. S. Mahdy, Mathematical modeling for solving fractional model cancer bosom malignant growth, AIMS Biophysics, 2023, 10(3), 263–280. doi: 10.3934/biophy.2023018 [2] W. Adel, Y. A. Amer, E. S. M. Youssef and A. M. S. Mahdy, Mathematical analysis and simulations for a Caputo-Fabrizio fractional COVID-19 model, Partial Differential Equations in Applied Mathematics, 2023, 8, 1–12. [3] R. P. Agarwal, A. M. A. El-Sayed and S. M. Salman, Fractional-order Chua system discretization, bifurcation and chaos, Advances in Difference Equations, 2013, 2013, 1–13. doi: 10.1186/1687-1847-2013-1 [4] E. Ahmed, A. Hashish and F. A. Rihan, On fractional order cancer model, Journal of Fractional Calculus and Applied Analysis, 2012, 3(2), 1–6. [5] A. A. M. Arafa, S. Z. Rida and M. Khalil, Fractional modeling dynamics of HIV and CD4+ T-cells during primary infection, Non-linear Biomedical Physics, 2012, 6(1), 1–7. doi: 10.1186/1753-4631-6-1 [6] N. Bellomo, A. Bellouquid, J. Nieto and J. Soler, Multiscale biological tissue models and flux-limited chemotaxis for multicellular growing systems, Mathematical Models and Methods in Applied Sciences, 2010, 20(7), 1179–1207. doi: 10.1142/S0218202510004568 [7] M. Cosnard and P. Fraigniaud, Finding the roots of a polynomial on an MIMD multicomputer, Parallel Computing, 1990, 15(1–3), 75–85. doi: 10.1016/0167-8191(90)90032-5 [8] K. Diethelm, J. Ford and A. Freed, Multi-order fractional differential equations and their numerical solution, Applied Mathematics and Computation, 2004, 154, 621–640. doi: 10.1016/S0096-3003(03)00739-2 [9] A. El-Mesady, A. Elsonbaty and W. Adel, On nonlinear dynamics of a fractional order monkeypox virus model, Chaos Solitons and Fractals, 2022, 164, 112716. doi: 10.1016/j.chaos.2022.112716 [10] A. El-Mesady, A. A. Elsadany, A. M. S. Mahdy and A. Elsonbaty, Nonlinear dynamics and optimal control strategies of a novel fractional-order Lumpy Skin disease model, Journal of Computational Science, 2024, 102286. [11] A. A. Elsadany and A. E. Matouk, Dynamical behaviors of fractional-order Lotka-Volterra predator-prey model and its discretization, Applied Mathematics and Computation, 2015, 49, 269–283. doi: 10.3969/j.issn.1006-6330.2015.03.002 [12] A. M. A. El-Sayed and S. M. Salman, On a discretization process of fractional order Riccati differential equation, Journal of Fractional Calculus and Application, 2013, 4, 251–259. [13] M. El-Shahed, J. J. Nieto, A. M. Ahmed and I. M. E. Abdelstar, Fractional-order model for biocontrol of the lesser date moth in palm trees and its discretization, Advances in Difference Equations, 2013, 2013, 1–16. doi: 10.1186/1687-1847-2013-1 [14] A. El-Sonbaty, M. Alharbi, A. El-Mesady and W. Adel, Dynamical analysis of a novel discrete fractional lumpy skin disease model, Partial Differential Equations in Applied Mathematics, 2024, 9, 1–12. [15] M. I. A. Fathoni, Gunardi, F. A. Kusumo and S. H. Hutajulu, Mathematical model analysis of breast cancer stages with side effects on heart in chemotherapy patients, in AIP Conference Proceedings, AIP Publishing LLC, 2019, 2192(1), 060007. [16] R. L. Fournier, Basic transport phenomena in biomedical engineering, New York: Taylor and Francis, 2007, 1–611. [17] A. Gokdogan, A. Yildirim and M. Merdan, Solving a fractional order model of HIV infection of CD+ Tcells, Mathematical and Computer Modelling, 2011, 54(9–10), 2132–2138. doi: 10.1016/j.mcm.2011.05.022 [18] M. Higazy, A. El-Mesady, A. M. S. Mahdy, S. Ullah and A. Al-Ghamdi, Numerical approximate solutions and optimal control on the deathly lassa hemorrhagic fever disease in pregnant women, Journal of Function Spaces, 2021, 2021, 1–15. [19] D. Kirschner and J. C. Panetta, Modeling immunotherapy of the tumor-immune interaction, Journal of Mathematical Biology, 1998, 37(3), 235–252. doi: 10.1007/s002850050127 [20] K. Kretzschmar, Cancer research using organoid technology, Journal of Molecular Medicine, 2021, 99, 501–515. doi: 10.1007/s00109-020-01990-z [21] Y. Liu, J. Roberts and Y. Yan, Detailed error analysis for a fractional Adams method with graded meshes, Numerical Algorithms, 2018, 36, 1195–1216. [22] A. M. S. Mahdy, Stability existence and uniqueness for solving fractional Glioblastoma multiforme using a Caputo–Fabrizio derivative, Mathematical Methods in the Applied Sciences, 2023, 1–18. DOI: 10.1002/mma.9038. [23] A. M. S. Mahdy, Y. A. Amer, M. S. Mohamed and E. S. M. Youssef, General fractional financial models of awareness with Caputo Fabrizio derivative, Advances in Mechanical Engineering, 2020, 12(11), 1–9. [24] A. M. S. Mahdy, K. A. Gepreel, Kh. Lotfy and A. A. El-Bary, A numerical method for solving the Rubella ailment disease model, International Journal of Modern Physics C, 2021, 32(7), 1–15. [25] A. M. S. Mahdy, M. Higazy and M. S. Mohamed, Optimal and memristor-based control of a non-linear fractional Tumor-Immune model, CMC: Computers, Materials and Continua, 2021, 67(3), 3463–3486. doi: 10.32604/cmc.2021.015161 [26] A. M. S. Mahdy, Kh. Lotfy and A. A. El-Bary, Use of optimal control in studying the dynamical behaviors of fractional financial awareness models, Soft Computing, 2022, 26, 3401–3409. doi: 10.1007/s00500-022-06764-y [27] A. M. S. Mahdy, M. S. Mohamed, A. Y. Al Amiri and K. A. Gepreel, Optimal control and spectral collocation method for solving smoking models, Intelligent Automation and Soft Computing, 2022, 31(2), 899–915. doi: 10.32604/iasc.2022.017801 [28] A. M. S. Mahdy, M. S. Mohamed, Kh. Lotfy, M. Alhazmi, A. A. El-Bary and M. H. Raddadi, Numerical solution and dynamical behaviors for solving fractional nonlinear rubella ailment disease model, Results in Physics, 2021, 24, 104091. doi: 10.1016/j.rinp.2021.104091 [29] M. S. Mohamed, S. K. Elagan, S. J. Almalki, M. R. Alharthi, M. F. El-Badawy, S. A. Najati and A. M. S. Mahdy, Optimal control and solving of cellular DNA cancer model, Applied Mathematics and Information Sciences, 2022, 16(1), 109–119. doi: 10.18576/amis/160111 [30] M. S. Petkovic, L. D. Petkovic and J. Duzunic, On an efficient method for simultaneous approximation of polynomial multiple roots, Applicable Analysis and Discrete Mathematics, 2014, 8, 73–94. [31] I. Podlubny, Fractional Differential Equations, Academic Press, New York, 1999. [32] F. A. Rihan, Numerical modeling of fractional-order biological systems, Abstract and Applied Analysis, 2013, 2013, 1–13. [33] F. A. Rihan, M. Safan, M. A. Abdeen and D. Abdel Rahman, Qualitative and computational analysis of a mathematical model for tumor-immune interactions, Journal of Applied Mathematics, 2012, 2012, 1–19. [34] W. M. Saltzman, Drug Delivery: Engineering Principal for Drug Therapy, New York: Oxford University Press, 2001. [35] M. Shams, N. A. Mir, N. Rafiq, A. O. Almatroud and S. Akram, On dynamics of iterative techniques for non-linear equation with application in engineering, Mathematical Problems in Engineering, 2020, 2020, 1–17. [36] N. H. Sweilam, S. M. Al-Mekhlafi and D. Baleanu, Optimal control for a fractional tuberculosis infection model including the impact of diabetes and resistant strains, Journal of Advanced Research, 2019, 17, 125–137. [37] R. Yafia, Hopf bifurcation in differential equations with delay for tumor-immune system competition model, SIAM Journal on Applied Mathematics, 2007, 67(6), 1693–1703. -
-
Figures(13)
Export File
Citation
A. M. S. Mahdy. NUMERICAL SOLUTION AND OPTIMAL CONTROL FOR FRACTIONAL TUMOR IMMUNE MODEL[J]. Journal of Applied Analysis & Computation, 2024, 14(5): 3033-3045. doi: 10.11948/20240053
Format
Content
DownLoad:
-
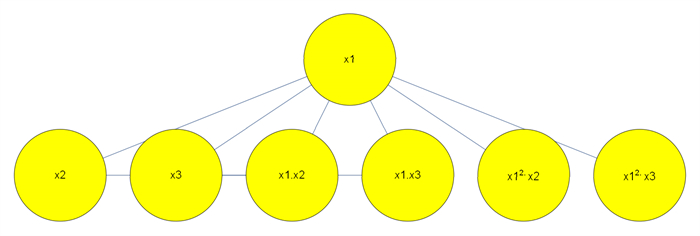
Figure 1.
The signal flow diagram of the structure model.
-
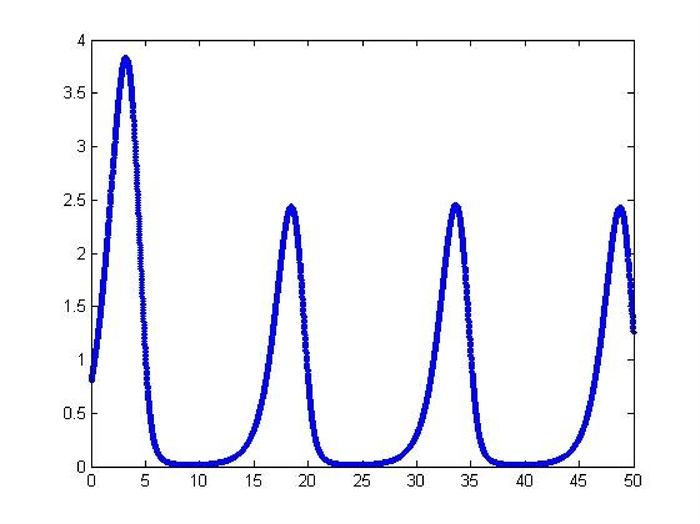
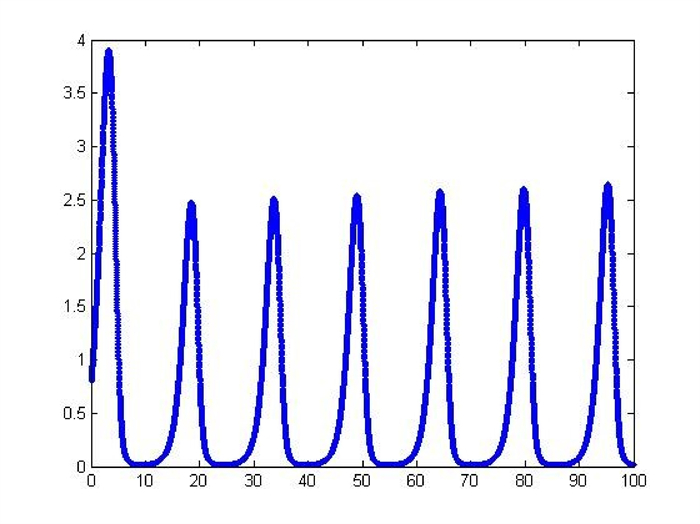
Figure 2.
The
$ x_{1} $ $ \epsilon=0.9. $ -
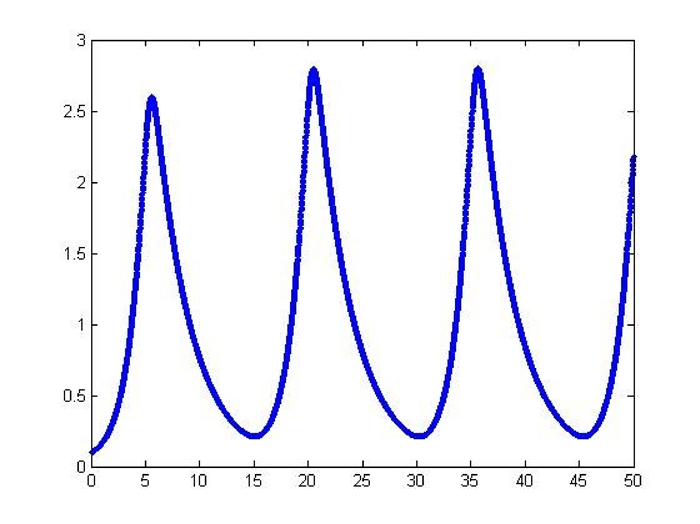
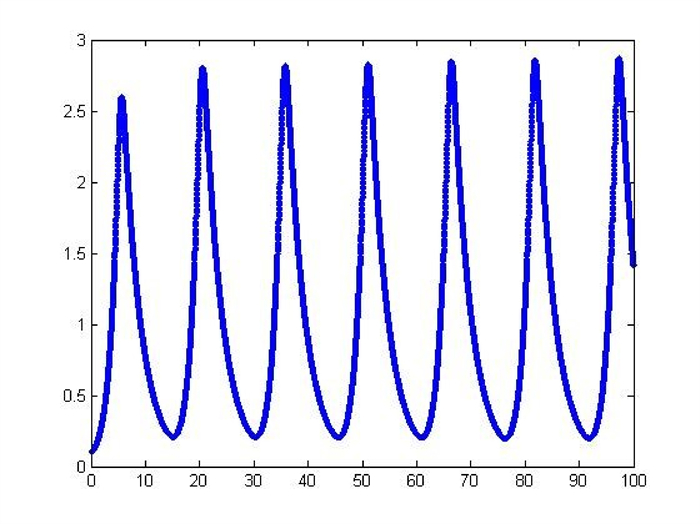
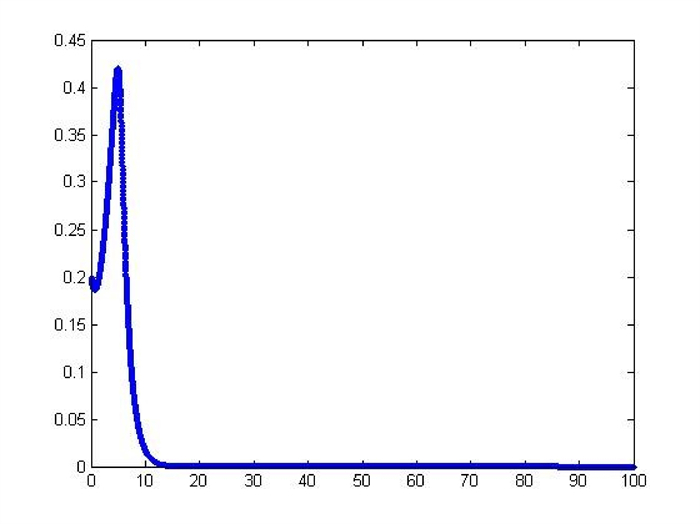
Figure 3.
The
$ x_{2} $ $ \epsilon=0.85. $ -
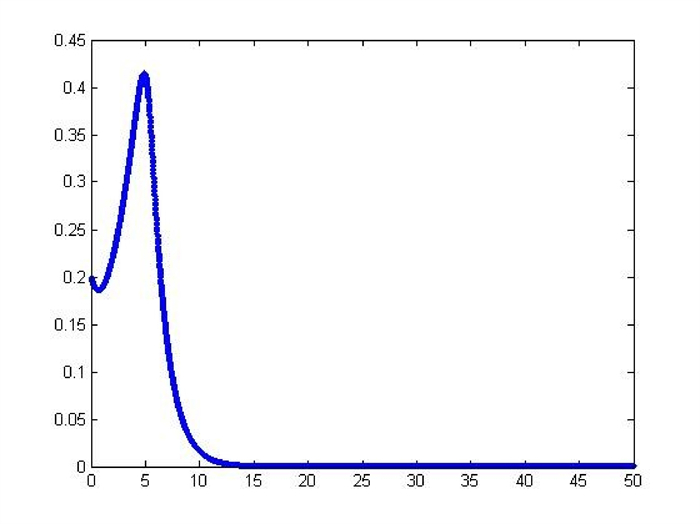
Figure 4.
The
$ x_{3} $ $ \epsilon=0.75. $ -
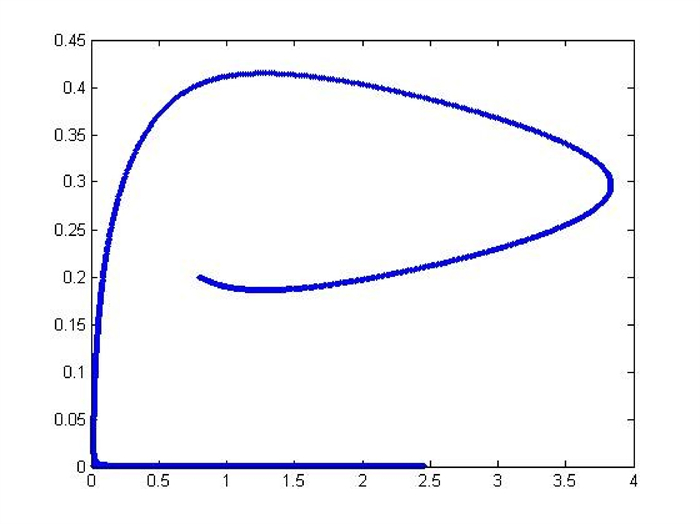
Figure 5.
The relation between
$ x_{1} $ $ x_{2} $ $ \epsilon=0.95. $ -
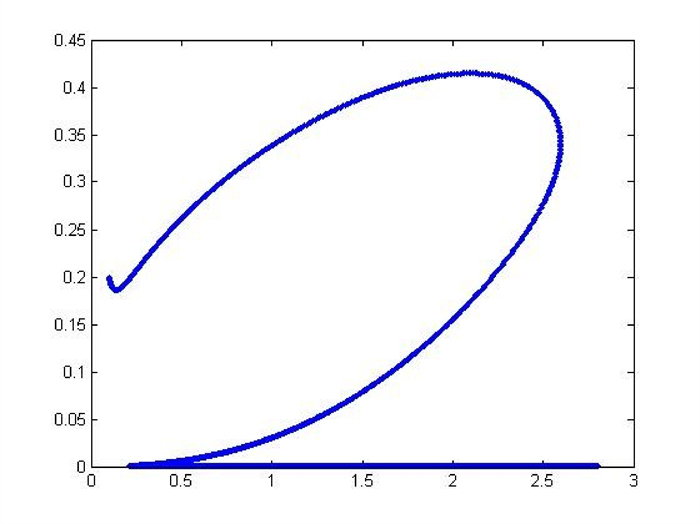
Figure 6.
The relation between
$ x_{1} $ $ x_{3} $ $ \epsilon=0.95. $ -
Figure 7.
The relation between
$ x_{2} $ $ x_{3} $ $ \epsilon=0.95. $ -
Figure 8.
The phase plane
$ x_{1} $ -
Figure 9.
The phase plane
$ x_{2} $ -
Figure 10.
The phase plane
$ x_{3} $ -
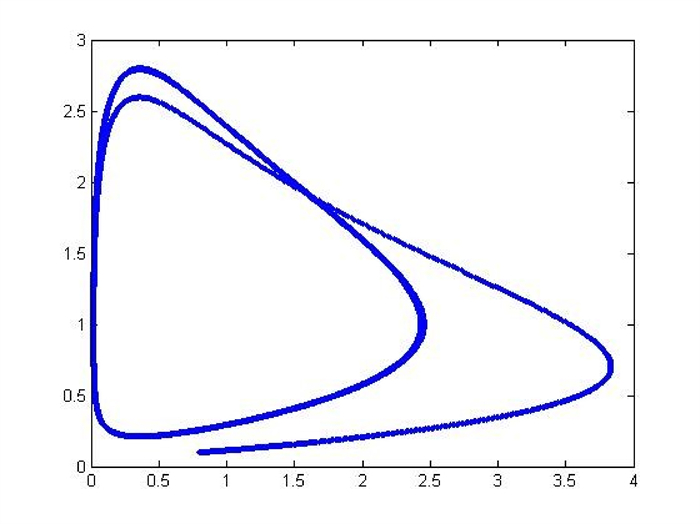
Figure 11.
The phase plane
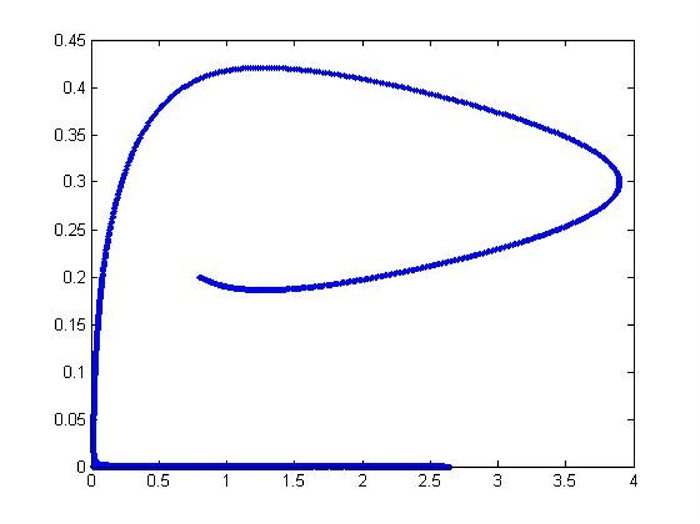
$ x_{1} $ $ x_{2} $ -
Figure 12.
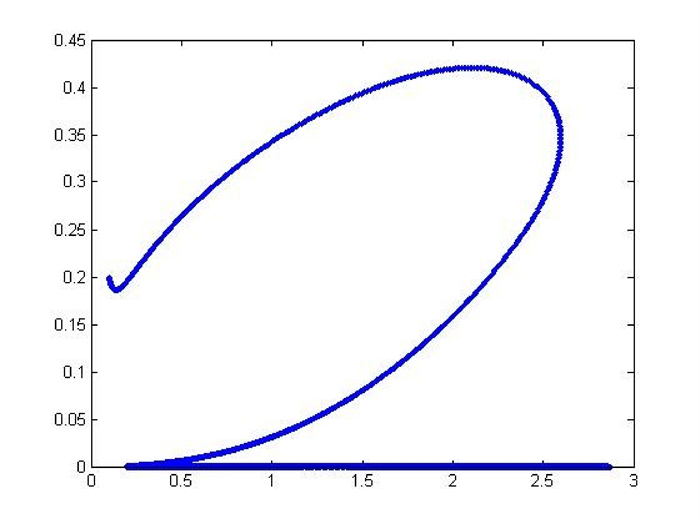
The phase plane
$ x_{1} $ $ x_{3} $ -
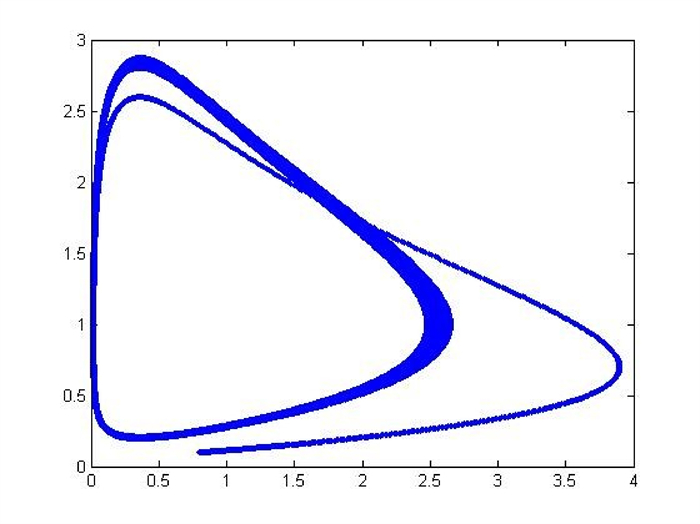
Figure 13.
The phase plane
$ x_{2} $ $ x_{3} $