| Citation: | Aissa Guesmia, Salim A. Messaoudi, Mostafa Zahri. GENERAL DECAY OF SOLUTIONS OF A WEAKLY COUPLED ABSTRACT EVOLUTION EQUATIONS WITH ONE FINITE MEMORY CONTROL[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3539-3557. doi: 10.11948/20240081 |
GENERAL DECAY OF SOLUTIONS OF A WEAKLY COUPLED ABSTRACT EVOLUTION EQUATIONS WITH ONE FINITE MEMORY CONTROL
-
Abstract
In this work, we consider the following abstract evolution system:
$ \begin{equation*} \left\{ \begin{array}{ll} u_{tt}(t)+Au(t)- \int_{0}^{t}g(t-s)A^{\theta }u(s)ds+\alpha v(t)=0, & t>0, \\ v_{tt}(t)+Av(t)+\alpha u(t)=0, & t>0, \\ u(0)=u_{0},\text{ }u_{t}(0)=u_{1},\text{ }v(0)=v_{0},\text{ }v_{t}(0)=v_{1},& \end{array} \right. \end{equation*} $
where $ A:\mathcal{D}(A)\subset H\longrightarrow H $ is a linear positive definite self-adjoint operator, $ H $ is a Hilbert space, $ g $ is a positive non-increasing function with some general decay rate, $ \theta\in \lbrack 0,1] $, $ \alpha $ is a positive constant and $ u_0 ,u_1 ,v_0 $ and $ v_1 $ are fixed initial data. Under appropriate conditions on $ g,\,\alpha $ and the regularity of the initial data, we establish a general decay rate of the solution energy which generalizes some earlier results in the literature. We, also, illustrated our results by performing several numerical tests.
-
Keywords:
- Coupled system /
- finite memory control /
- general decay /
- fractional operator
-

-
References
[1] M. Aassila, A note on the boundary stabilization of a compactly coupled system of wave equations, Appl. Math. Lett., 1999, 12, 19–24. [2] M. Aassila, Strong asymptotic stability of a compactly coupled system of wave equations, Appl. Math. Lett., 2001, 14, 285–290. doi: 10.1016/S0893-9659(00)00150-6 [3] M. Akil, H. Badawi, S. Nicaise and A. Wehbe, Stability results of coupled wave models with locally memory in a past history framework via nonsmooth coefficients on the interface, Math. Meth. Appl. Sci., 2021, 44, 6950–6981. doi: 10.1002/mma.7235 [4] F. Alabau, P. Cannarsa and V. Komornik, Indirect internal stabilization of weakly coupled evolution equations, J. Evol. Equa., 2002, 2, 127–150. doi: 10.1007/s00028-002-8083-0 [5] R. G. C. Almeida and M. L. Santos, Lack of exponential decay of a coupled system of wave equations with memory, Nonlinear Analysis: Real World Applications, 2011, 12, 1023–1032. doi: 10.1016/j.nonrwa.2010.08.025 [6] S. Boulaaras, R. Guefaia and N. Mezouar, Global existence and decay for a system of two singular one-dimensional nonlinear viscoelastic equations with general source terms, Appl. Anal., 2022, 101(3), 824–848. doi: 10.1080/00036811.2020.1760250 [7] M. M. Cavalcanti, V. N. Domingos Cavalcanti and A. Guesmia, Weak stability for coupled wave and/or Petrovsky systems with complementary frictional damping and infinite memory, J. Diff. Equa., 2015, 259, 7540–7577. doi: 10.1016/j.jde.2015.08.028 [8] S. M. S. Cordeiro, R. F. C. Lobato and C. A. Raposo, Optimal polynomial decay for a coupled system of wave with past history, Open J. Math. Anal., 2020, 4(1), 49–59. doi: 10.30538/psrp-oma2020.0052 [9] A. Draia, A. Zarai and S. Boulaaras, Global existence and decay of solutions of a singular nonlocal viscoelastic system, Rend. Circ. Mat. Palermo. Series 2, 2018, 1–25. [10] B. Feng, S. A. Messaoudi, A. Soufyane and M. Zahri, Optimal memory-type boundary control of the Bresse system, Asymptotic Analysis, 2022, 1–32. [11] A. Guesmia, Asymptotic behavior for coupled abstract evolution equations with one infinite memory, Applicable Analysis, 2015, 94, 184–217. doi: 10.1080/00036811.2014.890708 [12] K. L. Jin, J. Liang and T. J. Xiao, Coupled second order evolution equations with fading memory: Optimal energy decay rate, J. Diff. Equa., 2014, 257(5), 1501–1528. doi: 10.1016/j.jde.2014.05.018 [13] K. L. Jin, J. Liang and T. J. Xiao, Asymptotic behavior for coupled systems of second order abstract evolution equations with one infinite memory, J. Math. Anal. Appl., 2019, 475(1), 554–575. doi: 10.1016/j.jmaa.2019.02.055 [14] V. Komornik and R. Bopeng, Boundary stabilization of compactly coupled wave equations, Asymptotic Analysis, 1997, 14, 339–359. doi: 10.3233/ASY-1997-14403 [15] I. Lacheheb, S. A. Messaoudi and M. Zahri, Asymptotic stability of porous-elastic system with thermoelasticity of type Ⅲ, Arab. J. Math., 2021, 10, 137–155. doi: 10.1007/s40065-020-00305-x [16] R. F. C. Lobato, S. M. C. Cordeiro, M. L. Santos and D. S. Almeida Junior, Optimal polynomial decay to coupled wave equations and its numerical properties, J. Appl. Math., 2014, Art. ID 897080. [17] L. P. V. Matos, D. S. A. Junior and M. L. Santos, Polynomial decay to a class of abstract coupled systems with past history, Diff. Inte. Equa., 2012, 25, 1119–1134. [18] S. A. Messaoudi and W. Al-Khulaifi, General and optimal decay for a quasilinear viscoelastic equation, Appl. Math. Lett., 2017, 66, 16–22. DOI: 10.1016/j.aml.2016.11.002. [19] S. A. Messaoudi and M. Zahri, Analytical and computational results for the decay of solutions of a damped wave equation with variable-exponent nonlinearities, Topological Methods in Nonlinear Analysis, 2022, 59(2B), 851–866. [20] J. E. Muñoz Rivera and M. G. Naso, Asymptotic stability of semigroups associated with linear weak dissipative systems with memory, J. Math. Anal. Appl., 2007, 691–707. [21] J. E. Muñoz Rivera, M. G. Naso and F. M. Vegni, Asymptotic behavior of the energy for a class of weakly dissipative second-order systems with memory, J. Math. Anal. Appl., 2003, 286(2), 692–704. DOI: 10.1016/S0022-247X(03)00511-0. [22] M. Najafi, Study of exponential stability of coupled wave systems via distributed stabilizer, International Journal of Mathematics and Mathematical Sciences, 2001, 28, 479–491. doi: 10.1155/S0161171201003829 [23] R. L. Oliveira, H. P. Oquendo and C. Buriol, Exact decay rates for weakly coupled systems with indirect damping by fractional memory effects, Math. Nachr., 2023. DOI: 10.1002/mana.202100460. -
-
-
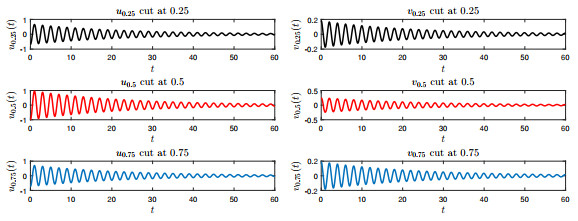
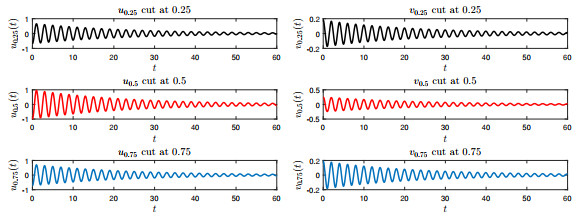
Figure 1.
Damping behavior of the waves
$ u $ $ v $ -
Figure 2.
Damping behavior of the waves
$ u $ $ v $ -
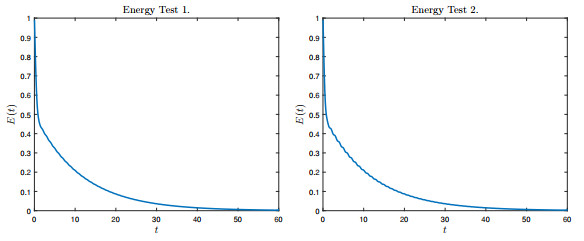
Figure 3.
Energy functions for Tests 1. and 2.
-
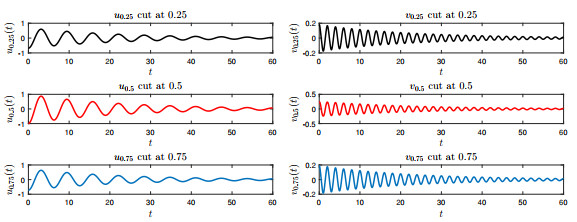
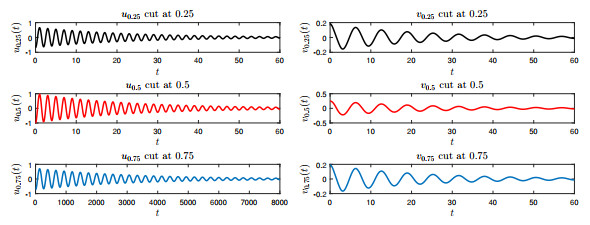
Figure 4.
Damping behavior of the waves
$ u $ $ v $ -
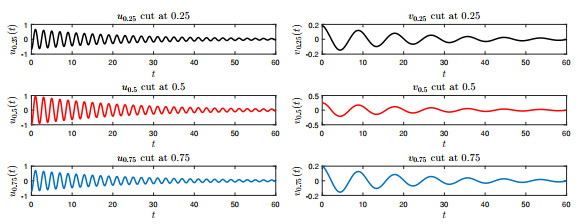
Figure 5.
Damping behavior of the waves
$ u $ $ v $ -
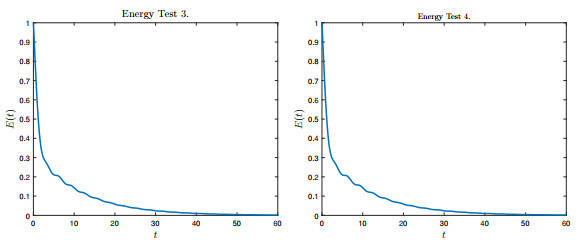
Figure 6.
Energy functions for Tests 3. and 4.
-
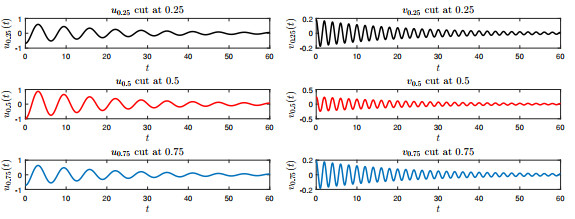
Figure 7.
Damping behavior of the waves
$ u $ $ v $ -
Figure 8.
Damping behavior of the waves
$ u $ $ v $ -
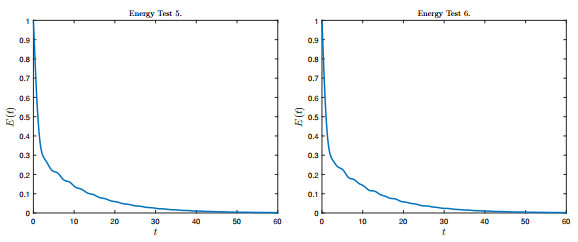
Figure 9.
Energy functions for Tests 5. and 6.




 DownLoad:
DownLoad: