| Citation: | Marc Jornet, Juan J. Nieto. PROPERTIES OF A NEW GENERALIZED CAPUTO-FABRIZIO FRACTIONAL DERIVATIVE[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3520-3538. doi: 10.11948/20240079 |
PROPERTIES OF A NEW GENERALIZED CAPUTO-FABRIZIO FRACTIONAL DERIVATIVE
-
Abstract
We investigate properties of a new fractional derivative recently introduced in the literature, which aims at generalizing the well-known Caputo-Fabrizio operator. We study the null space of the generalized derivative, the associated fractional integral operator, the null space of this integral, the validity of a fundamental theorem of calculus, the equivalence of integral problems with ordinary differential equations, the existence and uniqueness of solution for integral problems, and the form the nonsingular kernel should have to ensure consistency with the fractional order. A complete example with power input function is analyzed, which gives rise to a novel non-elementary solution and new dynamics in terms of the famous Lambert function.
-

-
References
[1] S. Abbas, M. Benchohra, J. E. Lazreg, J. J. Nieto and Y. Zhou, Fractional Differential Equations and Inclusions, Classical and Advanced Topics, World Scientific, Singapore, 2023. [2] T. Alinei-Poiana, E. H. Dulf and L. Kovacs, Fractional calculus in mathematical oncology, Sci. Rep., 2023, 13, Paper No. 10083, 14 pp. [3] A. S. Alshomrani, M. Z. Ullah and D. Baleanu, Caputo SIR model for COVID-19 under optimized fractional order, Adv. Differ. Equ., 2021, 2021(1), Paper No. 185, 17 pp. [4] I. Area, H. Batarfi, J. Losada, J. J. Nieto, W. Shammakh and Á. Torres, On a fractional order Ebola epidemic model, Adv. Differ. Equ., 2015, 2015(1), 1–12. doi: 10.1186/s13662-014-0331-4 [5] I. Area and J. J. Nieto, Fractional-order logistic differential equation with Mittag-Leffler-type kernel, Fractal Fract., 2021, 5(4), Paper No. 273, 13 pp. [6] I. Area and J. J. Nieto, On a quadratic nonlinear fractional equation, Fractal Fract., 2023, 7(6), Paper No. 469, 8 pp. [7] G. Ascione, Y. Mishura and E. Pirozzi, Fractional Deterministic and Stochastic Calculus, volume 4, De Gruyter Series in Probability and Stochastics, Walter de Gruyter, Berlin, 2024. [8] I. Baba and F. A. Rihan, A fractional-order model with different strains of COVID-19, Phys. A, 2022, 603, Paper No. 127813, 12 pp. [9] M. Bronstein, R. M. Corless, J. H. Davenport and D. J. Jeffrey, Algebraic properties of the Lambert W function from a result of Rosenlicht and of Liouville, Integral Transform. Spec. Funct., 2008, 19, 709–712. doi: 10.1080/10652460802332342 [10] M. Caputo and M. Fabrizio, A new definition of fractional derivative without singular kernel, Prog. Fract. Differ. Appl., 2015, 1, 73–85. [11] J. Čermák, T. Kisela and L. Nechvátal, The Lambert function method in qualitative analysis of fractional delay differential equations, Fract. Calc. Appl. Anal., 2023, 26, 1545–1565. doi: 10.1007/s13540-023-00176-x [12] I. Chatzigeorgiou, Bounds on the Lambert function and their application to the outage analysis of user cooperation, IEEE Communications Letters, 2013, 17(8), 1505–1508. doi: 10.1109/LCOMM.2013.070113.130972 [13] R. M. Corless, G. H. Gonnet, D. E. G. Hare, D. J. Jeffrey and D. E. Knuth, On the Lambert W function, Adv. Computational Math., 1996, 5(1), 329–359. doi: 10.1007/BF02124750 [14] C. A. Cruz-López and G. Espinosa-Paredes, Fractional radioactive decay law and Bateman equations, Nucl. Eng. Technol., 2022, 54(1), 275–282. doi: 10.1016/j.net.2021.07.026 [15] Z. Cui, Solutions of some typical nonlinear differential equations with Caputo-Fabrizio fractional derivative, AIMS Math., 2022, 7(8), 14139–14153. doi: 10.3934/math.2022779 [16] A. Granas and J. Dugundji, Fixed Point Theory, Springer-Verlag, New York, 2003. [17] M. Jornet, Power-series solutions of fractional-order compartmental models, Comput. Appl. Math., 2024, 43, Paper No. 67, 18 pp. [18] H. Joshi, B. K. Jha and M. Yavuz, Modelling and analysis of fractional-order vaccination model for control of COVID-19 outbreak using real data, Math. Bios. Eng., 2023, 20(1), 213–240. [19] S. Khajanchi, M. Sardar and J. J. Nieto, Application of non-singular kernel in a tumor model with strong Allee effect, Differ. Equ. Dyn. Syst., 2023, 31(3), 687–692. doi: 10.1007/s12591-022-00622-x [20] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and Applications of the Fractional Differential Equations, North-Holland Mathematics Studies, Elsevier, Amsterdam, 2006. [21] J. Losada and J. J. Nieto, Properties of a new fractional derivative without singular kernel, Prog. Fract. Differ. Appl., 2015, 1, 87–92. [22] J. Losada and J. J. Nieto, Fractional integral associated to fractional derivatives with nonsingular kernels, Prog. Fract. Differ. Appl., 2021, 7, 137–143. [23] F. Mainardi, E. Masina and J. L. González-Santander, A note on the Lambert W function: Bernstein and stieltjes properties for a creep model in linear viscoelasticity, Symmetry, 2023, 15(9), Paper No. 1654, 13 pp. [24] B. Melkamu and B. Mebrate, A fractional model for the dynamics of smoking tobacco using Caputo-Fabrizio derivative, J. Appl. Math., 2022, Paper No. 2009910, 10 pp. [25] F. Ndaïrou, I. Area, J. J. Nieto, C. J. Silva and D. F. Torres, Fractional model of COVID-19 applied to Galicia, Spain and Portugal, Chaos Soliton. Fract., 2021, 144, Paper No. 110652, 7 pp. [26] J. J. Nieto, Fractional Euler numbers and generalized proportional fractional logistic differential equation, Fract. Calc. Appl. Anal., 2022, 25(3), 876–886. doi: 10.1007/s13540-022-00044-0 [27] J. J. Nieto, Solution of a fractional logistic ordinary differential equation, Appl. Math. Lett., 2022, 123, Paper No. 107568, 5 pp. [28] A. Omame, M. Abbas and A. Abdel-Aty, Assessing the impact of SARS-CoV2 infection on the dynamics of dengue and HIV via fractional derivatives, Chaos Soliton. Fract., 2022, 162, Paper No. 112427, 22 pp. [29] M. Onitsuka and I. I. EL-Fassi, Generalized Caputo-Fabrizio fractional differential equation, J. Appl. Anal. Comput., 2024, 14(2), 964–975. [30] I. Podlubny, Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, 1st edn, Volume 198, Academic Press, New York, 1998. [31] D. Prodanov, Computational aspects of the approximate analytic solutions of the SIR model: Applications to modelling of COVID-19 outbreaks, Nonlinear Dyn., 2023, 111, 15613–15631. doi: 10.1007/s11071-023-08656-8 [32] J. Sabatier, Non-singular kernels for modelling power law type long memory behaviours and beyond, Cybernet. Syst., 2020, 51(4), 383–401. doi: 10.1080/01969722.2020.1758470 [33] J. Sabatier, Fractional state space description: A particular case of the Volterra equations, Fractal Fract., 2020, 4(2), Paper No. 23, 14 pp. [34] V. Tartaglione, C. Farges and J. Sabatier, Fractional behaviours modelling with Volterra equations: Application to a lithium-ion cell and comparison with a fractional model, Fractal Fract., 2022, 6(3), Paper No. 137, 14 pp. [35] Wolfram Research, Inc., Mathematica, Version 12.1, Champaign, IL, 2020. [36] B. Yang, Z. Luo, X. Zhang, Q. Tang and J. Liu, Trajectories and singular points of two-dimensional fractional-order autonomous systems, Adv. Math. Phys., 2022, Paper No. 3722011, 9 pp. [37] Z. Yong, Basic Theory of Fractional Differential Equations, 3rd edn, World Scientific, Singapore, 2023. -
-
-
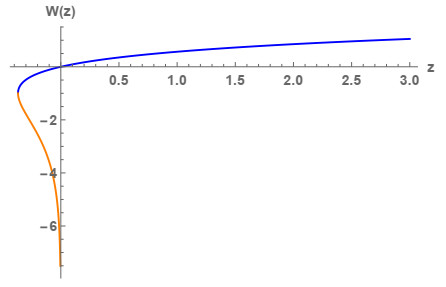
Figure 1.
Branches
$ \mathcal{W}_{-1} $ $ \mathcal{W}_0 $ $ w\mathrm{e}^w=z $ $ z=-\mathrm{e}^{-1}=-0.367879\ldots $ -
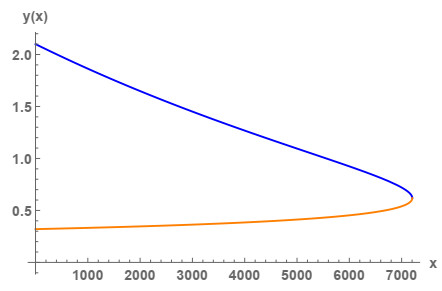
Figure 2.
Collapsing solutions of (4.1) for
$ \alpha=0.11 $ $ y_0=2.1 $ $ p=\pi $ -
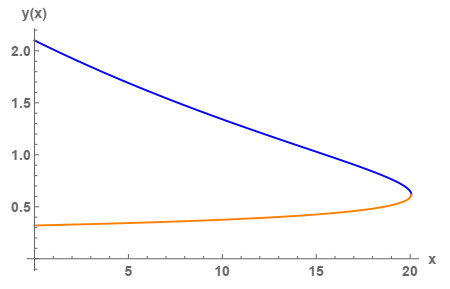
Figure 3.
Collapsing solutions of (4.1) for
$ \alpha=0.11 $ $ y_0=2.1 $ $ p=\pi $ -
Figure 4.
Ordinary solution of (4.1) for
$ \alpha=1 $ $ y_0=2.1 $ $ p=\pi $




 DownLoad:
DownLoad: