| Citation: |
Yanhua Zhu, You Li, Xiangyi Ma, Ying Sun, Ziwei Wang, Jinliang Wang. BIFURCATION AND TURING PATTERN ANALYSIS FOR A SPATIOTEMPORAL DISCRETE DEPLETION TYPE GIERER-MEINHARDT MODEL WITH SELF-DIFFUSION AND CROSS-DIFFUSION[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 705-733. doi: 10.11948/20240098
|
BIFURCATION AND TURING PATTERN ANALYSIS FOR A SPATIOTEMPORAL DISCRETE DEPLETION TYPE GIERER-MEINHARDT MODEL WITH SELF-DIFFUSION AND CROSS-DIFFUSION
-
Abstract
This paper presents a study on spatiotemporal dynamics and Turing patterns in a space-time discrete depletion type Gierer-Meinhardt model with self-diffusion and cross-diffusion based on coupled map lattices (CMLs) model. Initially, the existence and stability conditions for fixed points are determined through linear stability analysis. Secondly, the conditions for the occurrence of flip bifurcation, Neimark–Sacker bifurcation, and Turing bifurcation are derived by means of the center manifold reduction theorem and bifurcation theory. The results indicate that there exist two nonlinear mechanisms, namely flip-Turing instability and Neimark–Sacker-Turing instability. Additionally, some numerical simulations are performed to illustrate the theoretical findings. Interestingly, a rich variety of dynamical behaviors, including period-doubling cascades, invariant circles, periodic windows, chaotic regions, and striking pattern formations (plaques, mosaics, curls, spirals, and other intermediate patterns), are observed. Finally, the evolution of pattern size and type is also simulated as the cross-diffusion coefficient varies. It reveals that cross-diffusion has a certain influence on the growth of patterns.
-
-
References
[1] W. Abid, R. Yafia, M. A. Aziz-Alaoui, H. Bouhafa and A. Abichou, Diffusion driven instability and Hopf bifurcation in spatial predator-prey model on a circular domain, Applied Mathematics and Computation, 2015, 260, 292–313. doi: 10.1016/j.amc.2015.03.070 [2] L. Bai and G. Zhang, Nontrivial solutions for a nonlinear discrete elliptic equation with periodic boundary conditions, Applied Mathematics and Computation, 2009, 210(2), 321–333. doi: 10.1016/j.amc.2008.12.024 [3] M. Banerjee, Comments on "L. N. Guin, M. Haque and P. K. Mandal, The spatial patterns through diffusion-driven instability in a predator-prey model, Applied Mathematical Modelling, 2012, 36, 1825-1841. ", Applied Mathematical Modelling, 2015, 39(1), 297–299. doi: 10.1016/j.apm.2014.04.058 [4] M. Bendahmane, R. Ruiz-Baier and C. Tian, Turing pattern dynamics and adaptive discretization for a super-diffusive Lotka-Volterra model, Journal of Mathematical Biology, 2016, 72(6), 1441–1465. doi: 10.1007/s00285-015-0917-9 [5] J. Buceta and K. Lindenberg, Switching-induced Turing instability, Physical Review E, 2002, 66(4), 046202. doi: 10.1103/PhysRevE.66.046202 [6] Y. Cai, C. Zhao and W. Wang, Spatiotemporal complexity of a Leslie-Gower predator-prey model with the weak Allee effect, Journal of Applied Mathematics, 2013. DOI: 10.1155/2013/535746. [7] C. Castellano, S. Fortunato and V. Loreto, Statistical physics of social dynamics, Reviews of Modern Physics, 2007, 81(2), 591–646. [8] C. Castellano, H. Zhang and L. Dai, Regular and irregular vegetation pattern formation in semiarid regions: A study on discrete klausmeier model, Complexity, 2020, 2020, 2498073. [9] L. Chang, G. Sun, Z. Wang and Z. Jin, Rich dynamics in a spatial predator-prey model with delay, Applied Mathematics and Computation, 2015, 256, 540–550. doi: 10.1016/j.amc.2015.01.052 [10] M. Chen and Q. Zheng, Predator-taxis creates spatial pattern of a predator-prey model, Chaos Solitons & Fractals, 2022, 161, 112332. [11] G. Domokos and I. Scheuring, Discrete and continuous state population models in a noisy world, Journal of Theoretical Biology, 2004, 227(4), 535–545. doi: 10.1016/j.jtbi.2003.08.017 [12] S. Getzin, T. E. Erickson, H. Yizhaq, M. Muñoz-Rojas, A. Huth and K. Wiegand, Bridging ecology and physics: Australian fairy circles regenerate following model assumptions on ecohydrological feedbacks, Journal of Ecology, 2021, 109(1), 399–416. doi: 10.1111/1365-2745.13493 [13] A. Gierer and H. Meinhardt, Stripe and spot patterns in a gierer-meinhardt activator-inhibitor model with different sources, Kybernetik, 1972, 12(1), 30–39. doi: 10.1007/BF00289234 [14] L. Gu, P. Gong and H. Wang, Bifurcation and Turing instability analysis for the Gierer-Meinhardt model of the depletion type, Discrete Dynamics in Nature and Society, 2020, 2020, 5293748. [15] J. Guckenheimer and P. Holms, Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Springer, New York, 1983. [16] O. Hammer and H. Bucher, Reaction-diffusion processes: Application to the morphogenesis of ammonoid ornamentation, Physical Review E, 1999, 32(6), 841–852. [17] R. Han and B. Dai, Spatiotemporal pattern formation and selection induced by nonlinear cross-diffusion in a toxic-phytoplankton-zooplankton model with Allee effect, Nonlinear Analysis-Real World Applications, 2019, 45, 822–853. doi: 10.1016/j.nonrwa.2018.05.018 [18] R. Han, L. N. Guin and B. Dai, Cross-diffusion-driven pattern formation and selection in a modified Leslie-Gower predator-prey model with fear effect, Journal of Biological Systems, 2020, 28(1), 27–64. doi: 10.1142/S0218339020500023 [19] H. He, M. Xiao, J. He and W. Zheng, Regulating spatiotemporal dynamics for a delay Gierer-Meinhardt model, Physica A-Statistical Mechanics and its Applications, 2024, 637, 129603. doi: 10.1016/j.physa.2024.129603 [20] T. Huang and H. Zhang, Bifurcation, chaos and pattern formation in a space-and time-discrete predator-prey system, Chaos Solitons & Fractals, 2016, 91, 92–107. [21] T. Huang, H. Zhang and H. Yang, Spatiotemporal complexity of a discrete space-time predator-prey system with self- and cross-diffusion, Applied Mathematicak Modelling, 2017, 47, 637–655. doi: 10.1016/j.apm.2017.03.049 [22] Z. Jing and J. Yang, Bifurcation and chaos in discrete-time predator-prey system, Chaos Solitons & Fractals, 2006, 27(1), 259–277. [23] Y. Li, J. Wang and X. Hou, Stripe and spot patterns for the Gierer-Meinhardt model with saturated activator production, Journal of Mathematical Analysis and Applications, 2017, 449(2), 1863–1879. doi: 10.1016/j.jmaa.2017.01.019 [24] B. Liu, R. Wu and L. Chen, Turing-Hopf bifurcation analysis in a superdiffusive predator-prey model, Chaos, 2018, 28(11), 1–10. [25] B. Liu, R. Wu, N. Iqbal and L. Chen, Turing patterns in the Lengyel-Epstein system with superdiffusion, International Journal of Bifurcation and Chaos, 2017, 27(8), 1–17. [26] J. Liu, F. Yi and J. Wei, Multiple bifurcation analysis and spatiotemporal patterns in a 1-D Gierer-Meinhardt model of morphogenesis, International Journal of Bifurcation and Chaos, 2010, 20(4), 1007–1025. doi: 10.1142/S0218127410026289 [27] X. Liu and D. Xiao, Complex dynamic behaviors of a discrete-time predator-prey system, Chaos Solitons & Fractals, 2007, 32(1), 80–94. [28] F. Mai, L. Qin and G. Zhang, Turing instability for a semi-discrete Gierer-Meinhardt system, Physica A-Statistical Mechanics and Its Applications, 2012, 391(5), 2014–2022. doi: 10.1016/j.physa.2011.11.034 [29] H. Meinhardt and M. Klingler, A model for pattern formation on the shells of molluscs, Journal of Theoretical Biology, 1987, 126(1), 63–89. doi: 10.1016/S0022-5193(87)80101-7 [30] D. Mistro, L. Rodrigues and S. Petrovskii, Spatiotemporal complexity of biological invasion in a space- and time discrete predator-prey system with strong Allee effect, Ecological Complexity, 2012, 9, 16–32. doi: 10.1016/j.ecocom.2011.11.004 [31] A. Nayfeh and B. Balachandran, Applied Nonlinear Dynamics: Analytical, Computational, and Experimental Methods, Wiley, Weinheim, 1995. [32] K. M. Owolabi and A. Atangana, Numerical simulation of noninteger order system in subdiffusive, diffusive, and superdiffusive scenarios, Journal of Computational and Nonlinear Dynamics, 2017, 12(3), 031010. doi: 10.1115/1.4035195 [33] M. Perc and P. Grigolini, Collective behavior and evolutionary games-an introduction, Chaos Solitons & Fractals, 2013, 56, 1–5. [34] D. Punithan, D. K. Kim and R. I. McKay, Spatio-temporal dynamics and quantification of daisyworld in two dimensional coupled map lattices, Ecological Complexity, 2012, 12, 43–57. doi: 10.1016/j.ecocom.2012.09.004 [35] L. Rodrigues, D. Mistro and S. Petrovskii, Pattern formation in a space- and time-discrete predator-prey system with a strong allee effect, Theoretical Ecology, 2012, 5(3), 341–362. doi: 10.1007/s12080-011-0139-8 [36] S. Ruan, Diffusion–driven instability in the Gierer-Meinhardt model of morphogenesis, Natural Resource Modeling, 1998, 311(2), 131–141. [37] X. Tang and Y. Song, Cross-diffusion induced spatiotemporal patterns in a predator–prey model with herd behavior, Nonlinear Analysis-Real World Applications, 2015, 24, 36–49. doi: 10.1016/j.nonrwa.2014.12.006 [38] A. M. Turing, The chemical basis of morphogenesis, Bulletin of Mathematical Biology, 1952, 237, 37–72. [39] H. Wang and P. Liu, Pattern dynamics of a predator-prey system with cross-diffusion, Allee effect and generalized Holling Ⅳ functional response, Chaos Solitons & Fractals, 2023, 171, 113456. [40] J. Wang, X. Hou, Y. Li and Z. Jing, Stripe and spot patterns in a gierer-meinhardt activator-inhibitor model with different sources, International Journal of Bifurcation and Chaos, 2015, 25(8), 1550108. doi: 10.1142/S0218127415501084 [41] J. Wang, Y. Li, S. Zhong and X. Hou, Analysis of bifurcation, chaos and pattern formation in a discrete time and space Gierer Meinhardt system, Chaos Solitons & Fractals, 2019, 118, 1–17. [42] M. J. Ward and J. Wei, Hopf bifurcations and oscillatory instabilities of spike solutions for the one-dimensional Gierer-Meinhardt model, Journal of Ninlinear Science, 2003, 13(2), 209–264. [43] J. Wei and M. Winter, On the two-dimensional Gierer-Meinhardt system with strong coupling, SIAM Journal on Mathematical Analysis, 1999, 30(6), 1241–1263. doi: 10.1137/S0036141098347237 [44] R. Wu and L. Yang, Bogdanov-Takens bifurcation of codimension 3 in the Gierer-Meinhardt model, International Journal of Bifurcation and Chaos, 2023, 33(14), 2350163. doi: 10.1142/S0218127423501638 [45] R. Wu, Y. Zhou, Y. Shao and L. Chen, Bifurcation and Turing patterns of reaction-diffusion activator-inhibitor model, Physica A-Statistical Mechanics and Its Applications, 2017, 482, 597–610. doi: 10.1016/j.physa.2017.04.053 [46] R. Yang, Cross-diffusion induced spatiotemporal patterns in Schnakenberg reaction-diffusion model, Nonlinear Dynamical, 2020, 110(2), 1753–1766. [47] R. Yang and X. Yu, Turing-Hopf bifurcation in diffusive Gierer-Meinhardt model, International Journal of Bifurcation and Chaos, 2022, 32(05), 2250046. [48] F. Yi, J. Wei and J. Shi, Diffusion-driven instability and bifurcation in the Lengyel-Epstein system, Nonlinear Analysis-Real World Applications, 2008, 9(3), 1038–1051. doi: 10.1016/j.nonrwa.2007.02.005 [49] Q. Zheng, J. Shen, V. Pandey, L. Guan and Y. Guo, Turing instability in a network-organized epidemic model with delay, Chaos Solitons & Fractals, 2023, 168, 113205. [50] Q. Zheng, J. Shen, Y. Xu, V. Pandey and L. Guan, Pattern mechanism in stochastic SIR networks with ER connectivity, Physica A-Statistical Mechanics and its Applications, 2022, 603, 127765. doi: 10.1016/j.physa.2022.127765 [51] S. Zhong, J. Wang, J. Bao, Y. Li and N. Jiang, Spatiotemporal complexity analysis for a space-time discrete generalized toxic phytoplankton-zooplankton model with self-diffusion and cross-diffusion, International Journal of Bifurcation and Chaos, 2021, 31(1), 2150006. doi: 10.1142/S0218127421500061 [52] S. Zhong, J. Wang, Y. Li and N. Jiang, Bifurcation, chaos and Turing instability analysis for a space-time discrete Toxic Phytoplankton-Zooplankton model with self-diffusion, International Journal of Bifurcation and Chaos, 2021, 29(13), 1950184. -
-
Figures(13)
Export File
Citation
Yanhua Zhu, You Li, Xiangyi Ma, Ying Sun, Ziwei Wang, Jinliang Wang. BIFURCATION AND TURING PATTERN ANALYSIS FOR A SPATIOTEMPORAL DISCRETE DEPLETION TYPE GIERER-MEINHARDT MODEL WITH SELF-DIFFUSION AND CROSS-DIFFUSION[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 705-733. doi: 10.11948/20240098
Format
Content
DownLoad:
-
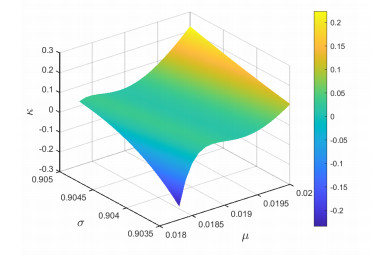
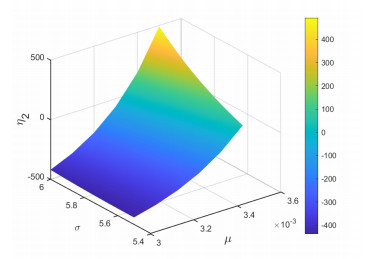
Figure 1.
The flip bifurcation surface in parameter space
$ (\mu, \sigma, \eta_2) $ -
Figure 2.
The Neimark-Sacker bifurcation surface in parameter space
$ (\mu, \sigma, \kappa) $ -
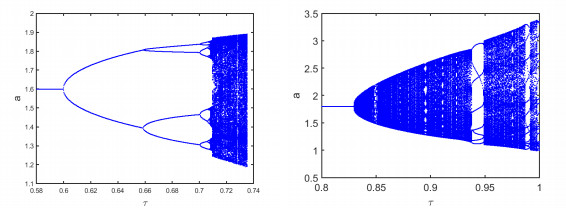
Figure 3.
(a) Flip bifurcation diagram; (b) Neimark-Sacker bifurcation diagram.
-
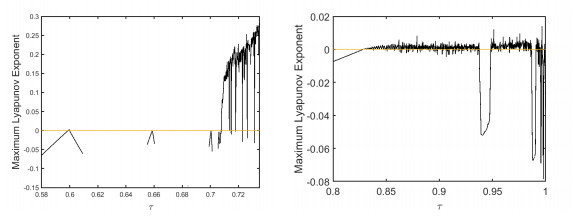
Figure 4.
(a) Maximum Lyapunov exponents of Flip bifurcation; (b) Maximum Lyapunov exponents of Neimark-Sacker bifurcation.
-
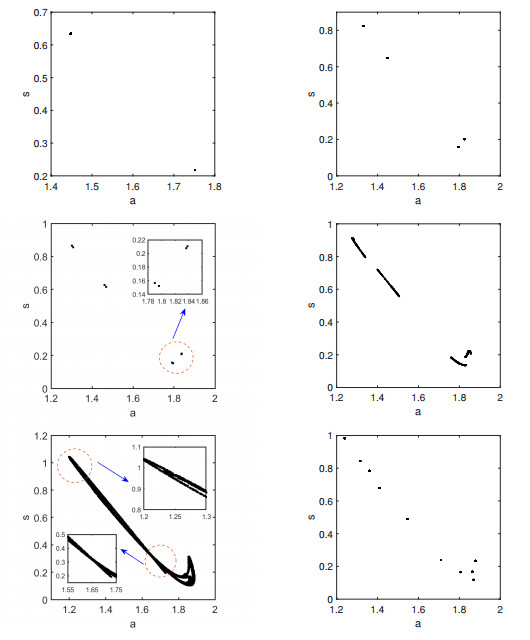
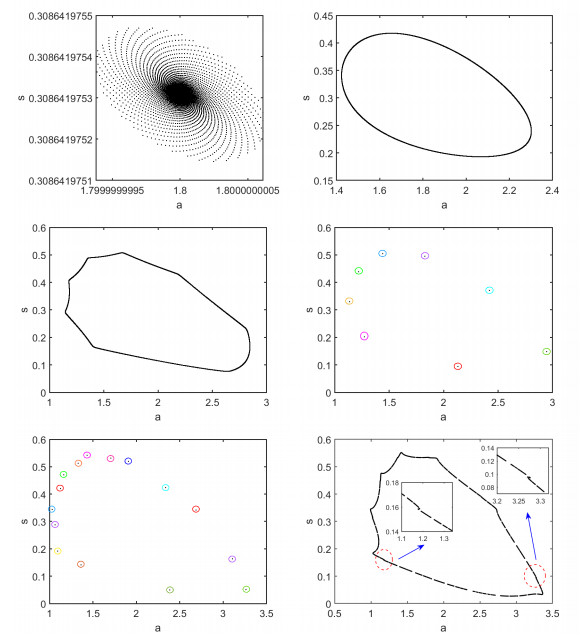
Figure 5.
Phase portraits for different values of
$ \tau $ $ \tau=0.63 $ $ \tau=0.68 $ $ \tau=0.7006 $ $ \tau=0.7093 $ $ \tau=0.73 $ $ \tau=0.736 $ -
Figure 6.
Phase portraits for different values of
$ \tau $ $ \tau=0.826 $ $ \tau=0.86 $ $ \tau=0.937 $ $ \tau=0.948 $ $ \tau=0.99 $ $ \tau=0.9962 $ -
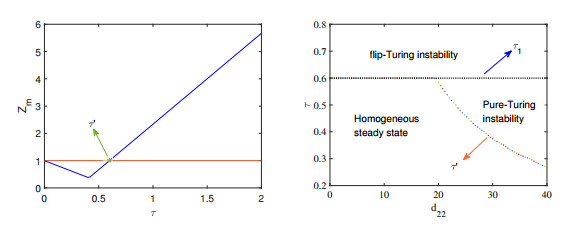
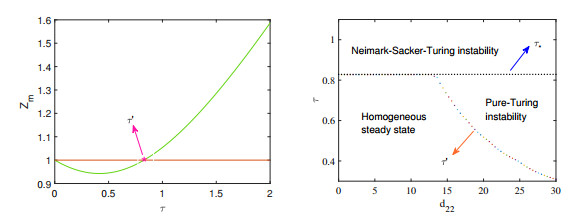
Figure 7.
(a)
$ Z_m-\tau $ $ \tau-d_{22} $ -
Figure 8.
(a)
$ Z_m-\tau $ $ \tau-d_{22} $ -
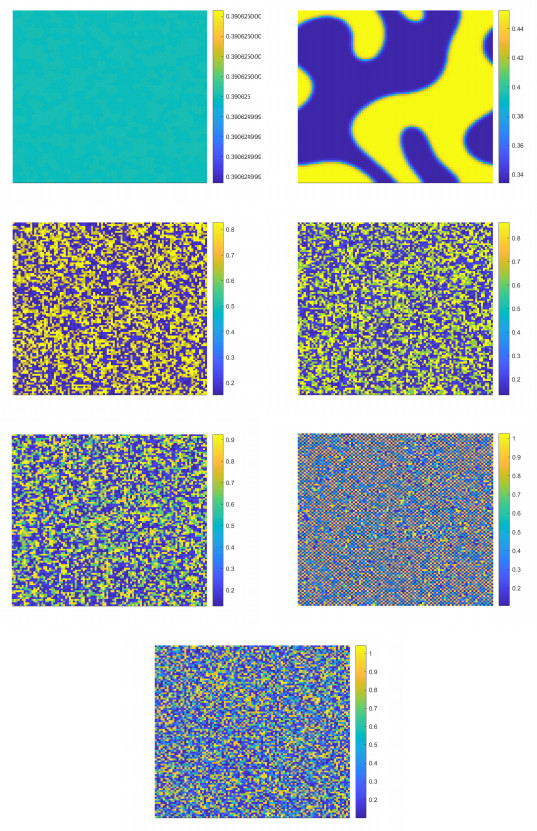
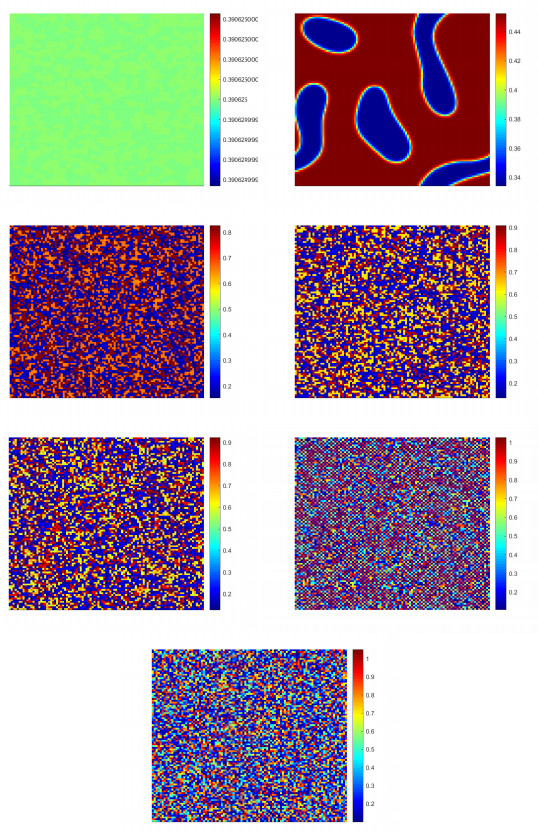
Figure 9.
Spatial patterns induced by flip-Turing instability with
$ d_{11}=0.5 $ $ d_{12}=0 $ $ d_{21}=0 $ $ d_{22}=0.6 $ $ \tau $ $ \tau=0.56 $ $ \tau=0.602 $ $ \tau=0.68 $ $ \tau=0.7006 $ $ \tau=0.7093 $ $ \tau=0.73 $ $ \tau=0.736 $ -
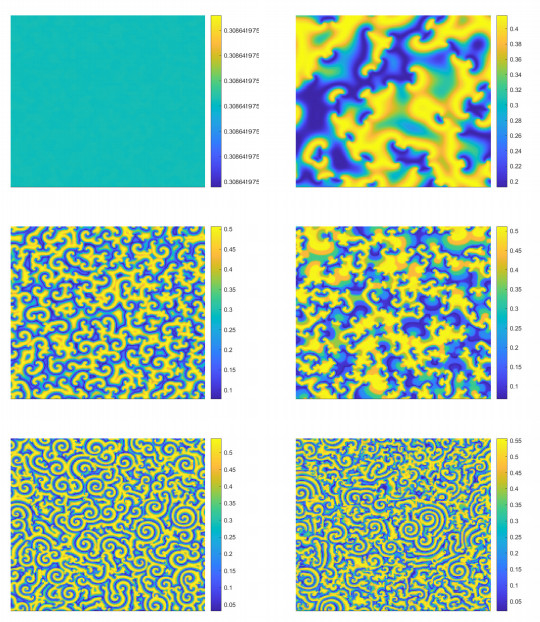
Figure 10.
Spatial patterns induced by flip-Turing instability with
$ d_{11}=0.5 $ $ d_{12}=0.05 $ $ d_{21}=0.06 $ $ d_{22}=0.6 $ $ \tau $ $ \tau=0.56 $ $ \tau=0.602 $ $ \tau=0.68 $ $ \tau=0.7006 $ $ \tau=0.7093 $ $ \tau=0.73 $ $ \tau=0.736 $ -
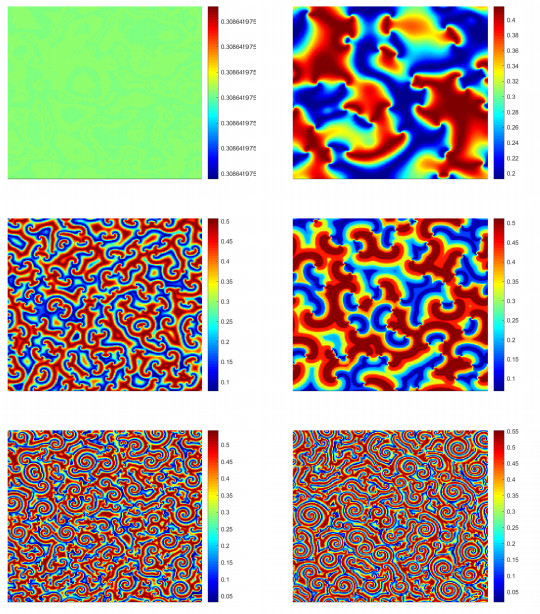
Figure 11.
Spatial patterns induced by Neimark-Sacker-Turing instability with
$ d_{11}=0.5 $ $ d_{12}=0 $ $ d_{21}=0 $ $ d_{22}=0.8 $ $ \tau $ $ \tau=0.826 $ $ \tau=0.86 $ $ \tau=0.937 $ $ \tau=0.948 $ $ \tau=0.99 $ $ \tau=0.9962 $ -
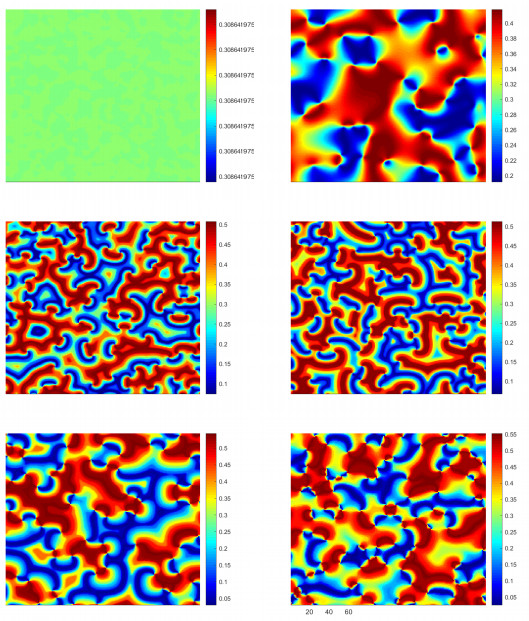
Figure 12.
Spatial patterns induced by Neimark-Sacker-Turing instability with
$ d_{11}=0.5 $ $ d_{12}=0.1 $ $ d_{21}=0.05 $ $ d_{22}=0.8 $ $ \tau $ $ \tau=0.826 $ $ \tau=0.86 $ $ \tau=0.937 $ $ \tau=0.948 $ $ \tau=0.99 $ $ \tau=0.9962 $ -
Figure 13.
Spatial patterns induced by Neimark-Sacker-Turing instability with
$ d_{11}=0.5 $ $ d_{12}=0.5 $ $ d_{21}=0.25 $ $ d_{22}=0.8 $ $ \tau $ $ \tau=0.826 $ $ \tau=0.86 $ $ \tau=0.937 $ $ \tau=0.948 $ $ \tau=0.99 $ $ \tau=0.9962 $