| Citation: |
Yong Yao, Jun He. BIFURCATIONS OF CODIMENSION THREE IN A LESLIE-GOWER TYPE PREDATOR-PREY SYSTEM WITH HERD BEHAVIOR AND PREDATOR HARVESTING[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 734-761. doi: 10.11948/20240107
|
BIFURCATIONS OF CODIMENSION THREE IN A LESLIE-GOWER TYPE PREDATOR-PREY SYSTEM WITH HERD BEHAVIOR AND PREDATOR HARVESTING
-
Abstract
A Leslie-Gower type predator-prey system with herd behavior in prey and constant harvesting in predators is considered in this paper. It is shown that there are two non-hyperbolic equilibria, one is a nilpotent cusp of codimension at most three and the other one is a weak focus of multiplicity also at most three. A complete analysis on bifurcations with codimension three is given as the bifurcation parameters vary, which includes a Bogdanov-Takens bifurcation of codimension three and a degenerate Hopf bifurcation of codimension three. The results indicate that the Leslie-Gower type system exhibits richer bifurcations than the classic Leslie-Gower model and also reveal the complexity of the interaction between the prey, predators and humans.
-
-
References
[1] V. Ajraldi, M. Pittavino and E. Venturino, Modeling herd behavior in population systems, Nonlinear Anal.-Real, 2011, 12(4), 2319–2338. doi: 10.1016/j.nonrwa.2011.02.002 [2] M. J. Álvarez, A. Ferragut and X. Jarque, A survey on the blow up technique, Int. J. Bifurcat. Chaos, 2011, 21(11), 3103–3118. doi: 10.1142/S0218127411030416 [3] P. A. Braza, Predator-prey dynamics with square root functional responses, Nonlinear Anal.-Real, 2012, 13(4), 1837–1843. doi: 10.1016/j.nonrwa.2011.12.014 [4] X. Chen and W. Zhang, Decomposition of algebraic sets and applications to weak centers of cubic systems, J. Comput. Appl. Math., 2009, 232(2), 565–581. doi: 10.1016/j.cam.2009.06.029 [5] S. N. Chow, C. Li and D. Wang, Normal Forms and Bifurcations of Plannar Vector Fields, Cambridge University Press, Cambridge, 1994. [6] F. Dumortier, R. Roussarie and J. Sotomayor, Generic 3-parameter families of vector fields on the plane, unfolding a singularity with nilpotent linear part, the cusp case of codimension 3, Ergod. Theor. Dyn. Syst., 1987, 7(3), 375–413. doi: 10.1017/S0143385700004119 [7] I. M. Gelfand, M. M. Kapranov and A. Zelevinsky, Discriminants, Resultants and Multidimensional Determinants, Birkhäuser, Boston, 1994. [8] E. González-Olivares, V. Rivera-Estay, A. Rojas-Palma and K. Vilches-Ponce, A leslie-gower type predator-prey model considering herd behavior, Ric. Mat., 2022, 1–24. [9] M. He and Z. Li, Global dynamics of a Leslie-Gower predator-prey model with square root response function, Appl. Math. Lett., 2023, 140, 108561. doi: 10.1016/j.aml.2022.108561 [10] S. B. Hsu and T. W. Hwang, Global stability for a class of predator-prey systems, SIAM J. Appl. Math., 1995, 55(3), 763–783. doi: 10.1137/S0036139993253201 [11] D. Hu, Y. Zhang, Z. Zheng and M. Liu, Dynamics of a delayed predator-prey model with constant-yield prey harvesting, J. Appl. Anal. Comput., 2022, 12(1), 302–335. [12] J. Huang, Y. Gong and S. Ruan, Bifurcation analysis in a predator-prey model with constant-yield predator harvesting, Discrete Cont. Dyn.-B, 2013, 18(8), 2101–2121. [13] J. Huang, S. Liu, S. Ruan and X. Zhang, Bogdanov-Tankens bifurcation of codimension 3 in a predator-prey model with constant-yield predator harvesting, Commun. Pur. Appl. Anal., 2016, 15(3), 1041–1055. doi: 10.3934/cpaa.2016.15.1041 [14] H. Jiang and X. Tang, Hopf bifurcation in a diffusive predator-prey model with herd behavior and prey harvesting, J. Appl. Anal. Comput., 2019, 9(2), 671–690. [15] A. Korobeinikov, A Lyapunov function for Leslie-Gower predator-prey models, Appl. Math. Lett., 2001, 14(6), 697–699. doi: 10.1016/S0893-9659(01)80029-X [16] Y. Lamontagne, C. Coutu and C. Rousseau, Bifurcation analysis of a predator-prey system with generalized Holling type III functional response, J. Dyn. Differ. Equ., 2008, 20(3), 535–571. doi: 10.1007/s10884-008-9102-9 [17] C. Li, J. Li and Z. Ma, Codimension 3 B-T bifurcation in an epidemic model with a nonlinear incidence, Discrete Cont. Dyn.-B, 2015, 20(4), 1107–1116. doi: 10.3934/dcdsb.2015.20.1107 [18] J. Luo and Y. Zhao, Stability and bifurcation analysis in a predator-prey system with constant harvesting and prey group defense, Int. J. Bifurcat. Chaos, 2017, 27(11), 1750179. doi: 10.1142/S0218127417501796 [19] M. G. Mortuja, M. K. Chaube and S. Kumar, Dynamic analysis of a predator-prey system with nonlinear prey harvesting and square root functional response, Chaos, Soliton. Fract., 2021, 148, 111071. doi: 10.1016/j.chaos.2021.111071 [20] M. G. Mortuja, M. K. Chaube and S. Kumar, Dynamic analysis of a modified Leslie-Gower model with nonlinear prey harvesting and prey herd behavior, Phys. Scripta, 2023, 98(12), 125216. doi: 10.1088/1402-4896/ad086b [21] S. Ruan and D. Xiao, Imperfect and BogdanovšCTakens bifurcations in biological models: from harvesting of species to isolation of infectives, J. Math. Biol., 2023, 87(1), 17. doi: 10.1007/s00285-023-01951-3 [22] Shivam, K. Singh, M. Kumar, R. Dubey and T. Singh, Untangling role of cooperative hunting among predators and herd behavior in prey with a dynamical systems approach, Chaos, Soliton. Fract., 2022, 162, 112420. doi: 10.1016/j.chaos.2022.112420 [23] F. Winkler, Polynomial Algorithms in Computer Algebra, Springer, New York, 1996. [24] C. Xiang, M. Lu and J. Huang, Degenerate Bogdanov-Takens bifurcation of codimension 4 in Holling-Tanner model with harvesting, J. Differ. Equations, 2022, 314, 370–417. doi: 10.1016/j.jde.2022.01.016 [25] D. Xiao and L. Jennings, Bifurcations of a ratio-dependent predator-prey system with constant rate harvesting, SIAM J. Appl. Math., 2005, 65(3), 737–753. doi: 10.1137/S0036139903428719 [26] D. Xiao, W. Li and M. Han, Dynamics in a ratio-dependent predator-prey model with predator harvesting, J. Math. Anal. Appl., 2006, 324(1), 14–29. doi: 10.1016/j.jmaa.2005.11.048 [27] Y. Xu, Y. Yang, F. Meng and S. Ruan, Degenerate codimension-2 cusp of limit cycles in a Holling-Tanner model with harvesting and anti-predator behavior, Nonlinear Anal.-Real, 2024, 76, 103995. doi: 10.1016/j.nonrwa.2023.103995 [28] L. Yang, Recent advances on determining the number of real roots of parametric polynomials, J. Symb. Comput., 1999, 28(1–2), 225–242. doi: 10.1006/jsco.1998.0274 [29] Z. Zhang, T. Ding, W. Huang and Z. Dong, Qualitative Theory of Differential Equations, American Mathematical Society, Providence, RI, 1992. -
-
Figures(4)
Export File
Citation
Yong Yao, Jun He. BIFURCATIONS OF CODIMENSION THREE IN A LESLIE-GOWER TYPE PREDATOR-PREY SYSTEM WITH HERD BEHAVIOR AND PREDATOR HARVESTING[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 734-761. doi: 10.11948/20240107
Format
Content
DownLoad:
-
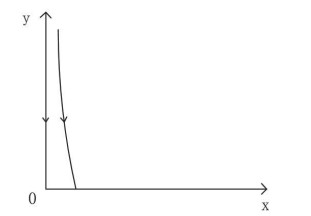
Figure 1.
The local phase portrait of system (1.5) near
$ (0, 0) $ $ \bar{\Omega} $ -
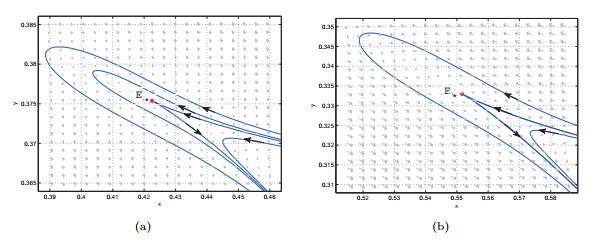
Figure 2.
The phase portraits of cusp
$ E_* $ $ s=0.1957 $ $ n=5.6131 $ $ h=0.0618 $ $ s=0.8056 $ $ n=2.0341 $ $ h=0.1887 $ -
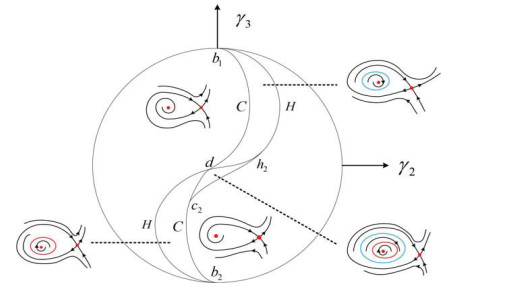
Figure 3.
Bifurcation diagram for system (1.4) on
$ S $ -
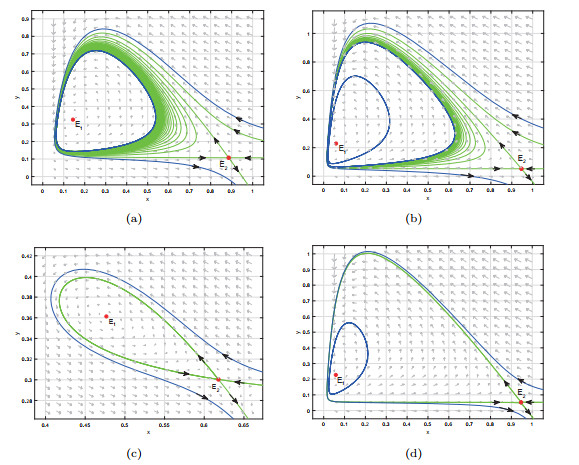
Figure 4.
Limit cycles and homoclinic orbit of system (1.4): (a) a stable limit cycle when
$ s=0.78 $ $ n=3.308 $ $ h=0.0807 $ $ s=0.78 $ $ n=4.995 $ $ h=0.0403 $ $ s=0.78 $ $ n=2.09799 $ $ h=0.18 $ $ s=0.78 $ $ n=5.0475 $ $ h=0.0403 $