| Citation: | Fanmeng Meng, Weihua Jiang, Xian-Feng Zhou, Song Liu. SOLVABILITY OF NONLOCAL HILFER FRACTIONAL MATRIX BOUNDARY VALUE PROBLEMS WITH $P$-LAPLACIAN AT RESONANCE IN $\mathbb{R}^N$[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 373-390. doi: 10.11948/20240112 |
SOLVABILITY OF NONLOCAL HILFER FRACTIONAL MATRIX BOUNDARY VALUE PROBLEMS WITH $P$-LAPLACIAN AT RESONANCE IN $\mathbb{R}^N$
-
Abstract
In this paper, the solvability of boundary value problems for a class of nonlinear Hilfer fractional differential equations at resonance in $ \mathbb{R}^n $ is studied. In the past, research on matrix boundary value problems has consistently been conducted within the context of linear differential equations. The main contribution of this paper is the extension of linear problems to nonlinear ones. We begin by defining two Banach spaces endowed with appropriate norms and constructing suitable operators in these Banach spaces. Subsequently, by using the extension for the continuous theorem, certain sufficient conditions for the solvability of the problem are obtained. Finally, an example is provided to verify the effectiveness of our main results.
-

-
References
[1] P. Aceves-Sanchez and L. Cesbron, Fractional diffusion limit for a fractional Vlasov-Fokker-Planck equation, SIAM J. Math. Anal., 2019, 51(1), 469–488. [2] M. Azouzi, L. Guedda and Z. Laadjal, Existence results of generalized proportional fractional differential equations at resonance case by the topological degree theory, Adv. Math., 2022, 11, 613–633. [3] Z. Baitiche, C. Derbazi and G. Wang, Monotone iterative method for nonlinear fractional $p$-Laplacian differential equation in terms of $\psi$-Caputo fractional derivative equipped with a new class of nonlinear boundary conditions, Math. Methods Appl. Sci., 2022, 45(2), 967–976. [4] A. Ben-Israel and T. N. E. Greville, Generalized Inverses: Theory and Applications, Springer-Verlag, New York, 2003. [5] N. Cao and X. Fu, Stationary distribution and extinction of a Lotka-Volterra model with distribute delay and nonlinear stochastic perturbations, Chaos Solitons Fractals, 2023, 169, 113246–113254. [6] R. Chaharpashlou and A. M. Lopes, Hyers-ulam-rassias stability of a nonlinear stochastic fractional volterra integro-differential equation, J. Appl. Anal. Comput., 2023, 13(5), 2799–2808. [7] W. Ding, J. P. Hollkamp, S. Patnaik, et al., On the fractional homogenization of one-dimensional elastic metamaterials with viscoelastic foundation, Advanced Structured Materials, 2023, 93(1), 261–286. [8] Y. Feng and Z. Bai, Solvability of some nonlocal fractional boundary value problems at resonance in $\mathbb{R}^n$, Fractal Fract., 2022, 6(1), 25–40. [9] M. M. Freitas, A. J. A. Ramos, A. Ö. Özer, et al., Long-time dynamics for a fractional piezoelectric system with magnetic effects and Fourier's law, J. Differential Equations, 2021, 280, 891–927. [10] W. Ge and J. Ren, An extension of Mawhin's continuation theorem and its application to boundary value problems with a p-Laplacain, Nonlinear Anal., 2004, 58(3–4), 477–488. [11] R. Hilfer, Applications of Fractional Calculus in Physics, World Scientific Publishing Co., Inc., River Edge, NJ, 2000. [12] W. Jiang, Solvability of fractional differential equations with $p$-Laplacian at resonance, Appl. Math. Comput., 2015, 260, 48–56. [13] B. Jin, Fractional Differential Equations–An Approach via Fractional Derivatives, Springer, Cham., 2021. [14] S. Khuri and R. Assadi, An extended variational iteration method for fractional BVPs encountered in engineering applications, Int. J. Numer. Method. H., 2023, 33(7), 2671–2681. [15] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and Applications of Fractional Differential Equations, Elsevier Science B. V., Amsterdam, 2006. [16] J. Kuang, Applied Inequalities, Shandong Science and Technology Press, Jinan, 2014. [17] T. A. M. Langlands, B. I. Henry and S. L. Wearne, Fractional cable equation models for anomalous electrodiffusion in nerve cells: Finite domain solutions, SIAM J. Appl. Math., 2011, 71(4), 1168–1203. [18] Z. Li, X. Huang and Y. Liu, Initial-boundary value problems for coupled systems of time-fractional diffusion equations, Fract. Calc. Appl. Anal., 2023, 26(2), 533–566. [19] P. Liu and H. Li, Global stability of autonomous and nonautonomous hepatitis B virus models in patchy environment, J. Appl. Anal. Comput., 2020, 10(5), 1771–1799. [20] J. Mawhin, Topological Degree Methods in Nonlinear Boundary Value Problems, American Mathematical Society, Providence, RI, 1979. [21] J. P. Ndenda, J. B. H. Njagarah and C. B. Tabi, Fractional-order model for myxomatosis transmission dynamics: Significance of contact, vector control and culling, SIAM J. Appl. Math., 2021, 81(2), 641–665. [22] G. Pang, L. Lu and G. E. Karniadakis, fPINNs: Fractional physics-informed neural networks, SIAM J. Sci. Comput., 2019, 41(4), A2603–A2626. [23] P. D. Phung and H. B. Minh, Existence of solutions to fractional boundary value problems at resonance in Hilbert spaces, Bound. Value Probl., 2017, 105, 1–20. [24] P. D. Phung and L. X. Truong, On the existence of a three point boundary value problem at resonance in $\mathbb{R}^n$, J. Math. Anal. Appl., 2014, 416(2), 522–533. [25] N. Raza, S. S. Kazmi and G. A. Basendwah, Dynamical analysis of solitonic, quasi-periodic, bifurcation and chaotic patterns of Landau-Ginzburg-higgs model, J. Appl. Anal. Comput., 2024, 14(1), 197–213. [26] A. Seal and S. Natesan, Convergence analysis of a second-order scheme for fractional differential equation with integral boundary conditions, J. Appl. Math. Comput., 2023, 69(1), 465–489. [27] Y. Wang, L. Liu and Y. Wu, Extremal solutions for $p$-Laplacian fractional integro-differential equation with integral conditions on infinite intervals via iterative computation, Adv. Difference Equ., 2015, 24, 1–14. [28] P. Wang, J. Wu, X. Xu, et al., Sharp decay estimates for Oldroyd-B model with only fractional stress tensor diffusion, J. Funct. Anal., 2022, 282(4), 109332–109387. [29] Y. Wang and H. Wang, Triple positive solutions for fractional differential equation boundary value problems at resonance, Appl. Math. Lett., 2020, 106, 376–382. [30] Q. Xu and J. S. Hesthaven, Discontinuous Galerkin method for fractional convection-diffusion equations, SIAM J. Numer. Anal., 2014, 52(1), 405–423. [31] M. A. Zaky, Existence, uniqueness and numerical analysis of solutions of tempered fractional boundary value problems, Appl. Numer. Math., 2019, 145, 429–457. -
-
-
Figure 1.
State
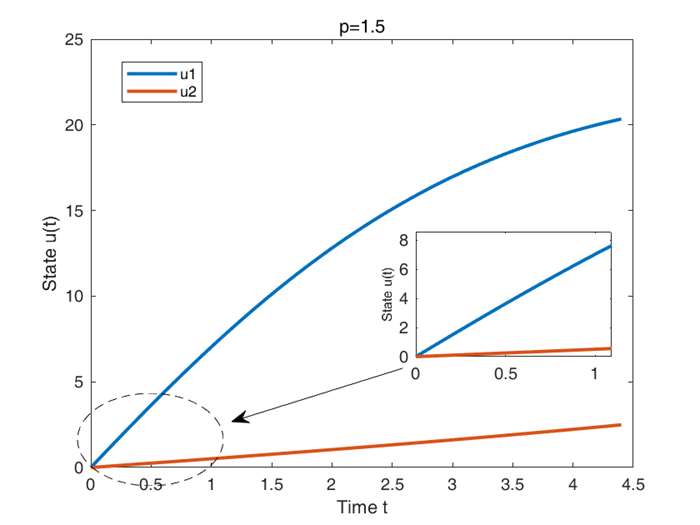
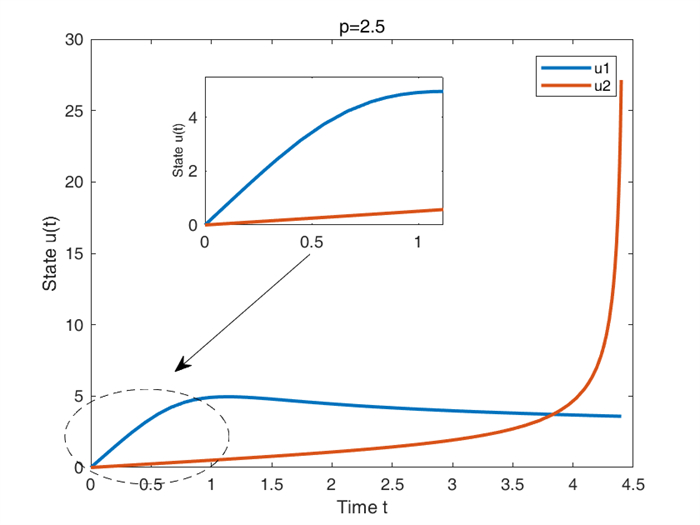
$ u(t) $ $ p=2.5 $ -
Figure 2.
State
$ u(t) $ $ p=1.5 $




 DownLoad:
DownLoad: