| Citation: | Jingping Lu, Chunyong Wang, Wentao Huang, Qinlong Wang. HOPF AND ZERO-HOPF BIFURCATIONS FOR A CLASS OF CUBIC KOLMOGOROV SYSTEMS IN $ \mathbb R^{3}$[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 354-372. doi: 10.11948/20240108 |
HOPF AND ZERO-HOPF BIFURCATIONS FOR A CLASS OF CUBIC KOLMOGOROV SYSTEMS IN $ \mathbb R^{3}$
-
Abstract
In this paper, Hopf and zero-Hopf bifurcations are investigated for a class of three-dimensional cubic Kolmogorov systems with one positive equilibrium. Firstly, by computing the singular point quantities and figuring out center conditions, we determined that the highest order of the positive equilibrium is eight as a fine focus, which yields Hopf cyclicity eight at the positive equilibrium. Secondly, by extending the normal form method, we discuss the existence of multiple periodic solutions via zero-Hopf bifurcation around the positive equilibrium. At the same time, the relevance between zero-Hopf bifurcation and Hopf bifurcation is analyzed via its special case, which are rarely studied in detail.
-

-
References
[1] A. Buicǎ, I. García and S. Maza, Multiple Hopf bifurcation in ${\mathbb R}^3$ and inverse Jacobi multipliers, J. Diff. Eqs., 2014, 256, 310–325. doi: 10.1016/j.jde.2013.09.006 CrossRef ${\mathbb R}^3$ and inverse Jacobi multipliers" target="_blank">Google Scholar
[2] M. Candido and J. Llibre, Zero-Hopf bifurcations in 3-dimensional differential systems with no equilibria, Math. Comput. Simulat., 2018, 151, 54–76. doi: 10.1016/j.matcom.2018.03.008 [3] J. Chavarriga, H. Giacomini, J. Giné and J. Llibre, Darboux integrability and the inverse integrating factor, J. Diff. Eqs., 2003, 194(1), 116–139. doi: 10.1016/S0022-0396(03)00190-6 [4] E. Diz-Pita, J. Llibre, M. Victoria Otero-Espinar and C. Valls, The zero-Hopf bifurcations in the Kolmogorov systems of degree 3 in $\mathbb R^3$, Commun. Nonlinear Sci. Numer. Simulat., 2021, 95, 105621. doi: 10.1016/j.cnsns.2020.105621 [5] C. Du and W. Huang, Center-focus problem and limit cycles bifurcations for a class of cubic Kolmogorov model, Nonlinear Dyn., 2013, 72, 197–206. doi: 10.1007/s11071-012-0703-9 [6] C. Du, Q. Wang and W. Huang, Three-dimensional Hopf bifurcation for a class of cubic Kolmogorov model, Int. J. Bifur. Chaos, 2014, 24, 1450036. doi: 10.1142/S0218127414500369 [7] V. Edneral, A. Mahdi, V. G. Romanovskic and D. Shafer, The center problem on a center manifold in ${\mathbb R}^3$, Nonlinear Anal. Real World Appl., 2012, 75, 2614–2622. [8] I. García, S. Maza and D. Shafer, Cyclicity of polynomial nondegenerate centers on center manifolds, J. Diff. Eqs., 2018, 265, 5767–5808. doi: 10.1016/j.jde.2018.07.019 [9] J. Gu, A. Zegeling and W. Huang, Bifurcation of limit cycles and isochronous centers on center manifolds for a class of cubic Kolmogorov systems in $R^{3}$, Qual. Theory Dyn. Syst., 2023, 22, 42. doi: 10.1007/s12346-023-00745-8 [10] M. Han and P. Yu, Normal Forms, Melnikov Functions and Bifurcations of Limit Cycles, New York, Springer, 2012. [11] B. Hassard, N. Kazarinoff and Y. Wan, Theory and Application of Hopf Bifurcation, Cambridge, Cambridge University Press, 1981. [12] D. He, W. Huang and Q. Wang, Small amplitude limit cycles and local bifurcation of critical periods for a quartic Kolmogorov system, Qual. Theory Dyn. Syst., 2020, 19, 68. doi: 10.1007/s12346-020-00401-5 [13] M. Hirsch, Systems of differential equations that are competitive or cooperative, V: Convergence in 3-dimensional systems, J. Diff. Eqs., 1989, 80, 94–106. doi: 10.1016/0022-0396(89)90097-1 [14] W. Huang, Q. Wang and A. Chen, Hopf bifurcation and the centers on center manifold for a class of three-dimensional circuit system, Math. Methods Appl. Sci., 2020, 43(4), 1988–2000. doi: 10.1002/mma.6026 [15] A. Kolmogorov, Sulla teoria di volterra della lotta per l'esistenza, Gi. Inst. Ital. Attuari, 1936, 7, 74–80. [16] F. Li, Y. Liu, Y. Liu and P. Yu, Complex isochronous centers and linearization transformations for cubic $Z_2$ equivariant planar systems, J. Diff. Eqs., 2020, 268, 3819–3847. doi: 10.1016/j.jde.2019.10.011 CrossRef $Z_2$ equivariant planar systems" target="_blank">Google Scholar
[17] Y. Liu and J. Li, Theory of values of singular point in complex autonomous differential system, Sci. China Ser. A, 1990, 33, 10–24. [18] J. Llibre and K. Ammar, Zero-Hopf periodic orbits for a Rössler differential system, Int. J. Bifur. Chaos, 2020, 12, 2050170. [19] N. Lloyd, J. Pearson, E. Sáez and I. Szántó, Limit cycles of a cubic Kolmogorov system, Appl. Math. Lett., 1996, 9, 15–18. [20] J. Lu, C. Wang, W. Huang and Q. Wang, Local bifurcation and center problem for a more generalized Lorenz system, Qual. Theory Dyn. Syst., 2022, 21(4), 96. doi: 10.1007/s12346-022-00629-3 [21] D. Rodrigo and J. Llibre, Zero-Hopf bifurcation in a Chua system, Nonlinear Anal. Real World Appl., 2017, 37, 31–40. doi: 10.1016/j.nonrwa.2017.02.002 [22] V. G. Romanovski, Y. Xia and X. Zhang, Varieties of local integrability of analytic differential systems and their applications, J. Diff. Eqs., 2014, 257, 3079–3101. doi: 10.1016/j.jde.2014.06.007 [23] Y. Tian and P. Yu, An explicit recursive formula for computing the normal form and center manifold of n-dimensional differential systems associated with Hopf bifurcation, Int. J. Bifur. Chaos, 2013, 23, 1350104. doi: 10.1142/S0218127413501046 [24] Y. Tian and P. Yu, An explicit recursive formula for computing the normal forms associated with semisimple cases, Commun. Nonlinear Sci., 2014, 19(7), 2294–2308. doi: 10.1016/j.cnsns.2013.11.019 [25] Q. Wang, W. Huang and J. Feng, Multiple limit cycles and centers on center manifolds for Lorenz system, Appl. Math. Comput., 2014, 238, 281–288. [26] Q. Wang, W. Huang and B. Li, Limit cycles and singular point quantities for a 3D Lotka-Volterra system, Appl. Math. Comput., 2011, 217, 8856–8859. [27] Q. Wang, Y. Liu and H. Chen, Hopf bifurcation for a class of three-dimensional nonlinear dynamic systems, Bull. Sci. Math., 2010, 134, 786–798. doi: 10.1016/j.bulsci.2009.12.001 [28] Y. Ye and W. Ye, Cubic Kolmogorov systems with two limit cycles surrounding the same focus, Ann. Differ. Equ., 1985, 1, 201–207. [29] P. Yu, Computation of normal forms via a perturbation technique, J. Sound Vib., 1998, 211(1), 19–38. doi: 10.1006/jsvi.1997.1347 [30] P. Yu, M. Han and D. Xiao, Four small limit cycles around a Hopf singular point in 3-dimensional competitive Lotka-Volterra systems, J. Math. Anal. Appl., 2016, 436(1), 521–555. doi: 10.1016/j.jmaa.2015.12.002 [31] P. Yu and Y. Yuan, The simplest normal form for the singularity of a pure imaginary pair and a zero eigenvalue, Dyn. Cont. Discr. Impuls. Syst. Ser. B, 2001, 8, 219–249. [32] B. Zeng and P. Yu, Analysis of zero-Hopf bifurcation in two Rössler systems using normal form theory, Int. J. Bifur. Chaos, 2020, 16, 2030050. -
-
-
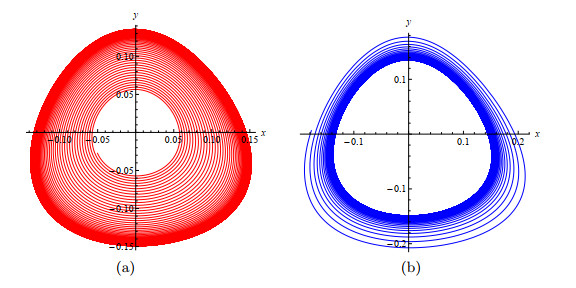
Figure 1.
Projection of phase portraits on the plane
$ x $ $ y $ $ \lambda=-1.5, \delta=0.02 $ $ A_{200}=-2 $ $ (x_0, y_0, u_0) = (0.05, 0, 0.05) $ $ (x_0, y_0, u_0) =(0.2, 0, 0.15) $ -
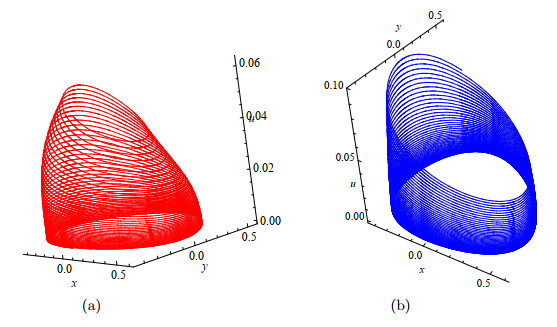
Figure 2.
Simulations of system (4.8) for
$ \lambda=-0.01, \delta=0.02, A_{200}=-0.3 $ $ (x_0, y_0, u_0) = (0.05, 0, 0.08) $ $ (x_0, y_0, u_0) =(0.5, 0, 0.05) $ -
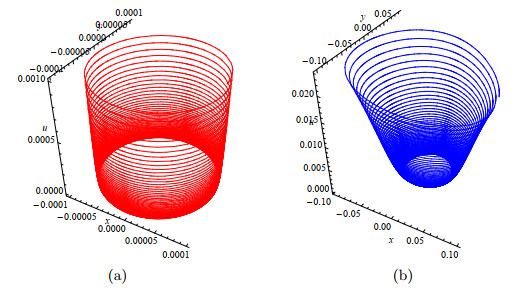
Figure 3.
Simulations of system (4.8) with
$ \lambda=-0.01, \delta=0 $ $ A_{200}=-3 $ $ (x_0, y_0, u_0) = (0.0001, 0, 0.001) $ $ (x_0, y_0, u_0) =(0.1, 0, 0.02) $




 DownLoad:
DownLoad: