| Citation: |
Parisa Rahimkhani, Salameh Sedaghat. ALTERNATIVE WAVELETS FOR THE SOLUTION OF VARIABLE-ORDER FRACTAL-FRACTIONAL DIFFERENTIAL EQUATIONS SYSTEM WITH POWER AND MITTAG-LEFFLER KERNELS[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 1830-1861. doi: 10.11948/20240117
|
ALTERNATIVE WAVELETS FOR THE SOLUTION OF VARIABLE-ORDER FRACTAL-FRACTIONAL DIFFERENTIAL EQUATIONS SYSTEM WITH POWER AND MITTAG-LEFFLER KERNELS
-
Abstract
In this paper, a procedure based on the fractional-order alternative Legendre wavelets (FALWs) is introduced for solving variable-order fractalfractional differential equations (VFFDEs) system with power and MittagLeffler kernels. An analytic formula is obtained for computing the variableorder fractal-fractional integral operator of the FALWs by employing the regularized beta functions. The presented method converts solving the primary problem to solving a system of nonlinear algebraic equations. To do this, the variable-order fractal-fractional (VFF) derivative of the unknown function is expanded in terms of the FALWs with unknown coefficients at first. Then, by employing the properties of the VFF derivative and integral, together with the collocation method, a system of algebraic equations is obtained, that can be easily solved by the Newton's iterative scheme. An error upper bound for the numerical solution in the Sobolev space is obtained. Finally, different chaotic oscillators of variable-order are solved in order to illustrate the accuracy and validity of the suggested strategy.
-
-
References
[1] R. Almeida, A. B. Malinowska and M. T. T. Monteiro, Fractional differential equations with a Caputo derivative with respect to a kernel function and their applications, Math. Method. Appl. Sci., 2018, 41, 336–352. doi: 10.1002/mma.4617 [2] M. Alqhtani and K. M. Saad, Fractal-fractional Michaelis-Menten enzymatic reaction model via different kernels, Fractal and Fractional, 2022, 6, 13. [3] A. Atangana, Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system, Chaos Solitons and Fractals, 2017, 102, 396–406. doi: 10.1016/j.chaos.2017.04.027 [4] A. Atangana and S. Qureshi, Modeling attractors of chaotic dynamical systems with fractal-fractional operators, Chaos Solitons and Fractals, 2019, 123, 320–337. doi: 10.1016/j.chaos.2019.04.020 [5] R. L. Bagley and P. J. Torvik, Fractional calculus in the transient analysis of viscoelastically damped structures, AIAA J., 1985, 23, 918–925. doi: 10.2514/3.9007 [6] Q. H. Do, H. T. B. Ngo and M. Razzaghi, A generalized fractional-order Chebyshev wavelet method for two-dimensional distributed-order fractional differential equations, Communications in Nonlinear Science and Numerical Simulation, 2021, 95, 105597. doi: 10.1016/j.cnsns.2020.105597 [7] N. Engheta, On fractional calculus and fractional multipoles in electromagnetism, Antennas Propag., 1996, 44, 554–566. doi: 10.1109/8.489308 [8] M. H. Heydari, Numerical solution of nonlinear 2D optimal control problems generated by Atangana-Riemann-Liouville fractal-fractional derivative, Applied Numerical Mathematics, 2020, 150, 507–518. doi: 10.1016/j.apnum.2019.10.020 [9] M. H. Heydari, A. Atangana and Z. Avazzadeh, Numerical solution of nonlinear fractal-fractional optimal control problems by Legendre polynomials, Math. Methods Appl. Sci., 2021, 44(4), 2952–2963. doi: 10.1002/mma.6326 [10] M. H. Heydari, A. Atangana, Z. Avazzadeh and Y. Yang, Numerical treatment of the strongly coupled nonlinear fractal-fractional Schr$\ddot{o}$dinger equations through the shifted Chebyshev cardinal functions, Math. Meth. Appl. Sci., 2020, 59(4), 2037–2052. [11] M. H. Heydari, Z. Avazzadeh and A. Atangana, Shifted Vieta-Fibonacci polynomials for the fractal-fractional fifth-order KdV equation, Math. Meth. Appl. Sci., 2021, 44, 6716–6730. doi: 10.1002/mma.7219 [12] E. Keshavarz, Y. Ordokhani and M. Razzaghi, The Taylor wavelets method for solving the initial and boundary value problems of Bratu-type equations, Appl. Numer. Math., 2018, 128, 205–216. doi: 10.1016/j.apnum.2018.02.001 [13] V. V. Kulish and J. L. Lage, Application of fractional calculus to fluid mechanics, J. Fluids Eng., 2002, 124(3), 803–806. doi: 10.1115/1.1478062 [14] C. Lederman, J. M. Roquejoffre and N. Wolanski, Mathematical justification of a nonlinear integro–differential equation for the propagation of spherical flames, Annali di Matematica, 2004, 183, 173–239. doi: 10.1007/s10231-003-0085-1 [15] F. C. Meral, T. J. Royston and R. Magin, Fractional calculus in viscoelasticity: An experimental study, Commun. Nonlinear Sci. Numer. Simul., 2010, 15, 939–945. doi: 10.1016/j.cnsns.2009.05.004 [16] S. Nemati, P. M. Lima and S. Sedaghat, Legendre wavelet collocation method combined with the Gauss-Jacobi quadrature for solving fractional delay-type integro-differential equations, Appl. Numer. Math., 2020, 149, 99–112. doi: 10.1016/j.apnum.2019.05.024 [17] N. T. B. Ngo, T. N. Vo and M. Razzaghi, An effective method for solving nonlinear fractional differential equations, Engineering with Computers, 2022, 38, 207–218. doi: 10.1007/s00366-020-01143-3 [18] K. M. Owolabi, A. Atangana A and A. Akgul, Modelling and analysis of fractal-fractional partial differential equations: Application to reaction-diffusion model, Alex. Eng. J., 2020, 1, 1–17. [19] I. Podlubny, Fractional Differential Equations, Academic Press, San Diego, 1999. [20] P. Rahimkhani, Numerical solution of nonlinear stochastic differential equations with fractional Brownian motion using fractional-order Genocchi deep neural networks, Communications in Nonlinear Science and Numerical Simulation, 2023, 126, 107466. doi: 10.1016/j.cnsns.2023.107466 [21] P. Rahimkhani and M. H. Heydari, Fractional shifted Morgan-Voyce neural networks for solving fractal-fractional pantograph differential equations, Chaos, Solitons and Fractals, 2023, 175, 114070. doi: 10.1016/j.chaos.2023.114070 [22] P. Rahimkhani and Y. Ordokhani, The bivariate Muntz wavelets composite collocation method for solving space-time fractional partial differential equations, Comput. Appl. Math., 2020, 39, 115. doi: 10.1007/s40314-020-01141-7 [23] P. Rahimkhani and Y. Ordokhani, Hahn wavelets collocation method combined with Laplace transform method for solving fractional integro-differential equations, Mathematical Sciences, 2023. DOI: 10.1007/s40096-023-00514-3. [24] P. Rahimkhani and Y. Ordokhani, Numerical investigation of distributed-order fractional optimal control problems via Bernstein wavelets, Opt. Control Appl. Methods., 2021, 42(1), 355–373. doi: 10.1002/oca.2679 [25] P. Rahimkhani and Y. Ordokhani, Approximate solution of nonlinear fractional integro-differential equations using fractional alternative Legendre functions, Journal of Computational and Applied Mathematics, 2020, 365, 112365. doi: 10.1016/j.cam.2019.112365 [26] P. Rahimkhani and Y. Ordokhani, A modified numerical method based on Bernstein wavelets for numerical assessment of fractional variational and optimal control problems, Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 2022. DOI: 10.1007/s40998-022-00522-4. [27] P. Rahimkhani, Y. Ordokhani and P. M. Lima, An improved composite collocation method for distributed-order fractional differential equations based on fractional Chelyshkov wavelets, Appl. Numer. Math., 2019, 145, 1–27. doi: 10.1016/j.apnum.2019.05.023 [28] P. Rahimkhani, Y. Ordokhani and S. Sabermahani, Bernoulli wavelet least square support vector regression: Robust numerical method for a system of fractional differential equations, Mathematical Methods in the Applied Sciences, 2023. DOI: 10.1002/mma.9522. [29] P. Rahimkhani, Y. Ordokhani and S. Sedaghat, The numerical treatment of fractal-fractional 2D optimal control problems by Mü ntz-Legendre polynomials, Optimal Control, Applications and Methods, 2023. DOI: 10.1002/oca.3024. [30] S. Sabermahani, Y. Ordokhani and P. Rahimkhani, Touchard-Ritz method to solve variable-order fractional optimal control problems, Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 2024, 48, 1189–1198. doi: 10.1007/s40998-024-00735-9 [31] S. Sabermahani, Y. Ordokhani and P. Rahimkhani, Application of generalized Lucas wavelet method for solving nonlinear fractal-fractional optimal control problems, Chaos Solitons Fractals, 2023, 170, 113348. doi: 10.1016/j.chaos.2023.113348 [32] S. Sabermahani, Y. Ordokhani and S. A. Yousefi, Fractional-order general Lagrange scaling functions and their applications, BIT Numer. Math., 2019, 60, 101–128. doi: 10.1007/s10543-019-00769-0 [33] S. Sedaghat and S. Mashayekhi, Exploiting delay differential equations solved by Eta functions as suitable mathematical tools for the investigation of thickness controlling in rolling mill, Chaos, Solitons and Fractals, 2022, 164, 112666. doi: 10.1016/j.chaos.2022.112666 [34] J. E. Solis–Perez and J. F. Gomez–Aguilar, Variable order fractal–fractional time delay equations with power, exponential and Mittag–Leffler laws and their numerical solutions, Engineering with Computers, 2022, 38, 555–577. doi: 10.1007/s00366-020-01065-0 [35] H. M. Srivastava and K. M. Saad, Numerical simulation of the fractal-fractional Ebola virus, Fractal Fract., 2020, 4(4), 49. doi: 10.3390/fractalfract4040049 [36] M. H. Srivastava, K. M. Saad and W. M. Hamanah, Certain new models of the multi-space fractal-fractional Kuramoto-Sivashinsky and Korteweg-de Vries equations, Mathematics, Mathematics, 2022, 10(7), 1089. [37] P. T. Toan, T. N. Vo and M. Razzaghi, Taylor wavelet method for fractional delay differential equations, Eng. Comput., 2019, 1–10. [38] W. Wang and M. A. Khan, Analysis and numerical simulation of fractional model of bank data with fractal-fractional Atangana-Baleanu derivative, Journal of Computational and Applied Mathematics, 2020, 369, 112646. [39] C. J. Zuniga–Aguilar, J. F. Gomez–Aguilar, H. M. Romero–Ugalde, R. F. Escobar–Jimenez, G. FernndezAnaya and F. E. Alsaadi, Numerical solution of fractal-fractional Mittag–Leffler differential equations with variable-order using artificial neural networks, Engineering with Computers, 2022, 38, 2669–2682. -
-
Figures(12) / Tables(10)
Export File
Citation
Parisa Rahimkhani, Salameh Sedaghat. ALTERNATIVE WAVELETS FOR THE SOLUTION OF VARIABLE-ORDER FRACTAL-FRACTIONAL DIFFERENTIAL EQUATIONS SYSTEM WITH POWER AND MITTAG-LEFFLER KERNELS[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 1830-1861. doi: 10.11948/20240117
Format
Content
DownLoad:
-
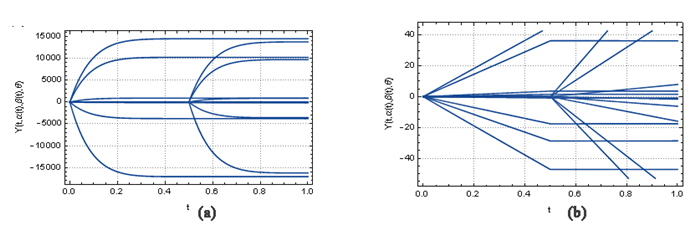
Figure 1.
The graphs of the fractional-order alternative wavelets with
$ \theta , t \in [0, 1] $ $ (k=2, M=10) $ $ (k=3, M=8) $ -
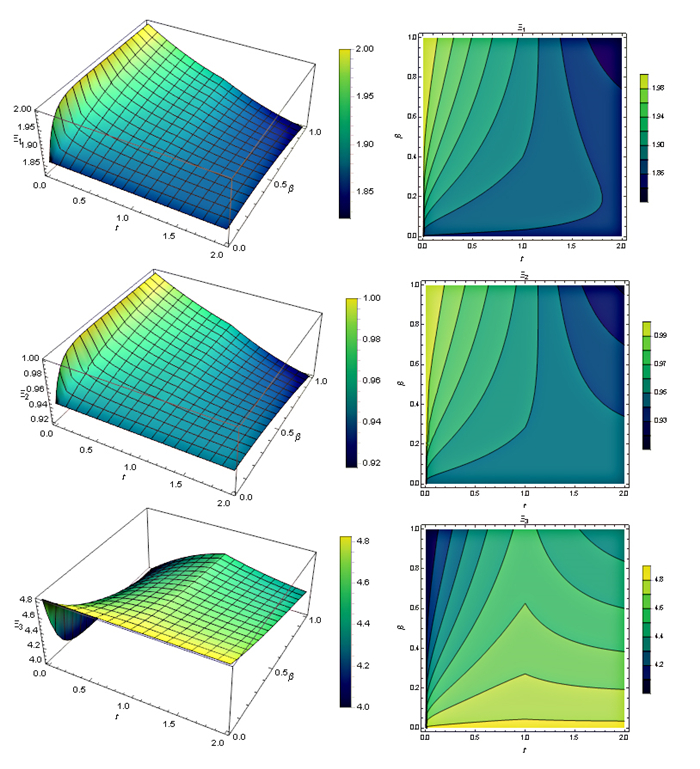
Figure 2.
The graphs of the CFF variable-order integral with
$ k=2, M=8, h=1, \alpha (t)= \tanh (t+5), \beta (t)=0.99+\frac{0.01}{2}(\sin (t)+1) $ $ (a): \theta =1 $ $ (b): \theta = \frac{1}{8} $ -
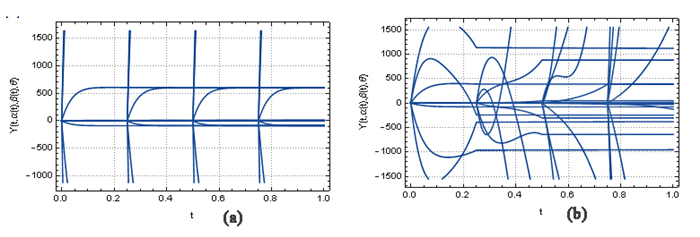
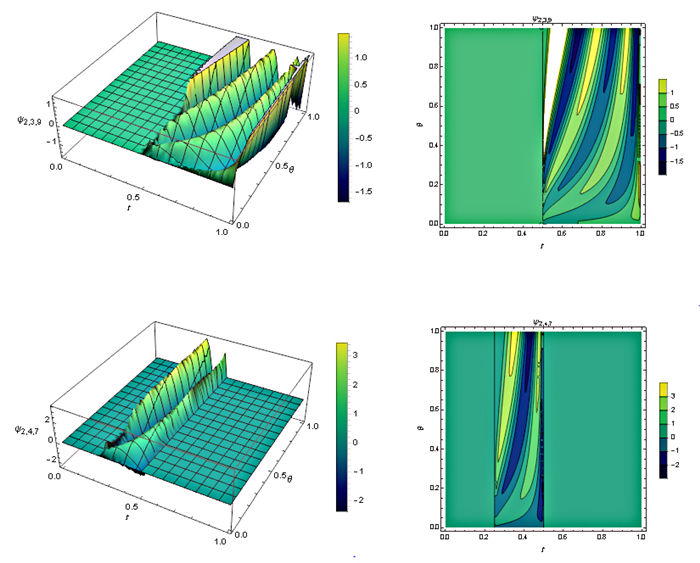
Figure 3.
The graphs of the CFF variable-order integral with
$ k=3, M=8, h=1, \alpha (t)= \tanh (t+5), \beta (t)=0.99+\frac{0.01}{2}(\sin (t)+1) $ $ (a): \theta =1 $ $ (b): \theta = \frac{2}{3} $ -
Figure 4.
The NR with
$ k=2, M=6, h=2, \theta =\frac{1}{4} $ $ \beta (t) \in (0, 1) $ -
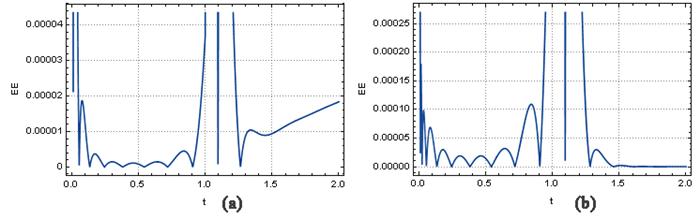
Figure 5.
The EE with
$ k=2, M=8, h=2, \theta =\frac{1}{8} $ $ (a): $ $ (b): $ -
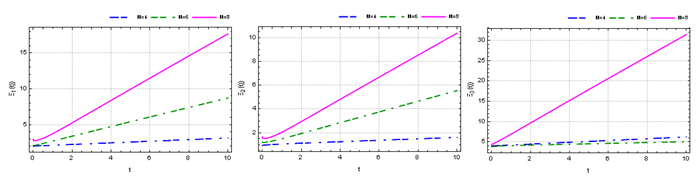
Figure 6.
The NR with
$ k=1, h=10, \theta =\frac{1}{8} $ $ M=4, 6, 8 $ -
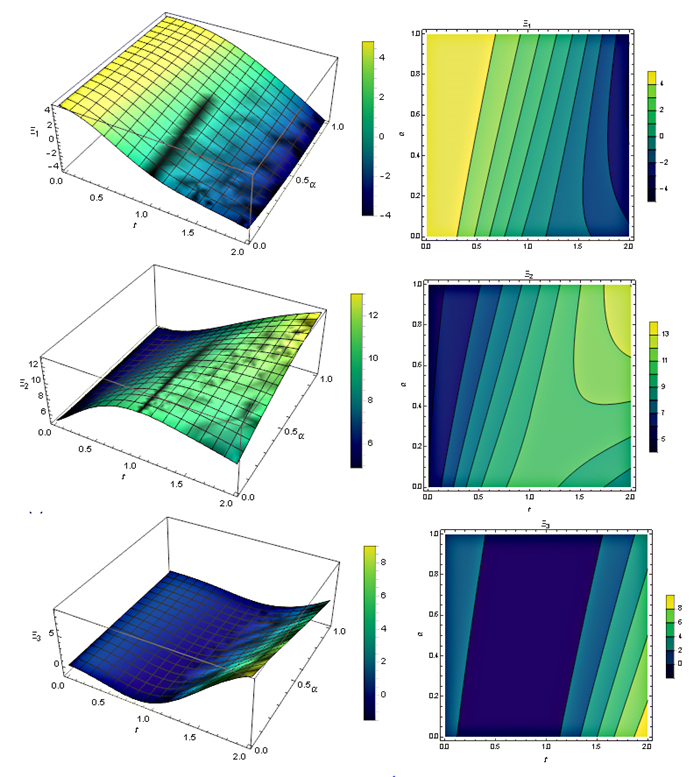
Figure 7.
The NR with
$ k=2, M=9, h=2, \theta =1 $ $ \alpha (t) \in (0, 1) $ -
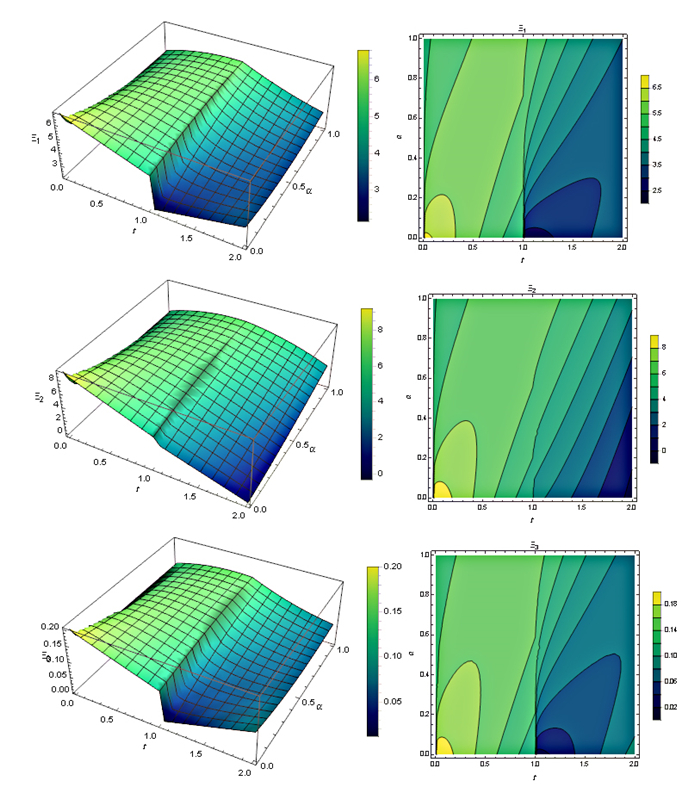
Figure 8.
The NR with
$ k=2, M=9, h=2, \theta =\frac{1}{8} $ $ \alpha (t) \in (0, 1) $ -
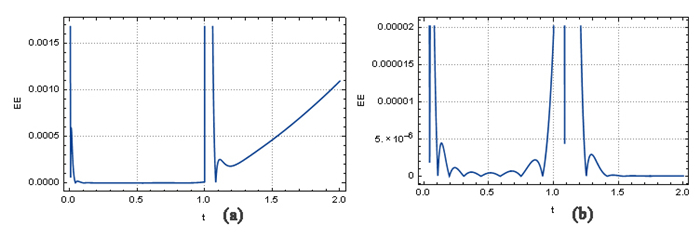
Figure 9.
The EE with
$ k=2, M=9, h=2, \theta =\frac{1}{8} $ $ (a): $ $ (b): $ -
Figure 10.
The NR with
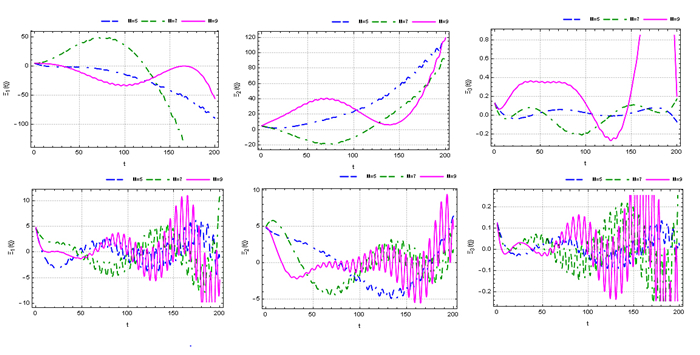
$ k=1, h=200, \theta =1 $ $ M=5, 7, 9 $ -
Figure 11.
The NR with
$ \theta =1, $ $ k=1, h=1, $ -
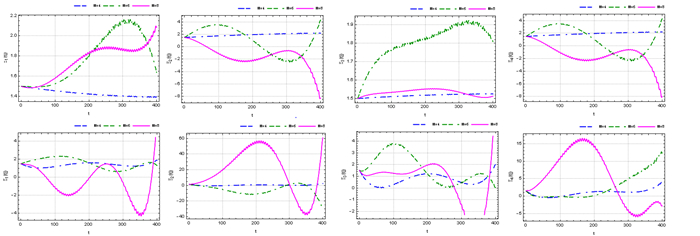
Figure 12.
The NR for up:
$ \theta =\frac{2}{3} $ $ \theta =1 $ $ k=1, h=400, $