| Citation: |
Xiaoling Xu, Xinyi Xu, Beiqing Gu, Ronghua Wang. STUDY ON THE GENERALIZED THREE-PARAMETER LINDLEY DISTRIBUTION[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3581-3609. doi: 10.11948/20240136
|
STUDY ON THE GENERALIZED THREE-PARAMETER LINDLEY DISTRIBUTION
-
Abstract
This paper introduces a new life distribution, the generalized three-parameter Lindley distribution, derived as a product of the inverse power law model and the generalized two-parameter Lindley distribution in a progressive stress accelerated life testing scenario. The study presents the graphical characteristics of the density function, failure rate function, mean failure rate function, and mean residual life function. Point estimates for the three parameters are provided through logarithmic transformation. The paper concludes with two practical examples demonstrating the application of this method.
-
-
References
[1] M. M. E. Abd El-Monsef, A new Lindley distribution with location parameter, Communications in Statistics-Theory and Methods, 2016, 45(17), 5204–5219. doi: 10.1080/03610926.2014.941496 [2] M. M. E. Abd El-Monsef, W. A. Hassanein and N. M. Kilany, Erlang-Lindley distribution, Communications in Statistics-Theory and Methods, 2017, 46(19), 9494–9506. doi: 10.1080/03610926.2016.1212069 [3] M. Ahsanullah, M. E. Ghitany and D. K. Al-Mutairi, Characterization of Lindley distribution by truncated moments, Communications in Statistics-Theory and Methods, 2017, 46(12), 6222–6227. doi: 10.1080/03610926.2015.1124117 [4] A. Algarni, On a new generalized Lindley distribution: Properties estimation and applications, PLoS ONE, 2021, 16(2), 1–19. [5] T. Arslan, S. Acitas and B. Senoglu, Generalized Lindley and power Lindley distributions for modeling the wind speed data, Energy Conversion and Management, 2017, 152, 300–311. doi: 10.1016/j.enconman.2017.08.017 [6] A. Asgharzadeh, S. Nadarajah and F. Sharafi, Weibull Lindley distribution, Revstat-Statistical Journal, 2018, 16(1), 87–113. [7] S. K. Ashour and M. A. Eltehiwy, Exponentiated power Lindley distribution, Journal of Advanced Research, 2015, 6(6), 895–905. doi: 10.1016/j.jare.2014.08.005 [8] K. V. P. Barco, J. Mazucheli and V. Janeiro, The inverse power Lindley distribution, Communications in Statistics-Simulation and Computation, 2017, 46(8), 6308–6323. doi: 10.1080/03610918.2016.1202274 [9] M. Borah and J. Hazarika, A new quasi Poison-Lindley distribution: Properties and applications, Journal of Statistical Theory and Applications, 2017, 16(4), 576–588. doi: 10.2991/jsta.2017.16.4.11 [10] C. Chesneau, L. Tomy and M. Jose, Wrapped modified Lindley distribution, Journal of Statistics and Management Systems, 2021, 24(5), 1025–1040. doi: 10.1080/09720510.2020.1796313 [11] Y. Dai, Statistical Analysis of Lindley Distribution, Master Dissertation of Shanghai Normal University, 2018. [12] Y. Dai, R. Wang and X. Xu, Statistical analysis of Lindley distribution under type-I censoring sample, Statistics and Decision, 2018(1), 84–87. [13] M. El-Morshedy, M. S. Eliwa and H. Nagy, A new two-parameter exponentiated discrete Lindley distribution: Properties, estimation and applications, Journal of Applied Statistics, 2020, 47(2), 354–375. doi: 10.1080/02664763.2019.1638893 [14] M. Ghica, N. D. Poesina and I. Prasacu, Exponentiated power quasi Lindley distribution, submodels and some properties, Review of the Air Force Academy, 2017, 15(2), 75–84. doi: 10.19062/1842-9238.2017.15.2.10 [15] M. E. Ghitany, D. K. Al-Mutairi, N. Balakrishnan and L. J. A1-Enezi, Power Lindley distribution and associated inference, Computational Statistics and Data Analysis, 2013, 64, 20–33. doi: 10.1016/j.csda.2013.02.026 [16] M. E. Ghitany, D. K. Al-Mutairi and S. Nadarajah, Zero-truncated Poisson-Lindley distribution and its application, Mathematics and Computers in Simulation, 2008, 79(3), 279–287. doi: 10.1016/j.matcom.2007.11.021 [17] M. E. Ghitany, F. Alqallaf, D. K. Al-Mutairi and H. A. Husain, A two-parameter weighted Lindley distribution and its applications to survival data, Mathematics and Computers in Simulation, 2011, 81(6), 1190–1201. doi: 10.1016/j.matcom.2010.11.005 [18] M. E. Ghitany, B. Atieh and S. Nadarajah, Lindley distribution and its application, Mathematics and Computers in Simulation, 2008, 78(4), 493–506. doi: 10.1016/j.matcom.2007.06.007 [19] T. Hussain, M. Aslam and M. Ahmad, A two parameter discrete Lindley distribution, Revista Colombiana de Estadistica, 2016, 39(1), 45–61. doi: 10.15446/rce.v39n1.55138 [20] S. Joshi and J. Kanichukattu, Wrapped Lindley distribution, Communications in Statistics-Theory and Methods, 2018, 47(5), 1013–1021. doi: 10.1080/03610926.2017.1280168 [21] S. A. Kemaloglu and M. Yilmaz. Transmuted two-parameter Lindley distribution, Communications in Statistics-Theory and Methods, 2017, 46(23), 11866–11879. doi: 10.1080/03610926.2017.1285933 [22] A. Khodadadi, M. Shirazi, S. Geedipally and D. Lord, Evaluating alternative variations of Negative Binormial-Lindley distribution for modelling crash data, Transportmetrica A: Transport Science, 2022, 1–22. [23] C. S. Kumar and R. Jose, On double Lindley distribution and some of its properties, American Journal of Mathematical and Management Sciences, 2019, 38(1), 23–43. doi: 10.1080/01966324.2018.1480437 [24] D. V. Lindley, Fiducial distributions and Bayes' theorem, Journal of the Royal Statistical Society, Series B: Methodological, 1958, 20(1), 102–107. doi: 10.1111/j.2517-6161.1958.tb00278.x [25] H. Lv, L. Gao and C. Chen, Ailamujia distribution and its application in support data analysis, Journal of Academy of Armored Force Engineering, 2000, 16(3), 48–52. [26] E. Mahmoudi and H. Zakerzadeh, Generalized Poisson-Lindley distribution, Communications in Statistics-Theory and Methods, 2010, 39(10), 1785–1798. doi: 10.1080/03610920902898514 [27] I. Makhdoom, P. Nasiri and A. Pak, Bayesian approach for the reliability parameter of power Lindley distribution, International Journal of System Assurance Engineering and Management, 2016, 7(3), 341–355. [28] R. Maya and M. R. Irshad, New extended generalized Lindley distribution: Properties and Applications, Statistica, 2017, 2017(1), 33–52. [29] J. Mazucheli and J. A. Achcar, The Lindley distribution applied to competing risks lifetime data, Computer Methods and Programs in Biomedicine, 2011, 104(2), 188–192. doi: 10.1016/j.cmpb.2011.03.006 [30] M. Mesfioui and A. M. Abouammoh, On a multivariate Lindley distribution, Communications in Statistics-Theory and Methods, 2017, 46(16), 8027–8045. doi: 10.1080/03610926.2016.1171355 [31] M. Naderi, A. Arabpour and A. Jamalizadeh, Multivariate normal mean-variance mixture distribution based on Lindley distribution, Communications in Statistics-Simulation and Computation, 2018, 47(4), 1179–1192. doi: 10.1080/03610918.2017.1307400 [32] S. Nedjar and H. Zeghdoudi, On gamma Lindley distribution: Properties and simulations, Journal of Computational and Applied Mathematics, 2016, 298, 167–174. doi: 10.1016/j.cam.2015.11.047 [33] W. Nelson, Accelerated life testing-step-stress models and data analyses, IEEE Transactions on Reliability, 1980, R–29(2), 103–108. [34] W. Nelson, Accelerated testing: Statistical models, test plans, and data analysis, John Wiley & Sons, Inc, 2004, 507–509. [35] J. Nie and W. Gui, Parameter estimation of Lindley distribution based on progressive type-II censored competing risks data with binomial removals, Mathmatics, 2019, 7(7), 646–659. [36] B. Oluyede, G. Warahena-Liyanage and M. Pararai, A new class of generalized Power Lindley distribution with applications to lifetime data, Theoretical Mathematics and Applications, 2015, 5(1), 53–96. [37] H. Papageorgiou and M. Vardaki, Bivariate discrete Poisson-Lindley distributions, Journal of Statistical Theory and Practice, 2022, 16(2), 1–23. [38] R. Roozegar and S. Nadarajah, On a generalized lindley distribution, statistica, 2017, 77(2), 149–157. [39] M. Sankaran, The discrete Poisson-Lindley distribution, Biometrics, 1970, 26(1), 145–149. [40] R. Shanker, K. K. Shukla, R. Shanker and T. A. Leonida, A three-Parameter Lindley distribution, American Journal of Mathematics and Statistics, 2017, 7(1), 15–26. [41] V. K. Sharma, S. K. Singh, U. Singh and V. Agiwal, The inverse Lindley distribution: A stressstrength reliability model with application to head and neck cancer data, Journal of Industrial and Production Engineering, 2015, 32(3), 162–173. [42] D. S. Shibu and M. R. Irshad, Extended new generalized Lindley distribution, Statistica, 2016, 76(1), 41–56. [43] M. Shrahili, N. Alotaibi, D. Kumar and A. R. Shafay, Inference on exponentiated power Lindley distribution based on order statistics with application, Complexity, 2020, 1–14. [44] A. Thongteeraparp and A. Volodin, Parameter estimation of the negative binomial-new weighted Lindley distribution by the method of maximum likelihood, Journal of Mathematics, 2020, 41(3), 430–434. [45] M. Yilmaz, M. Hameldarbandi and S. A. Kemaloglu, Exponential-modified discrete Lindley distribution, Springer Plus, 2016, 5, 1660–1680. [46] H. Zeghdoudi and S. Nedjar, A pseudo Lindley distribution and its application, The Statistics and Probability African Society, 2016, 11(1), 923–932. -
-
Figures(32)
Export File
Citation
Xiaoling Xu, Xinyi Xu, Beiqing Gu, Ronghua Wang. STUDY ON THE GENERALIZED THREE-PARAMETER LINDLEY DISTRIBUTION[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3581-3609. doi: 10.11948/20240136
Format
Content
DownLoad:
-
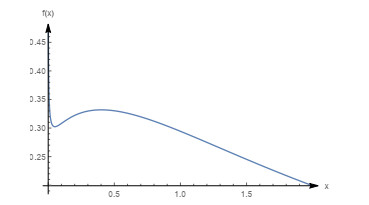
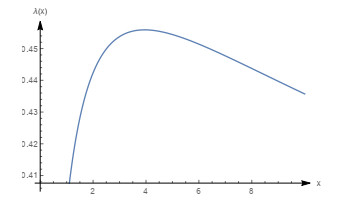
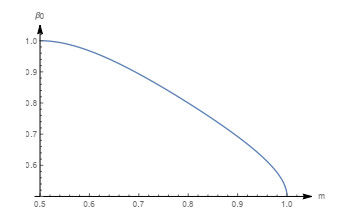
Figure 1.
Graph of
$ \beta_{0} $ $ m(0.5 \leq m \leq 1) $ -
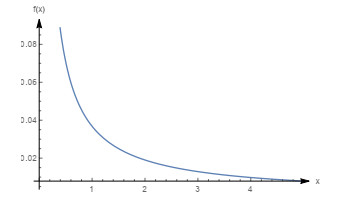
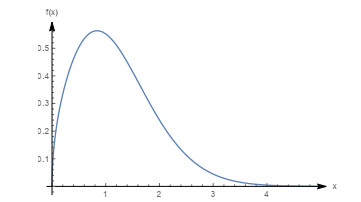
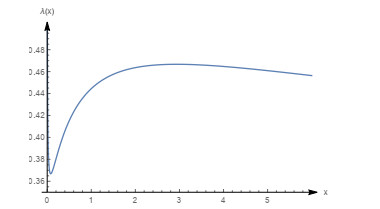
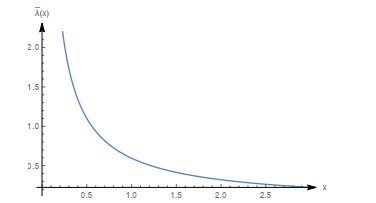
Figure 2.
Graph of the density function with
$ m=0.1, \beta=0.5, \theta=1 $ -
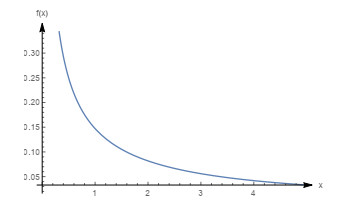
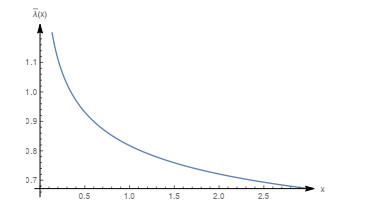
Figure 3.
Graph of the density function with
$ m=0.4, \beta=0.5, \theta=1 $ -
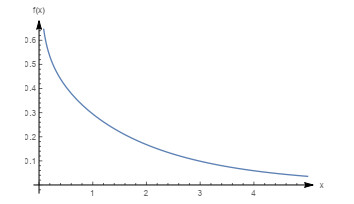
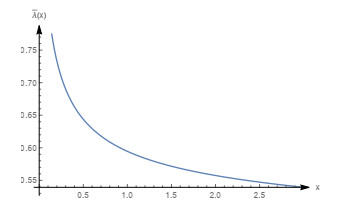
Figure 4.
Graph of the density function with
$ m=0.8, \beta=0.5, \theta=1 $ $ (\beta_{0}=0.8, \frac{m}{3 m-1}=\frac{4}{7} ) $ -
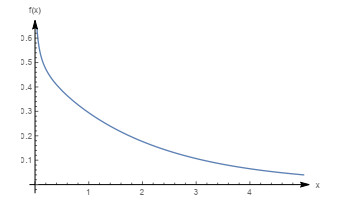
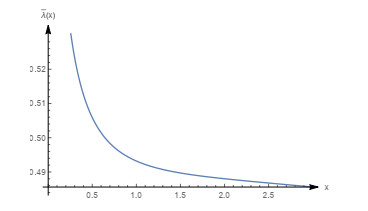
Figure 5.
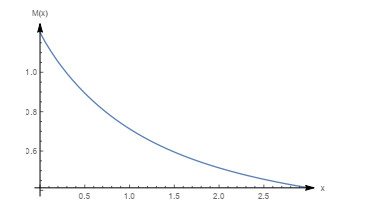
Graph of the density function with
$ m=0.8, \beta=0.6, \theta=1 $ $ (\beta_{0}=0.8, \frac{m}{3 m-1}=\frac{4}{7} ) $ -
Figure 6.
Graph of the density function with
$ m=0.8, \beta=0.85, \theta=1 $ $ (\beta_{0}=0.8, \frac{m}{3 m-1}=\frac{4}{7} ) $ -
Figure 7.
Graph of the density function with
$ m=1.5, \beta=0.5, \theta=1 $ -
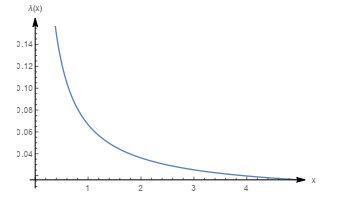
Figure 8.
Graph of the failure rate function with
$ m=0.1, \beta=0.5, \theta=1 $ -
Figure 9.
Graph of the failure rate function with
$ m=0.8, \beta=0.2, \theta=1 $ -
Figure 10.
Graph of the failure rate function with
$ m=0.8, \beta=1, \theta=1 $ -
Figure 11.
Graph of the failure rate function with
$ m=0.8, \beta=0.6, \theta=1 $ -
Figure 12.
Graph of the failure rate function with
$ m=0.8, \beta=0.8, \theta=1 $ -
Figure 13.
Graph of the failure rate function with
$ m=1.5, \beta=0.5, \theta=1 $ -
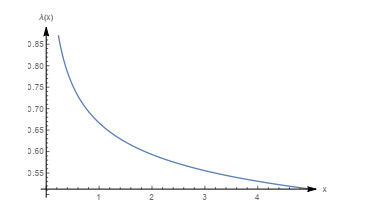
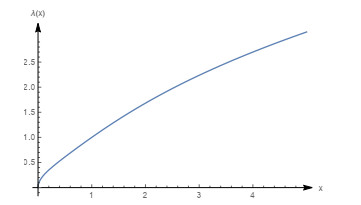
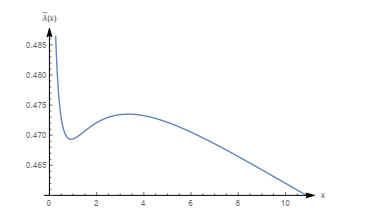
Figure 14.
Graph of the mean failure rate function with
$ m=0.1, \beta=0.5, \theta=1 $ -
Figure 15.
Graph of the mean failure rate function with
$ m=0.8, \beta=0.2, \theta=1 $ -
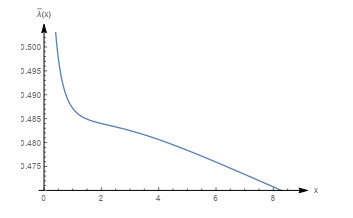
Figure 16.
Graph of the mean failure rate function with
$ m=0.8, \beta=0.5, \theta=1 (\beta_0=0.656402) $ -
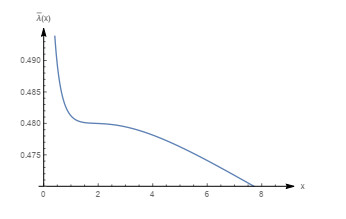
Figure 17.
Graph of the mean failure rate function with
$ m=0.8, \beta=0.66, \theta=1 (\beta_0=0.656402) $ -
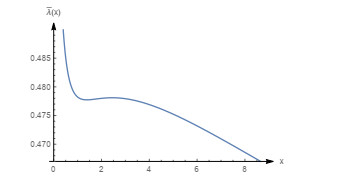
Figure 18.
Graph of the mean failure rate function with
$ m=0.8, \beta=0.67, \theta=1 (\beta_0=0.656402) $ -
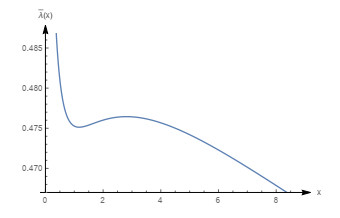
Figure 19.
Graph of the mean failure rate function with
$ m=0.8, \beta=0.68, \theta=1 (\beta_0=0.656402) $ -
Figure 20.
Graph of the mean failure rate function with
$ m=0.8, \beta=0.685, \theta=1 (\beta_0=0.656402) $ -
Figure 21.
Graph of the mean failure rate function with
$ m=0.8, \beta=0.69, \theta=1 (\beta_0=0.656402) $ -
Figure 22.
Graph of the mean failure rate function with
$ m=0.8, \beta=0.7, \theta=1 (\beta_0=0.656402) $ -
Figure 23.
Graph of the mean failure rate function with
$ m=1.5, \beta=0.5, \theta=1 $ -
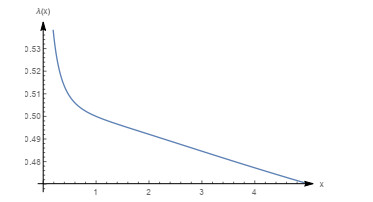
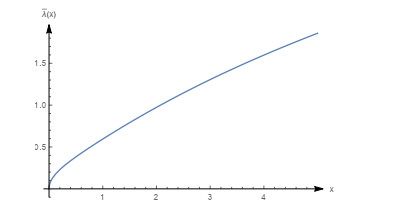
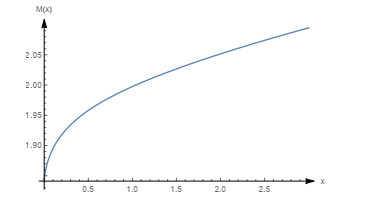
Figure 24.
Graph of the mean residual life with
$ m=0.1, \beta=0.5, \theta=1 $ -
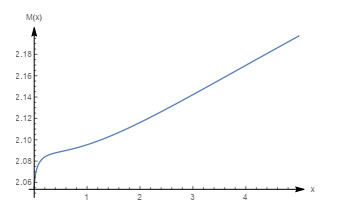
Figure 25.
Graph of the mean residual life with
$ m=0.8, \beta=0.3, \theta=1 $ -
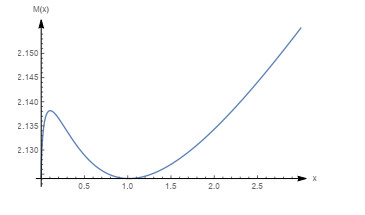
Figure 26.
Graph of the mean residual life with
$ m=0.8, \beta=0.5, \theta=1 $ -
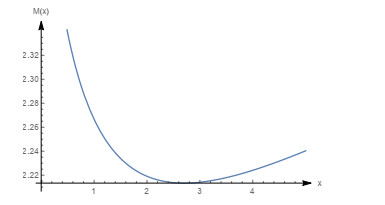
Figure 27.
Graph of the mean residual life with
$ m=0.8, \beta=0.65, \theta=1 $ -
Figure 28.
Graph of the mean residual life with
$ m=0.8, \beta=0.7, \theta=1 $ -
Figure 29.
Graph of the mean residual life with
$ m=0.8, \beta=1, \theta=1 $ -
Figure 30.
Graph of the mean residual life with
$ m=1.5, \beta=0.5, \theta=1 $ -
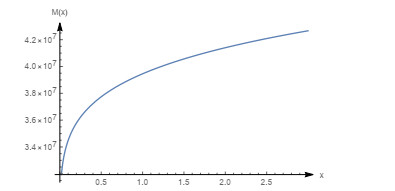
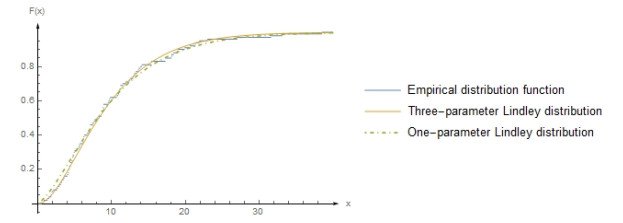
Figure 31.
Empirical distribution function and theoretical distribution functions for case 6.1.
-
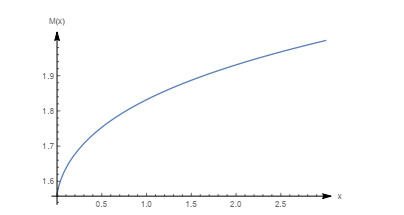
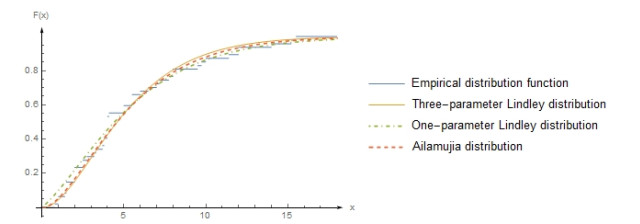
Figure 32.
Empirical distribution function and theoretical distribution functions for case 6.2.