| Citation: | Shweta, Saddam Hussain, Rajesh Kumar, Rajesh Kumar. AN IMPROVED VERSION OF HOMOTOPY PERTURBATION METHOD FOR MULTI-DIMENSIONAL BURGERS' EQUATIONS[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 517-546. doi: 10.11948/20240143 |
AN IMPROVED VERSION OF HOMOTOPY PERTURBATION METHOD FOR MULTI-DIMENSIONAL BURGERS' EQUATIONS
-
Abstract
The accelerated homotopy perturbation Elzaki transform method (AHPETM), which is based on the homotopy perturbation method (HPM), is used in this article to solve the Burgers equation and system of Burgers equations. AHPETM presents the Elzaki integral transform as a pre-treatment in combination with the decomposition of nonlinear variables to speed up the convergence of the HPM solution to its precise values. When the suggested method's findings are compared to HPM's, the results show a considerable improvement. Theoretical convergence analysis and error estimations are also crucial in this work. Multiple numerical examples of 1D, 2D, and 3D Burgers equations, as well as systems of 1D and 2D Burgers equations, are examined to confirm the method's accuracy. Interestingly, the proposed approach offers the closed-form results to most of the problems, which are essentially the exact solutions.
-

-
References
[1] W. M. Abd-Elhameed, Novel expressions for the derivatives of sixth kind chebyshev polynomials: Spectral solution of the non-linear one-dimensional burgers' equation, Fractal and Fractional, 2021, 5(2), 53. doi: 10.3390/fractalfract5020053 [2] A. Adem, B. Muatjetjeja and T. S. Moretlo, An extended (2+1)-dimensional coupled burgers system in fluid mechanics: Symmetry reductions, kudryashov method, conservation laws, International Journal of Theoretical Physics, 2023, 62(2), 38. doi: 10.1007/s10773-023-05298-9 [3] S. Albeverio, A. Korshunova and O. Rozanova, A probabilistic model associated with the pressureless gas dynamics, Bulletin des Sciences Mathematiques, 2013, 137(7), 902–922. doi: 10.1016/j.bulsci.2013.05.001 [4] M. A. Al-Jawary, M. M. Azeez and G. H. Radhi, Analytical and numerical solutions for the nonlinear burgers and advection–diffusion equations by using a semi-analytical iterative method, Computers & Mathematics with Applications, 2018, 76(1), 155–171. [5] I. Ali, S. Haq, K. S. Nisar and D. Baleanu, An efficient numerical scheme based on lucas polynomials for the study of multidimensional burgers-type equations, Advances in Difference Equations, 2021, 2021(1), 1–24. doi: 10.1186/s13662-020-03162-2 [6] G. Arora, S. Hussain and R. Kumar, Comparison of variational iteration and adomian decomposition methods to solve growth, aggregation and aggregation-breakage equations, Journal of Computational Science, 2023, 67, 101973. doi: 10.1016/j.jocs.2023.101973 [7] G. Arora, R. Kumar and Y. Mammeri, Homotopy perturbation and adomian decomposition methods for condensing coagulation and lifshitz-slyzov models, GEM-International Journal on Geomathematics, 2023, 14(1), 4. doi: 10.1007/s13137-023-00215-y [8] I. Asmouh, M. El-Amrani, M. Seaid and N. Yebari, High-order isogeometric modified method of characteristics for two-dimensional coupled burgers' equations, International Journal for Numerical Methods in Fluids, 2022, 94(6), 608–631. doi: 10.1002/fld.5068 [9] M. Ben-Romdhane and H. Temimi, An iterative numerical method for solving the lane–emden initial and boundary value problems, International Journal of Computational Methods, 2018, 15(4), 1850020. doi: 10.1142/S0219876218500202 [10] M. P. Bonkile, A. Awasthi, C. Lakshmi, et al., A systematic literature review of burgers' equation with recent advances, Pramana, 2018, 90, 1–21. doi: 10.1007/s12043-017-1492-y [11] J. M. Burgers, A mathematical model illustrating the theory of turbulence, Advances in Applied Mechanics, 1948, 1, 171–199. [12] Y. Çenesiz, D. Baleanu, A. Kurt and O. Tasbozan, New exact solutions of burgers' type equations with conformable derivative, Waves in Random and Complex Media, 2017, 27(1), 103–116. doi: 10.1080/17455030.2016.1205237 [13] M. Dehghan, A. Hamidi and M. Shakourifar, The solution of coupled burgers' equations using adomian–pade technique, Applied Mathematics and Computation, 2007, 189(2), 1034–1047. doi: 10.1016/j.amc.2006.11.179 [14] M. Dehghan, Y. Rahmani, D. D. Ganji, et al., Convection–radiation heat transfer in solar heat exchangers filled with a porous medium: Homotopy perturbation method versus numerical analysis, Renewable Energy, 2015, 74, 448–455. doi: 10.1016/j.renene.2014.08.044 [15] T. M. Elzaki, Application of new transform"elzaki transform" to partial differential equations, Global Journal of Pure and Applied Mathematics, 2011, 7(1), 65–70. [16] T. M. Elzaki, The new integral transform elzaki transform, Global Journal of Pure and Applied Mathematics, 2011, 7(1), 57–64. [17] T. M. Elzaki, et al., On the new integral transform"elzaki transform" fundamental properties investigations and applications, Global Journal of Mathematical Sciences: Theory and Practical, 2012, 4(1), 1–13. [18] T. M. Elzaki and H. Kim, The solution of burger's equation by elzaki homotopy perturbation method, Applied Mathematical Sciences, 2014, 8(59), 2931–2940. [19] S. E. Esipov, Coupled burgers equations: A model of polydispersive sedimentation, Physical Review E, 1995, 52(4), 3711. doi: 10.1103/PhysRevE.52.3711 [20] D. Ganji and A. Sadighi, Application of he's homotopy-perturbation method to nonlinear coupled systems of reaction-diffusion equations, Int. J. of Nonlinear Sciences and Numerical Simulation, 2006, 7(4), 411–418. [21] Y. Guo, Y. -F. Shi and Y. -M. Li, A fifth-order finite volume weighted compact scheme for solving one-dimensional burgers' equation, Applied Mathematics and Computation, 2016, 281, 172–185. doi: 10.1016/j.amc.2016.01.061 [22] J. He, A new approach to nonlinear partial differential equations, Communications in Nonlinear Science and Numerical Simulation, 1997, 2(4), 230–235. [23] J. -H. He, Application of homotopy perturbation method to nonlinear wave equations, Chaos, Solitons & Fractals, 2005, 26(3), 695–700. [24] S. Hussain, G. Arora and R. Kumar, Semi-analytical methods for solving non-linear differential equations: A review, Journal of Mathematical Analysis and Applications, 2023, 127821. [25] S. Hussain, G. Arora and R. Kumar, An efficient semi-analytical technique to solve multi-dimensional burgers' equation, Computational and Applied Mathematics, 2024, 43(1), 11. [26] S. Hussain and R. Kumar, Elzaki projected differential transform method for multi-dimensional aggregation and combined aggregation-breakage equations, Journal of Computational Science, 2024, 75, 102211. [27] A. Hussein and H. Kashkool, L2-optimal order error for two-dimensional coupled burgers'equations by weak galerkin finite element method, TWMS Journal of Applied and Engineering Mathematics, 2022, 12(1), 34. [28] M. Inc, On numerical solution of burgers' equation by homotopy analysis method, Physics Letters A, 2008, 372(4), 356–360. [29] S. Jasrotia and P. Singh, Accelerated homotopy perturbation elzaki transformation method for solving nonlinear partial differential equations, in {Journal of Physics: Conference Series}, 2267, IOP Publishing, 2022, 012106. [30] Y. -C. Jiao, Y. Yamamoto, C. Dang and Y. Hao, An aftertreatment technique for improving the accuracy of adomian's decomposition method, Computers & Mathematics with Applications, 2002, 43(6–7), 783–798. [31] S. Kaushik, S. Hussain and R. Kumar, Laplace transform-based approximation methods for solving pure aggregation and breakage equations, Mathematical Methods in the Applied Sciences, 2023, 46(16), 17402–17421. [32] K. A. Koroche, et al., Numerical solution of in-viscid burger equation in the application of physical phenomena: The comparison between three numerical methods, Int. J. of Mathematics and Mathematical Sciences, 2022, 2022. [33] R. Mittal and S. Kumar, A numerical study of stationary solution of viscous burgers' equation using wavelet, International Journal of Computer Mathematics, 2010, 87(6), 1326–1337. [34] V. Mukundan, A. Awasthi and V. Aswin, Multistep methods for the numerical simulation of two-dimensional burgers' equation, Differential Equations and Dynamical Systems, 2019, 1–24. [35] Z. Odibat, An optimized decomposition method for nonlinear ordinary and partial differential equations, Physica A: Statistical Mechanics and its Applications, 2020, 541, 123323. [36] M. Ross and H. Bindra, Development of a subgrid-scale model for burgers turbulence using statistical mechanics-based methods, Physics of Fluids, 2023, 35(12). [37] V. K. Srivastava, N. Mishra, S. Kumar, et al., Reduced differential transform method for solving (1+n)–dimensional burgers' equation, Egyptian Journal of Basic and Applied sciences, 2014, 1(2), 115–119. [38] M. Tamsir and V. K. Srivastava, A semi-implicit finite-difference approach for two-dimensional coupled burgers' equations, International Journal of Scientific & Engineering Research, 2011, 2(6), 46–51. [39] H. Temimi, A. R. Ansari and A. M. Siddiqui, An approximate solution for the static beam problem and nonlinear integro-differential equations, Computers & Mathematics with Applications, 2011, 62(8), 3132–3139. [40] H. Temimi, M. Ben-Romdhane, S. El-Borgi and Y. -J. Cha, Time-delay effects on controlled seismically excited linear and nonlinear structures, International Journal of Structural Stability and Dynamics, 2016, 16(7), 1550031. [41] A. -M. Wazwaz, The tanh method for traveling wave solutions of nonlinear equations, Applied Mathematics and Computation, 2004, 154(3), 713–723. [42] A. -M. Wazwaz and A. -M. Wazwaz, Solitary waves theory, Partial Differential Equations and Solitary Waves Theory, 2009, 479–502. [43] D. Zeidan, C. K. Chau, T. -T. Lu and W. -Q. Zheng, Mathematical studies of the solution of burgers' equations by adomian decomposition method, Mathematical Methods in the Applied Sciences, 2020, 43(5), 2171–2188. [44] H. Zhu, H. Shu and M. Ding, Numerical solutions of two-dimensional burgers' equations by discrete adomian decomposition method, Computers & Mathematics with Applications, 2010, 60(3), 840–848. -
-
-
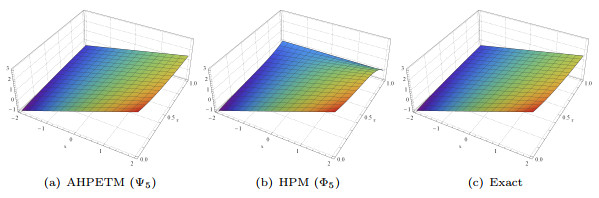
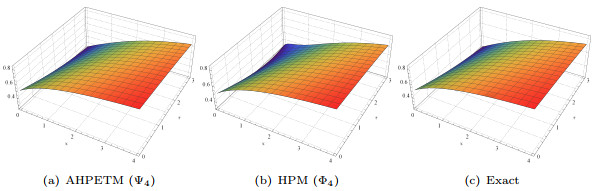
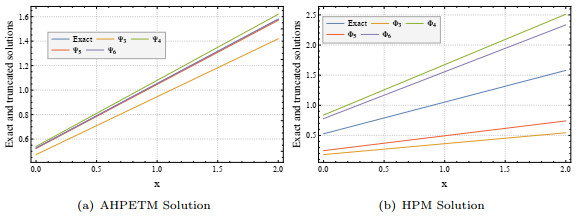
Figure 1.
Comparison of approximated and exact solutions when
$ a,b=1 $ $ 5.1 $ -
Figure 2.
Approximated and exact solutions when
$ a,b=1 $ $ 5.1 $ -
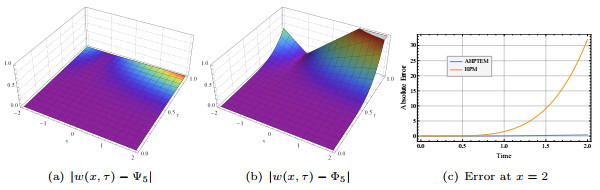
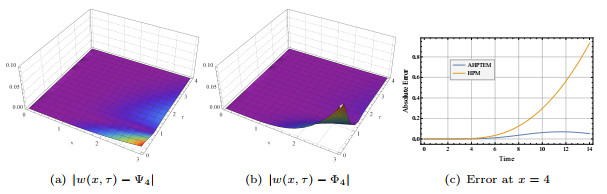
Figure 3.
Errors for AHPETM and HPM when
$ a,b=1 $ $ 5.1 $ -
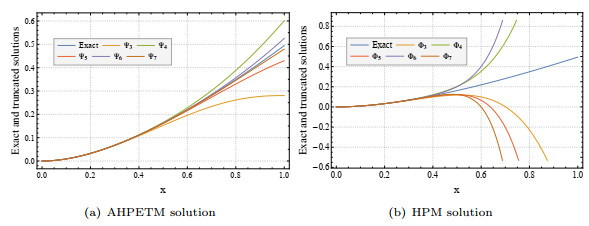
Figure 4.
Comparison of approximated series and exact solutions when
$ a=1 $ $ 5.2 $ -
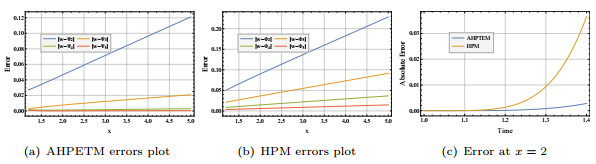
Figure 5.
Errors for AHPETM and HPM when
$ a=1 $ $ 5.2 $ -
Figure 6.
Approximated and exact solutions when
$ a, b, c = 1, d = 2 $ $ 5.3 $ -
Figure 7.
Errors for AHPETM and HPM when
$ a, b, c = 1, d = 2 $ $ 5.3 $ -
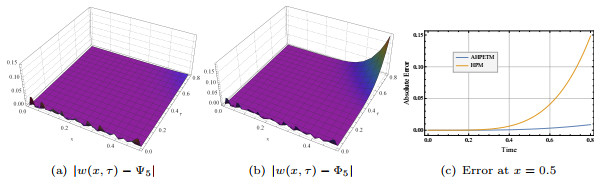
Figure 8.
3D Errors for AHPETM and HPM when
$ c = 1 $ $ 5.5 $ -
Figure 9.
Error plots when
$ c = 1 $ $ 5.5 $ -
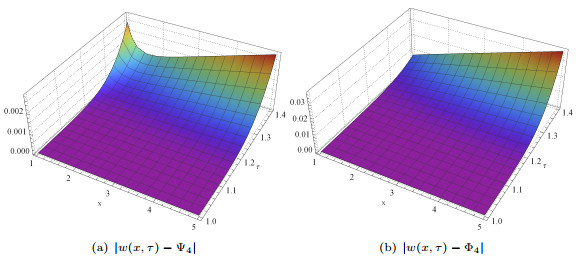
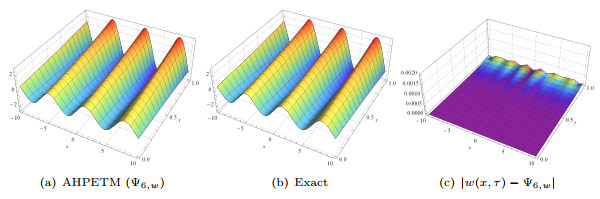
Figure 10.
Approximated and exact solutions, absolute error plots for
$ w(x,\tau) $ $ 5.6 $ -
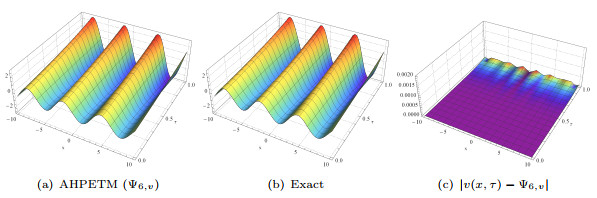
Figure 11.
Approximated and exact solutions, absolute error plots for
$ v(x,\tau) $ $ 5.6 $ -
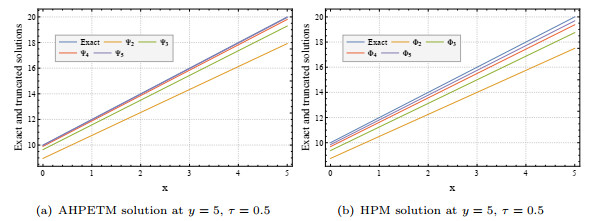
Figure 12.
Comparison of approximated solutions with exact solution for Example
$ 5.7 $ -
Figure 13.
Absolute error for AHPETM and HPM for Example
$ 5.7 $ -
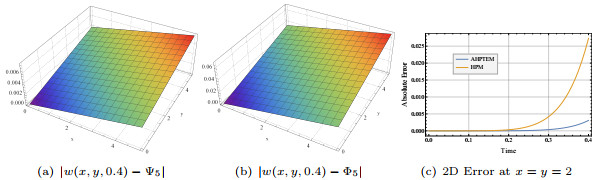
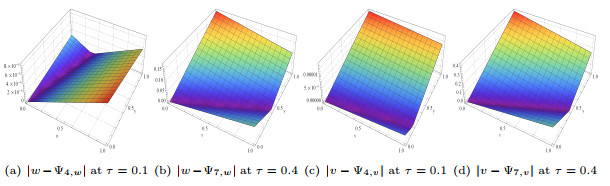
Figure 14.
Absolute error plots at
$ \tau=0.1 $ $ \tau=0.4 $ $ 5.8 $ -
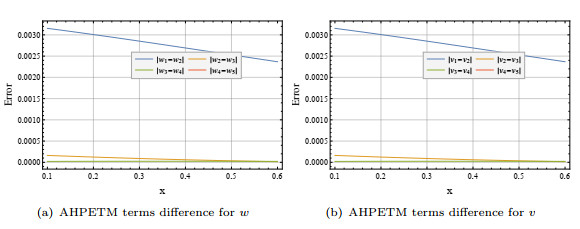
Figure 15.
Consecutive terms difference of series solutions for
$ w(x,0.3,0.1) $ $ v(x,0.3,0.1) $ $ 5.9 $ -
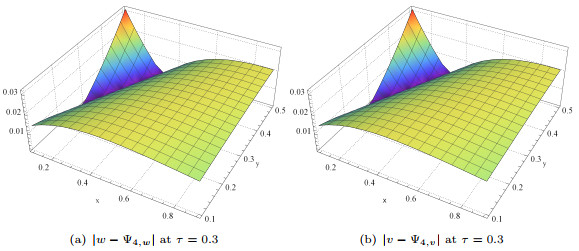
Figure 16.
Absolute error plots of AHPETM solutions for
$ w $ $ v $ $ 5.9 $




 DownLoad:
DownLoad: