| Citation: |
Panpan Wang, Xiufang Feng, Shangqin He. LIE SYMMETRY REDUCTION FOR (2+1)-DIMENSIONAL FRACTIONAL SCHRÖDINGER EQUATION[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 502-516. doi: 10.11948/20240133
|
LIE SYMMETRY REDUCTION FOR (2+1)-DIMENSIONAL FRACTIONAL SCHRÖDINGER EQUATION
-
Abstract
This study investigates Lie symmetry analysis, exact solutions, and conservation laws for a (2+1)-dimensional fractional Schrödinger equation. The original equations have been reduced to fractional ODEs employing the obtained vector field. For the considered equation, exact solutions are also established. Furthermore, the resulting exact solutions are demonstrated for convergence. Conservation laws for this equation have been investigated employing the Ibragimov theorem.
-
-
References
[1] M. Abdel Aal and O. Abu Arqub, Lie analysis and laws of conservation for the two-dimensional model of Newell–Whitehead–Segel regarding the Riemann operator fractional scheme in a time-independent variable, Arab Journal of Basic and Applied Sciences, 2023, 30(1), 55–67. doi: 10.1080/25765299.2023.2172840 [2] O. Abu Arqub, T. Hayat and M. Alhodaly, Analysis of lie symmetry, explicit series solutions, and conservation laws for the nonlinear time-fractional phi-four equation in two-dimensional space, International Journal of Applied and Computational Mathematics, 2022, 8(3), 145–161. doi: 10.1007/s40819-022-01334-0 [3] R. Al-Deiakeh, O. Abu Arqub and M. Al-Smadi, Lie symmetry analysis, explicit solutions, and conservation laws of the time-fractional Fisher equation in two-dimensional space, Journal of Ocean Engineering and Science, 2022, 7(4), 345–352. doi: 10.1016/j.joes.2021.09.005 [4] M. Al-Smadi, O. Abu Arqub and S. Momani, Numerical computations of coupled fractional resonant Schrödinger equations arising in quantum mechanics under conformable fractional derivative sense, Physica Scripta, 2020, 95(7), 075218–075239. doi: 10.1088/1402-4896/ab96e0 [5] M. N. Alam and C. Tunç, The new solitary wave structures for the (2+1)-dimensional time-fractional Schrodinger equation and the space-time nonlinear conformable fractional Bogoyavlenskii equations, Alexandria Engineering Journal, 2020, 59, 2221–2232. doi: 10.1016/j.aej.2020.01.054 [6] O. A. Arqub, Application of residual power series method for the solution of time-fractional Schrödinger equations in one-dimensional space, Fundamenta Informaticae, 2019, 166(2), 87–110. doi: 10.3233/FI-2019-1795 [7] E. Buckwar and Y. Luchko, Invariance of a partial differential equation of fractional order under the Lie group of scaling transformations, Journal of Mathematical Analysis and Applications, 1998, 227(1), 81–97. doi: 10.1006/jmaa.1998.6078 [8] R. K. Gazizov, A. A. Kasatkin and S. Y. Lukashchuk, Symmetry properties of fractional diffusion equations, Physica Scripta, 2009, 2009(T136), 014016–014020. [9] M. S. Hashemi, A. Haji-Badali and F. Alizadeh, Classical and non-classical Lie symmetry analysis, conservation laws and exact solutions of the time-fractional Chen-Lee-Liu equation, Computational and Applied Mathematics, 2023, 42(2), 73–93. doi: 10.1007/s40314-023-02217-w [10] N. H. Ibragimov, A new conservation theorem, Journal of Mathematical Analysis and Applications, 2007, 333, 311–328. doi: 10.1016/j.jmaa.2006.10.078 [11] M. Inc, A. Yusuf and A. I. Aliyu, Lie symmetry analysis, explicit solutions and conservation laws for the space–time fractional nonlinear evolution equations, Physica A: Statistical Mechanics and its Applications, 2018, 496, 371–383. doi: 10.1016/j.physa.2017.12.119 [12] M. T. Islam, M. A. Akbar and J. F. Gómez-Aguilar, Assorted soliton structures of solutions for fractional nonlinear Schrodinger types evolution equations, Journal of Ocean Engineering and Science, 2022, 7, 528–535. doi: 10.1016/j.joes.2021.10.006 [13] C. Li, Q. Guo and M. Zhao, On the solutions of (2+1)-dimensional time-fractional Schrödinger equation, Applied Mathematics Letters, 2019, 94, 238–243. doi: 10.1016/j.aml.2019.02.033 [14] P. Olver, Application of Lie Group to Differential Equation, 1986, Springer. [15] X. Peng, Y. W. Zhao and X. Lü, Data-driven solitons and parameter discovery to the (2+1)-dimensional NLSE in optical fiber communications, Nonlinear Dynamics, 2024, 112, 1291–1306. doi: 10.1007/s11071-023-09083-5 [16] M. Rahioui, E. H. El Kinani and A. Ouhadan, Invariant Analysis, Approximate Solutions, and Conservation Laws for the Time Fractional Higher Order Boussinesq–Burgers System, Mathematical Methods in the Applied Sciences, 2024. [17] M. Rahioui, E. H. El Kinani and A. Ouhadan, Investigation of some time–space M-truncated partial differential equations: Lie symmetry analysis, exact solutions and conservation laws, International Journal of Applied and Computational Mathematics, 2024, 10(2), 1–20. [18] M. Rahioui, E. H. El Kinani and A. Ouhadan, Nonlocal residual symmetries, N-th Bäcklund transformations and exact interaction solutions for a generalized Broer-Kaup-Kupershmidt system, Zeitschrift für angewandte Mathematik und Physik, 2024, 75(2), 1–10. [19] S. T. R. Rizvi, K. Ali and S. Bashir, Exact soliton of (2+1)-dimensional fractional Schrödinger equation, Superlattices and Microstructures, 2017, 107, 234–239. doi: 10.1016/j.spmi.2017.04.029 [20] R. Sahadevan and T. Bakkyaraj, Invariant analysis of time fractional generalized Burgers and Korteweg–de Vries equations, Journal of mathematical analysis and applications, 2012, 393, 341–347. doi: 10.1016/j.jmaa.2012.04.006 [21] H. Triki and V. I. Kruglov, Propagation of dipole solitons in inhomogeneous highly dispersive optical-fiber media, Physical Review E, 2020, 101, 042220–042230. doi: 10.1103/PhysRevE.101.042220 [22] G. Wang, X. Liu and Y. Zhang, Lie symmetry analysis to the time fractional generalized fifth-order KdV equation, Communications in Nonlinear Science and Numerical Simulation, 2013, 18(9), 2321–2326. doi: 10.1016/j.cnsns.2012.11.032 -
-
Figures(2)
Export File
Citation
Panpan Wang, Xiufang Feng, Shangqin He. LIE SYMMETRY REDUCTION FOR (2+1)-DIMENSIONAL FRACTIONAL SCHRÖDINGER EQUATION[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 502-516. doi: 10.11948/20240133
Format
Content
DownLoad:
-
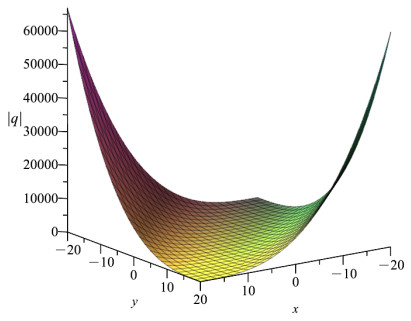
Figure 1.
Numerical simulation of power series solutions
$ |q| $ $ a_{0}=b_{0}=a_{1}=b_{1}=0.1 $ $ a-b=-1 $ $ \gamma=0.1 $ $ \alpha=0.8 $ -
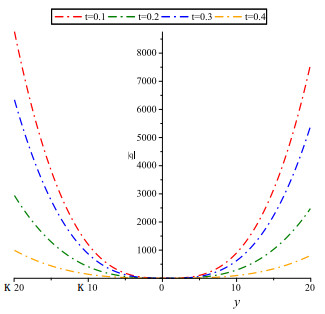
Figure 2.
Wave disseminate pattern along
$ y $ $ a_{0}=b_{0}=a_{1}=b_{1}=0.1 $ $ a-b=-1 $ $ \gamma=0.1 $ $ \alpha=0.8 $ $ x=0.2 $