| Citation: |
Rehana Naz, Gangwei Wang, Saba Irum. THE CLOSED-FORM SOLUTIONS OF A DIFFUSIVE SUSCEPTIBLE-INFECTIOUS-SUSCEPTIBLE EPIDEMIC MODEL[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 574-586. doi: 10.11948/20240175
|
THE CLOSED-FORM SOLUTIONS OF A DIFFUSIVE SUSCEPTIBLE-INFECTIOUS-SUSCEPTIBLE EPIDEMIC MODEL
-
Abstract
We establish the closed-form solutions of the Susceptible-Infectious-Susceptible (SIS) epidemic model with diffusion using Lie point symmetries. The model admits a four-dimensional Lie algebra. We use different combinations of Lie symmetries to construct the closed-form solutions. We consider appropriate initial and boundary conditions to explore the biological relevance of these closed-form solutions. We utilize the closed-form solutions to study the transmission dynamics of an influenza outbreak with Gaussian initial distributions. We plot graphs for the susceptible and infected populations. We consider the lower diffusion coefficient and higher diffusion coefficient cases to analyze the transmission dynamics of the influenza outbreak.
-
Keywords:
- Diffusive SIS model /
- Lie symmetries /
- closed-form solutions
-
-
References
[1] L. J. Allen, B. M. Bolker, Y. Lou and A. L. Nevai, Asymptotic profiles of the steady states for an SIS epidemic reaction-diffusion model, Discrete & Continuous Dynamical Systems, 2008, 21(1), 1. [2] G. W. Bluman and S. Kumei, Symmetries and Differential Equations, Springer, New York, 1989. [3] R. S. Cantrell and C. Cosner, Spatial Ecology via Reaction-Diffusion Equations, John Wiley & Sons, 2004. [4] B. Champagne, W. Hereman and P. Winternitz, The computer calculation of Lie point symmetries of large systems of differential equations, Computer Physics Communications, 1991, 66(2–3), 319–340. doi: 10.1016/0010-4655(91)90080-5 [5] A. F. Cheviakov, GeM software package for computation of symmetries and conservation laws of differential equations, Computer Physics Communications, 2007, 176(1), 48–61. doi: 10.1016/j.cpc.2006.08.001 [6] W. Ding, W. Huang and S. Kansakar, Traveling wave solutions for a diffusive SIS epidemic model, Discrete & Continuous Dynamical Systems-B, 2013, 18(5), 1291. [7] B. U. Haq and I. Naeem, First integrals and exact solutions of some compartmental disease models, Zeitschrift für Naturforschung A, 2019, 74(4), 293–304. doi: 10.1515/zna-2018-0450 [8] B. U. Haq and I. Naeem, First integrals and analytical solutions of some dynamical systems, Nonlinear Dynamics, 2019, 95(3), 1747–1765. doi: 10.1007/s11071-018-4657-4 [9] W. Hereman, SYMMGRP. MAX and other symbolic programs for lie symmetry analysis of partial differential equation, Lectures in Appl. Math., 1993, 29, 241–257. [10] W. Hereman, Symbolic software for Lie symmetry analysis, CRC Handbook of Lie Group Analysis of Differential Equations, 1996, 3, 367–413. [11] W. Hereman, Review of symbolic software for Lie symmetry analysis, Mathematical and Computer Modelling, 1997, 25(8–9), 115–132. doi: 10.1016/S0895-7177(97)00063-0 [12] W. Huang, M. Han and K. Liu, Dynamics of an SIS reaction-diffusion epidemic model for disease transmission, Mathematical Biosciences & Engineering, 2010, 7(1), 51. [13] N. H. Ibragimov (Ed. ), CRC Handbook of Lie Group Analysis of Differential Equations, vols. 1–3, CRC Press, Boca Raton, FL, 1994–1996. [14] A. Källén, Thresholds and travelling waves in an epidemic model for rabies, Nonlinear Analysis: Theory, Methods & Applications, 1984, 8(8), 851–856. [15] A. Källén, P. Arcuri and J. D. Murray, A simple model for the spatial spread and control of rabies, Journal of Theoretical Biology, 1985, 116(3), 377–393. doi: 10.1016/S0022-5193(85)80276-9 [16] J. D. Murray and W. L. Seward, On the spatial spread of rabies among foxes with immunity, Journal of Theoretical Biology, 1992, 156(3), 327–348. doi: 10.1016/S0022-5193(05)80679-4 [17] J. D. Murray, E. A. Stanley and D. L. Brown, On the spatial spread of rabies among foxes, Proceedings of the Royal Society of London, Series B. Biological Sciences, 1986, 229(1255), 111–150. [18] R. Naz and M. Al-Raeei, Analysis of transmission dynamics of COVID-19 via closed-form solutions of a susceptible-infectious-quarantined-diseased model with a quarantine-adjusted incidence function, Mathematical Methods in the Applied Sciences, 2021, 44(14), 11196–11210. doi: 10.1002/mma.7481 [19] J. V. Noble, Geographic and temporal development of plagues, Nature, 1974, 250(5469), 726–729. doi: 10.1038/250726a0 [20] P. J. Olver, Applications of Lie Groups to Differential Equations, Second Edition, Springer Verlag, New York, NY, USA, 1993. [21] L. V. Ovsiannikov, Group Analysis of Differential Equations, Academic Press, New York, 1982. [22] R. Peng and S. Liu, Global stability of the steady states of an SIS epidemic reaction-diffusion model, Nonlinear Analysis: Theory, Methods & Applications, 2009, 71(1–2), 239–247. [23] T. M. Rocha Filho and A. Figueiredo, [SADE] a Maple package for the symmetry analysis of differential equations, Computer Physics Communications, 2011, 182(2), 467–476. [24] S. Ruan, Spatial-temporal dynamics in nonlocal epidemiological models, in Mathematics for Life Science and Medicine, Springer, Berlin, Heidelberg, 2007, 97–122. [25] M. Samsuzzoha, M. Singh and D. Lucy, Numerical study of a diffusive epidemic model of influenza with variable transmission coefficient, Applied Mathematical Modelling, 2011, 35(12), 5507–5523. [26] N. Shiguesada and K. Kawasaki, Biological Invasions: Theory and Practice, Oxford Series in Ecology and Evolution, 1990. [27] H. Thieme, Book review on Spatial Deterministic Epidemics by L. Rass and J. Radcliffe, AMS, 2003, Mathematical Biosciences, 2006, 202, 218–225. -
-
Figures(4)
Export File
Citation
Rehana Naz, Gangwei Wang, Saba Irum. THE CLOSED-FORM SOLUTIONS OF A DIFFUSIVE SUSCEPTIBLE-INFECTIOUS-SUSCEPTIBLE EPIDEMIC MODEL[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 574-586. doi: 10.11948/20240175
Format
Content
DownLoad:
-
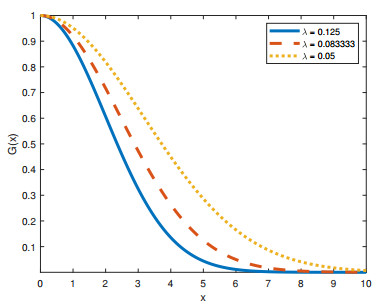
Figure 1.
The graphs of initial distribution of susceptible and infected individuals across the domain for different values of
$ \lambda=\frac{c_4 }{2c_2} $ $ 0\leq x\leq 10 $ -
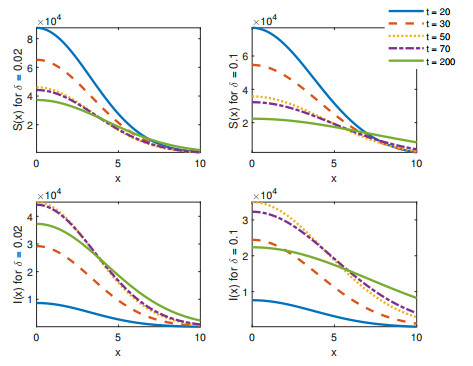
Figure 2.
Graphs of
$ S(x) $ $ I(x) $ $ \delta=0.02 $ $ \delta=0.1 $ $ c_2=10 $ $ c_4=1 $ $ \beta=0.4 $ $ \gamma=0.2 $ $ S_0=10^5-200 $ $ I_0=200 $ $ 0\leq x\leq 10 $ -
Figure 3.
Graphs of
$ S(t) $ $ I(t) $ $ \delta=0.02 $ $ \delta=0.1 $ $ c_2=10 $ $ c_4=1 $ $ \beta=0.4 $ $ \gamma=0.2 $ $ S_0=10^5-200 $ $ I_0=200 $ $ 0\leq t\leq 200 $ -
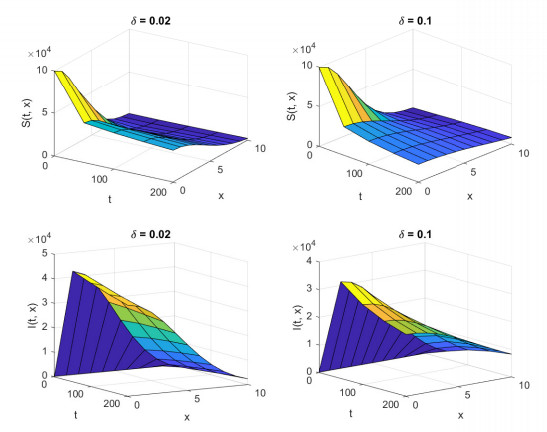
Figure 4.
Surface plots of
$ S $ $ I $ $ \delta=0.02 $ $ \delta=0.1 $ $ c_2=10 $ $ c_4=1 $ $ \beta=0.4 $ $ \gamma=0.2 $ $ S_0=10^5-200 $ $ I_0=200 $ $ 0\leq t\leq 200 $ $ 0\leq x\leq 10 $