| Citation: | Mine Aylin Bayrak, Ali Demir, Ahmet Büyük. A NOVEL ANALYTICAL METHOD FOR TIME FRACTIONAL CONVECTION-DIFFUSION EQUATION THROUGH CLIQUE POLYNOMIALS OF THE COCKTAIL PARTY GRAPH[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 564-573. doi: 10.11948/20240168 |
A NOVEL ANALYTICAL METHOD FOR TIME FRACTIONAL CONVECTION-DIFFUSION EQUATION THROUGH CLIQUE POLYNOMIALS OF THE COCKTAIL PARTY GRAPH
-
Abstract
This paper is devoted to providing a new approach to solve time fractional convection-diffusion equation (TFCDE) by utilizing Clique polynomials of the Cocktail party graph and collocation points. The main advantage of this method is converting the TFCDE into a system of ordinary fractional differential and algebraic equations. At this stage, Residual power series method (RPSM) is used to determine the unknown functions of the obtained system. Convergence analysis is given to substantiate the importance of the suggested method. Two numerical examples are presented to illustrate the implementation and effectiveness of the proposed method.
-

-
References
[1] R. Amin, B. Alshahrani, M. Mahmoud, A. H. Abdel-Aty, K. Shah and W. Deebani, Haar wavelet method for the solution of distributed order time-fractional differential equations, Alex. Eng. J., 2021, 60(3), 3295–3303. doi: 10.1016/j.aej.2021.01.039 [2] B. A. Carreras, V. E. Lynch and G. M. Zaslavsky, Anomalous diffusion and exit time distribution of particle tracers in plasma turbulence models, Phys. Plasmas., 2001, 8(12), 5096–5103. doi: 10.1063/1.1416180 [3] K. Diethelm, The Analysis of Fractional Differential Equations, Springer-Verlag, Berlin, 2010. [4] R. Hifler, Applications of Fractional Calculus in Physics, London, World Scientific Publishing Company, 2000. [5] M. Izadi, J. Singh and S. Noeiaghdam, Simulating accurate and effective solutions of some nonlinear nonlocal two-point BVPs: Clique and QLM-clique matrix methods, Heliyon, 2023, 9, e22267. doi: 10.1016/j.heliyon.2023.e22267 [6] M. M. Izadkhah and J. Saberi-Nadjafi, Gegenbauer spectral method for time-fractional convection-diffusion equations with variable coefficients, Math. Meth. Appl. Sci., 2015, 38(15), 3183–3194. doi: 10.1002/mma.3289 [7] A. Jajarmi, D. Baleanu, S. S. Sajjadi and J. J. Nieto, Analysis and some applications of a regularized ψ-Hilfer fractional derivative, J. Comput. Appl. Math., 2022, 415, 114476. doi: 10.1016/j.cam.2022.114476 [8] N. Jibenja, B. Yuttanan and M. Razzaghi, An efficient method for numerical solutions of distributed-order fractional differential equations, J. Comput. Nonlinear Dyn., 2018, 13(11), 111003. doi: 10.1115/1.4040951 [9] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and Applications of Fractional Differential Equations, in: North-Holland Mathematics Studies, Elsevier Science B.V., Amsterdam, 204, 2006. [10] V. S. S. Kumar, The Chebyshev collocation method for a class of time fractional convection-diffusion equation with variable coefficients, Math. Meth. Appl. Sci., 2021, 44, 6666–6678. doi: 10.1002/mma.7215 [11] O. Kurkcu, E. Aslan and M. Sezer, A novel graph-operational matrix method for solving multi delay fractional differential equations with variable coefficients and a numerical comparative survey of fractional derivative types, Turkish Journal of Mathematics, 2019, 43(1), 373–392. doi: 10.3906/mat-1806-87 [12] K. S. Miller and B. Ross, An Introduction to the Fractional Calculus and Fractional Differential Equations, Wiley, New York, 1993. [13] R. Metler and J. Klafter, The random walks guide to anomalous diffusion: A fractional dynamics approach, Phys. Reports, 2000, 339(1), 1–77. doi: 10.1016/S0370-1573(00)00070-3 [14] A. N. Nirmala and S. Kumbinarasaiah, A novel analytical method for the multi-delay fractional differential equations through the matrix of clique polynomials of the cocktail party graph, Results in Control and Optimization, 2023, 12, 100280. doi: 10.1016/j.rico.2023.100280 [15] A. N. Nirmala and S. Kumbinarasaiah, A new graph theoretic analytical method for nonlinear distributed order fractional ordinary differential equations by clique polynomial of cocktail party graph, Journal of Umm Al-Qura University for Applied Sciences, 2024. DOI: 10.1007/s43994-023-00116-8. [16] I. Podlubny, Fractional Differential Equations, Academic Press, San Diego, 1999 Physics and Engineering, Springer, Dordrecht, 2007. [17] M. Pourbabaee and A. Saadatmandi, Collocation method based on Chebyshev polynomials for solving distributed order fractional differential equations, Comput. Methods Differ. Equ., 2021, 9(3), 858–873. [18] M. Raberto, E. Scalas and F. Mainardi, Waiting-times and returns in high-frequency financial data: An empirical study, Phys. A: Stat. Mech. Appl., 2002, 314(1–4), 749–755. doi: 10.1016/S0378-4371(02)01048-8 [19] M. Randic, P. J. Hansen and P. C. Jurs, Search for useful graph theoretical invariants of molecular structure, J. Chem. Inf. Comput. Sci., 1988, 28(2), 60–68. doi: 10.1021/ci00058a004 [20] A. Saadatmandi, M. Dehghan and M. R. Azizi, The Sinc-Legendre collocation method for a class of fractional convection-diffusion equations with variable coefficients, Commun. Nonlinear Sci. Numer. Simul., 2012, 17(11), 4125–4136. doi: 10.1016/j.cnsns.2012.03.003 [21] L. Sabatelli, S. Keating, J. Dudley and P. Richmond, Waiting time distributions in financial markets, Eur. Phys. J. B., 2002, 27(2), 273–275. [22] Y. Shi, M. Dehmer, X. Li and I. Gutman(eds), Graph Polynomials, CRC Press (List of graph polynomials), 2016. [23] H. Sun, Y. Zhang, D. Baleanu, W. Chen and Y. Chen, A new collection of real-world applications of fractional calculus in science and engineering, Commun. in Nonlin. Sci. Num. Simul., 2018, 64, 213–231. doi: 10.1016/j.cnsns.2018.04.019 [24] G. S. Teodoro, J. T. Machado and E. C. De Oliveira, A review of definitions of fractional derivatives and other operators, J. Comput. Phys., 2019, 388, 195–208. doi: 10.1016/j.jcp.2019.03.008 [25] H. Wang, K. Wang and T. Sircar, A direct O(N log2 N) finite difference method for fractional diffusion equations, J. Comput. Phys., 2010, 229(21), 8095–8104. doi: 10.1016/j.jcp.2010.07.011 [26] K. Wang and H. Wang, A fast characteristic finite difference method for fractional advection-diffusion equations, Adv. Water Res., 2011, 34(7), 810–816. doi: 10.1016/j.advwatres.2010.11.003 [27] Y. Xu, Y. Zhang and J. Zhao, Error analysis of the Legendre-Gauss collocation methods for the nonlinear distributed-order fractional differential equation, Appl. Numer. Math., 2019, 142, 122–138. doi: 10.1016/j.apnum.2019.03.005 [28] G. M. Zaslavsky, D. Stevens and H. Weitzner, Self-similar transport in incomplete chaos, Phys. Rev. E, 1993, 48(3), 1683–1694. doi: 10.1103/PhysRevE.48.1683 [29] J. Zhang, X. Zhang and B. Yang, An approximation scheme for the time fractional convection-diffusion equation, Appl. Math. Comput., 2018, 335, 305–312. -
-
-
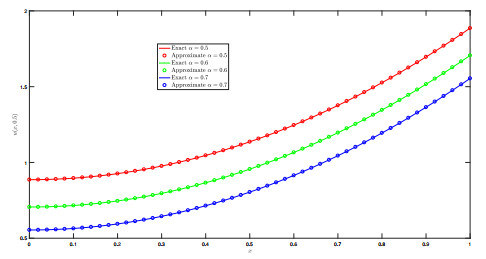
Figure 1.
The graph of exact and numerical solution for various
$ \alpha $ $ m=3 $ $ T=0.1 $ -
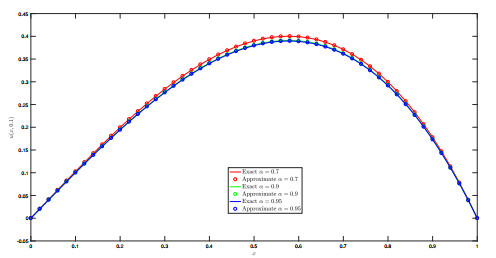
Figure 2.
The graph of numerical and exact solution for
$ \alpha=0.5 $ $ T=0.5 $




 DownLoad:
DownLoad: