| Citation: |
Hammed Anuoluwapo Abass, Olawale Kazeem Oyewole. A PARALLEL TSENG’S SPLITTING METHOD FOR COMMON SOLUTION OF VARIATIONAL INCLUSIONS AND FIXED POINT PROBLEMS ON HADAMARD MANIFOLDS[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 839-861. doi: 10.11948/20240176
|
A PARALLEL TSENG’S SPLITTING METHOD FOR COMMON SOLUTION OF VARIATIONAL INCLUSIONS AND FIXED POINT PROBLEMS ON HADAMARD MANIFOLDS
-
Abstract
In this manuscript, we propose an inertial forward-backward-forward splitting method for common solution of variational inclusions and fixed point problems of nonexpansive mappings in the framework of a Hadamard manifold. Using our iterative method together with a self-adaptive method which generates dynamic step-size converging to a positive constant, we establish that the sequence generated by our method converges to a common solution of variational inclusions and fixed point problems. Also, we illustrate a numerical example to show the performance of our method. The result discuss in this article extends and complements many related results in the literature.
-
-
References
[1] H. A. Abass, Halpern inertial subgradient extragradient algorithm for solving equilibrium problems in Banach spaces, Applicable Analysis, 2024. DOI: 10.1080/00036811.2024.2360507. [2] H. A. Abass, G. C. Godwin, O. K. Narain and V. Darvish, Inertial extragradient method for solving variational inequality and fixed point problems of a bregman demigeneralized mapping in a reflexive banach spaces, Numer. Funct. Anal. and Optim., 2022, 43(8), 933-960. doi: 10.1080/01630563.2022.2069813 [3] H. A. Abass, O. K. Oyewole, K. O. Aremu and L. O. Jolaoso, Modified inertial Tseng method for solving variational inclusion and fixed point problems on Hadamard manifolds, Applicable Analysis, 2023, 1-24. [4] H. A. Abass, O. K. Oyewole and L. O. Jolaoso, Self adaptive technique with double inertial steps for inclusion problem on Hadamard manifolds, J. Oper. Res. Soc., 2024. DOI: 10.1007/s40305-024-00537-0. [5] F. Alvarez and H. Attouch, An inertial proximal method for maximal monotone operators via discretization of a nonlinear oscillator with damping, Set-Valued Anal., 9 (2001), 3-11. doi: 10.1023/A:1011253113155 [6] A. Beck and M. Teboulle, A fast iterative shrinkage-thresholding algorithm for linear inverse problem, SIAM J. Imaging Sci., 2009, 2, 183-202. doi: 10.1137/080716542 [7] M. R. Bridson and A. Haefliger, Metric Spaces of Non-Positive Curvature. Grundlehren der Mathematischen Wissenschaften (Fundamental Principles of Mathematical Sciences), 319, Springer, Berlin, 1999. DOI: 10.1007/978-3-662-12494-9. [8] F. E. Browder, Existence and approximation of solutions of nonlinear variational inequalities, Proc. Net. Acod. Sci. USA, 1966, 56, 1080-1086. doi: 10.1073/pnas.56.4.1080 [9] P. Chaipunya, K. Khammahawong and P. Kumam, Iterative algorithm for singularities of inclusion problem in Hadamard manifolds, J. Inequal. Appl., 2021, 2021, 147. doi: 10.1186/s13660-021-02676-x [10] L. Ciric, S. Jesic, M. M. Milavanovic and J. S. Ume, On the sterpest decent approximation method for the zeros of generalized accretive operators, Nonlinear Anal., 2008, 69, 763-769. doi: 10.1016/j.na.2007.06.021 [11] J. X. Cruz, O. P. Ferreira, L. R. Pérez, et al., Monotone point-to-set vector fields, Balkan J. Geom. Appl., 2000, 5(1), 69-79. [12] I. Daubechies, M. Defrise and C. De Mol, An iterative thresholding algorithm for linear inverse problems with a sparsity constraints, Commun. Pure Appl. Math., 2004, 57, 1413-1457. doi: 10.1002/cpa.20042 [13] M. Dilshad, A. Khan and M. Akram, Splitting type viscosity methods for inclusion and fixed point problems on Hadamard manifold, AIMS Math., 2021, 6(5), 5205-5221. doi: 10.3934/math.2021309 [14] O. P. Ferreira and P. R. Oliveira, Proximal point algorithm on Riemannian manifolds, Optimization, 2002, 51(2), 257-270. doi: 10.1080/02331930290019413 [15] D. Filali, M. Dilshad, M. Akram, F. Babu and I. Ahmad, Viscosity method for hierachical variational inequalities and variational inclusions on Hadamard manifold, J. Inequal. Appl., 2021, 2021, 1-20. doi: 10.1186/s13660-020-02526-2 [16] A. Gibali and D. V. Thong, Tseng type methods for solving inclusion problems and its application, Calcolo, 2018, 55, 49. doi: 10.1007/s10092-018-0292-1 [17] N. Gupta, S. Haseen and A. Bari, Reliability optimization problems with multiple constraints under fuzziness, J. Ind. Eng. Int., 2016, 12, 459-467. doi: 10.1007/s40092-016-0157-7 [18] K. Khammahawong, P. Chaipunya and P. Kumam, An inertial Mann algorithm for nonexpansive for nonexpansive mappings on Hadamard manifolds, AIMS Mathematics, 2023, 8(1), 2093-2116. [19] K. Khammahawong, P. Kumam, P. Chaipunya and J. M. Martinez, Tseng's method for inclusion problems on Hadamard manifolds, Optimization, 2022, 71(15), 4367-4401. doi: 10.1080/02331934.2021.1940179 [20] C. Li, G. López and V. Martín-Márquez, Monotone vector fields and the proximal point algorithm on Hadamard manifolds, J. Lond. Math. Soc., 2009, 79(3), 663-683. DOI: 10.1112/jlms/jdn087. [21] P. L. Lions and B. Mercier, Splitting algorithm for the sum of nonlinear operators, SIAM J. Numer. Anal., 1979, 16, 964-979. doi: 10.1137/0716071 [22] P. E. Maingé, Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization, Set-Valued Anal., 2008, 16, 899-912. doi: 10.1007/s11228-008-0102-z [23] T. Mouletonglang, K. Poochinapan and R. Suparatulatorn, A parallel method for common variational inclusion and common fixed point problem with application, carpathian, J. Math., 2023, 39(1), 189-200. [24] O. K. Oyewole and S. Reich, An inertial subgradient extragradient method for approximating solution to equilibrium problems in Hadamard manifold, Axioms., 2023, 12, 256. doi: 10.3390/axioms12030256 [25] B. T. Polyak, Some methods of speeding up the convergence of iterarive methods, Zh. Vychisl. Mat. Mat. Fiz., 4, 1964, 1-17. [26] R. T. Rockafellar, Monotone operators and the proximal point algorithm, SIAM J. Control Optim., 1976, 14(5), 877-898. doi: 10.1137/0314056 [27] T. Sakai, Riemannian Geometry, Vol. 149, Translations of Mathematical Monographs, Providence (RI): American Mathematical Society; 1996. Translated from the 1992 Japanese original by the author. [28] S. Suanta, K. Kankam and W. Cholamjiak, A parallel monotone hybrid algorithm for a finite of G-nonexpanaive mappings in Hilbert spaces endowed with a graph applicable in signal recovery, Comp. Appl. Math., 2021, 40, article No. 145. doi: 10.1007/s40314-021-01530-6 [29] R. Suparatulorn, W. Cholamjiak, A. Gibali and T. Mouktonglang, A parallel Tseng's splitting method for solving common variational inclusion applied to signal recovery problems, Adv. Differ. Eqiu., 2021, 2021, article No. 4. doi: 10.1186/s13662-020-03178-8 [30] S. Takahashi, W Takahashi amd M. Toyoda, Strong converge theorems for maximal monotone operators with nonlinear mappings in Hilbert spaces, J. Optim. Theory Appl., 2010, 147, 27-41. doi: 10.1007/s10957-010-9713-2 [31] P. A. Tseng, A modified forward-backward splitting method for maximal monotone mappings, SIAM J. Control Optim., 2009, 38, 431-446. [32] J. H. Wang, G. López, V. Martín-Márquez and C. Li, Monotone and accretive vector fields on Riemannian manifolds, J. Optim Theory Appl., 2010, 146, 691-708. doi: 10.1007/s10957-010-9688-z [33] H. K. Xu, An iterative approach to quadratic optimization, J. Optim. Theory Appl., 2003, 116, 659-678. DOI: 10.1023/A:1023073621589. -
-
Figures(1)
Export File
Citation
Hammed Anuoluwapo Abass, Olawale Kazeem Oyewole. A PARALLEL TSENG’S SPLITTING METHOD FOR COMMON SOLUTION OF VARIATIONAL INCLUSIONS AND FIXED POINT PROBLEMS ON HADAMARD MANIFOLDS[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 839-861. doi: 10.11948/20240176
Format
Content
DownLoad:
-
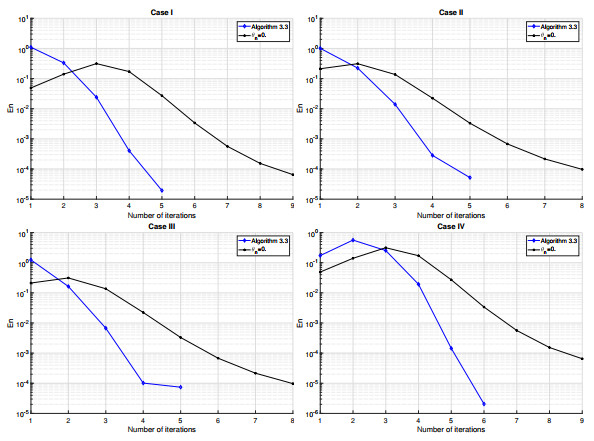
Figure 1.
Example 4. Top Left: Case 1, Top Right: Case 2, Bottom right: Case 3, Bottom left: Case 4