| Citation: |
Manpal Singh, S. Das, Rajeev, E. M. Craciun. NUMERICAL SIMULATION OF VARIABLE ORDER FRACTIONAL COUPLED FITZHUGH-NAGUMO REACTION-DIFFUSION PROBLEM AND IT'S ANALYSIS[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 810-838. doi: 10.11948/20240164
|
NUMERICAL SIMULATION OF VARIABLE ORDER FRACTIONAL COUPLED FITZHUGH-NAGUMO REACTION-DIFFUSION PROBLEM AND IT'S ANALYSIS
-
Abstract
A novel scheme for numerical simulation of the variable order fractional partial differential equation (VOFPDE) has been presented in this article, which has been applied to find the approximate solution of the variable order time fractional coupled Fitzhugh-Nagumo reaction-diffusion equation. The solution of the considered model exists and is unique, and the aforementioned model will remain stable under the Ulam-Hyers test. It has been found that Vieta-Fibonacci wavelets are the appropriate basis function to solve the aforementioned problem numerically, and the operational matrices of the Vieta-Fibonacci wavelets have been derived for both integer as well as variable order fractional derivatives. Using these derived operational matrices and properties of Vieta-Fibonacci wavelets combined with the collocation method, the main problem is reduced to an algebraic system of equations, which has been solved easily. The salient feature of the article is the convergence analysis of the proposed method, which is discussed. The error analysis between the approximate solution of the particular cases of the concerned model using the proposed technique and their exact solutions has been presented through tables and figures.
-
-
References
[1] W. Abd-Elhameed, E. Doha and Y. Youssri, New spectral second kind Chebyshev wavelets algorithm for solving linear and nonlinear second-order differential equations involving singular and Bratu type equations, Abstract and Applied Analysis, 2013, 2013(1). DOI: 10.1155/2013/715756. [2] P. Agarwal, A. El-Sayed and J. Tariboon, Vieta–Fibonacci operational matrices for spectral solutions of variable-order fractional integro-differential equations, Journal of Computational and Applied Mathematics, 2021, 382, 113063. DOI: 10.1016/j.cam.2020.113063. [3] R. Amin, K. Shah, M. Asif, I. Khan and F. Ullah, An efficient algorithm for numerical solution of fractional integro-differential equations via Haar wavelet, Journal of Computational and Applied Mathematics, 2021, 381, 113028. DOI: 10.1016/j.cam.2020.113028. [4] Anjuman, A. Y. Leung and S. Das, Two–dimensional time–fractional nonlinear drift reaction–diffusion equation arising in electrical field, Fractal and Fractional, 2024, 8(8), 456. DOI: 10.3390/fractalfract8080456. [5] H. Azin, M. H. Heydari and F. Mohammadi, Vieta–Fibonacci wavelets: Application in solving fractional pantograph equations, Mathematical Methods in the Applied Sciences, 2022, 45(1), 411–422. doi: 10.1002/mma.7783 [6] Y. Chen, Y. Sun and L. Liu, Numerical solution of fractional partial differential equations with variable coefficients using generalized fractional-order Legendre functions, Applied Mathematics and Computation, 2014, 244, 847–858. doi: 10.1016/j.amc.2014.07.050 [7] D. Chouhan, V. Mishra and H. Srivastava, Bernoulli wavelet method for numerical solution of anomalous infiltration and diffusion modeling by nonlinear fractional differential equations of variable order, Results in Applied Mathematics, 2021, 10, 100146. DOI: 10.1016/j.rinam.2021.100146. [8] E. Craciun and M. Singh, Operational matrix method to solve nonlinear reaction-advectiondiffusion equation in fractional order system, Analele ştiinţifice ale Universităţii "Ovidius" Constanţa Seria Matematică, 2022, 30(3), 97–116. [9] S. Das, Analytical solution of a fractional diffusion equation by variational iteration method, Computers & Mathematics with Applications, 2009, 57(3), 483–487. [10] S. Das, A note on fractional diffusion equations, Chaos, Solitons & Fractals, 2009, 42(4), 2074–2079. [11] M. Derakhshan, Existence, uniqueness, Ulam–Hyers stability and numerical simulation of solutions for variable order fractional differential equations in fluid mechanics, Journal of Applied Mathematics and Computing, 2022, 68(1), 403–429. doi: 10.1007/s12190-021-01537-6 [12] U. Farooq, H. Khan, D. Baleanu and M. Arif, Numerical solutions of fractional delay differential equations using Chebyshev wavelet method, Computational and Applied Mathematics, 2019, 38, 1–13. [13] B. Ghanbari and S. Kumar, A study on fractional predator–prey–pathogen model with Mittag–Leffler kernel-based operators, Numerical Methods for Partial Differential Equations, 2024, 40(1), e22689. DOI: 10.1002/num.22689. [14] M. Heydari and Z. Avazzadeh, A new wavelet method for variable–order fractional optimal control problems, Asian Journal of Control, 2018, 20(5), 1804–1817. doi: 10.1002/asjc.1687 [15] M. Heydari, Z. Avazzadeh and A. Atangana, Shifted Vieta–Fibonacci polynomials for the fractalfractional fifth–order Kdv equation, Mathematical Methods in the Applied Sciences, 2021, 44(8), 6716–6730. doi: 10.1002/mma.7219 [16] L. Hou, H. Kokubu, A. Marciniak-Czochra and I. Takagi, Existence of traveling wave solutions to reaction–diffusion–ODE systems with hysteresis, Journal of Differential Equations, 2023, 364, 667–713. doi: 10.1016/j.jde.2023.04.032 [17] A. Jajarmi and D. Baleanu, A new iterative method for the numerical solution of high–order non–linear fractional boundary value problems, Journal of Differential Equations, 2020, 8, 220. DOI: 10.3389/fphy.2020.00220. [18] M. Javidi and B. Ahmad, Numerical solution of fractional partial differential equations by numerical Laplace inversion technique, Advances in Difference Equations, 2013, 2013(1), 1–18. doi: 10.1186/1687-1847-2013-1 [19] M. Kashif, M. Singh, T. Som and E.-M. Craciun, Numerical study of variable order model arising in chemical processes using operational matrix and collocation method, Journal of Computational Science, 2024, 80, 102339. DOI: 10.1016/j.jocs.2024.102339. [20] D. Kumar, J. Singh, D. Baleanu and Sushila, Analysis of regularized long–wave equation associated with a new fractional operator with Mittag–Leffler type kernel, Physica A: Statistical Mechanics and its Applications, 2018, 492, 155–167. doi: 10.1016/j.physa.2017.10.002 [21] S. Kumar, R. Chauhan, S. Momani and S. Hadid, Numerical investigations on COVID-19 model through singular and non–singular fractional operators, Numerical Methods for Partial Differential Equations, 2024, 40(1), e22707. DOI: 10.1002/num.22707. [22] S. Kumar, R. Kumar, M. Osman and B. Samet, A wavelet based numerical scheme for fractional order SEIR epidemic of measles by using Genocchi polynomials, Numerical Methods for Partial Differential Equations, 2021, 37(2), 1250–1268. doi: 10.1002/num.22577 [23] S. Kumar, A. Kumar, B. Samet and H. Dutta, A study on fractional host–parasitoid population dynamical model to describe insect species, Numerical Methods for Partial Differential Equations, 2021, 37(2), 1673–1692. doi: 10.1002/num.22603 [24] S. Kumar, P. Pandey and S. Das, Gegenbauer wavelet operational matrix method for solving variable–order non–linear reaction–diffusion and Galilei invariant advection–diffusion equations, Computational and Applied Mathematics, 2019, 38, 1–22. [25] A. Mahmoud, I. G. Ameen and A. A. Mohamed, A new operational matrix based on Jacobi wavelets for a class of variable–order fractional differential equations, Proceedings of the Romanian Academy Series A, 2017, 18(4), 315–322. [26] F. Mohammadi and M. Hosseini, A new Legendre wavelet operational matrix of derivative and its applications in solving the singular ordinary differential equations, Journal of the Franklin Institute, 2011, 348(8), 1787–1796. doi: 10.1016/j.jfranklin.2011.04.017 [27] S. Qureshi and A. Atangana, Mathematical analysis of dengue fever outbreak by novel fractional operators with field data, Physica A: Statistical Mechanics and its Applications, 2019, 526, 121127. DOI: 10.1016/j.physa.2019.121127. [28] H. Saeedi, M. M. Moghadam, N. Mollahasani and G. Chuev, A CAS wavelet method for solving nonlinear Fredholm integro–differential equations of fractional order, Communications in Nonlinear Science and Numerical Simulation, 2011, 16(3), 1154–1163. doi: 10.1016/j.cnsns.2010.05.036 [29] K. Shah, M. A. Alqudah, F. Jarad and T. Abdeljawad, Semi–analytical study of PineWilt Disease model with convex rate under Caputo–Febrizio fractional order derivative, Chaos, Solitons & Fractals, 2020, 135, 109754. DOI: 10.1016/j.chaos.2020.109754. [30] J. Singh, D. Kumar, Z. Hammouch and A. Atangana, A fractional epidemiological model for computer viruses pertaining to a new fractional derivative, Applied mathematics and computation, 2018, 316, 504–515. doi: 10.1016/j.amc.2017.08.048 [31] M. Singh, S. Das, Rajeev and E. Craciun, Numerical solution of two–dimensional nonlinear fractional order reaction–advection–diffusion equation by using collocation method, Analele ştiinţifice ale Universităţii "Ovidius" Constanţa Seria Matematică, 2021, 29(2), 211–230. doi: 10.2478/auom-2021-0027 [32] S. Sohrabi, Comparison Chebyshev wavelets method with BPFs method for solving Abel's integral equation, Ain Shams Engineering Journal, 2011, 2(3–4), 249–254. [33] J. Solís-Pérez, J. Gómez-Aguilar and A. Atangana, Novel numerical method for solving variable order fractional differential equations with power, exponential and Mittag–Leffler laws, Chaos, Solitons & Fractals, 2018, 114, 175–185. [34] H. Srivastava, F. Shah and R. Abass, An application of the Gegenbauer wavelet method for the numerical solution of the fractional Bagley–Torvik equation, Russian Journal of Mathematical Physics, 2019, 26(1), 77–93. doi: 10.1134/S1061920819010096 [35] P. T. Toan, T. N. Vo and M. Razzaghi, Taylor wavelet method for fractional delay differential equations, Engineering with Computers, 2021, 37, 231–240. [36] P. Veeresha, D. Prakasha and S. Kumar, A fractional model for propagation of classical optical solitons by using nonsingular derivative, Mathematical Methods in the Applied Sciences, 2024, 47, 10609–10623. [37] F. Yousefi, A. Rivaz and W. Chen, The construction of operational matrix of fractional integration for solving fractional differential and integro–differential equations, Neural Computing and Applications, 2019, 31, 1867–1878. [38] B. Yuttanan and M. Razzaghi, Legendre wavelets approach for numerical solutions of distributed order fractional differential equations, Applied Mathematical Modelling, 2019, 70, 350–364. [39] Q. Zheng and J. Shen, Pattern formation in the FitzHugh–Nagumo model, Computers & Mathematics with Applications, 2015, 70(5), 1082–1097. -
-
Figures(4) / Tables(2)
Export File
Citation
Manpal Singh, S. Das, Rajeev, E. M. Craciun. NUMERICAL SIMULATION OF VARIABLE ORDER FRACTIONAL COUPLED FITZHUGH-NAGUMO REACTION-DIFFUSION PROBLEM AND IT'S ANALYSIS[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 810-838. doi: 10.11948/20240164
Format
Content
DownLoad:
-
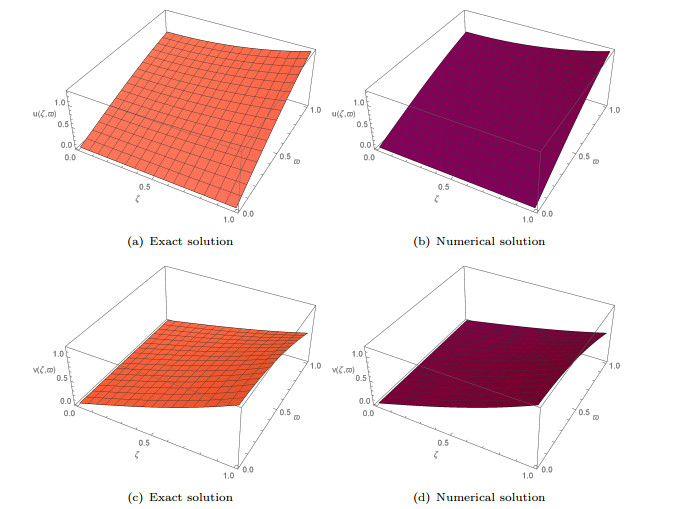
Figure 1.
Behaviour of exact solution and their corresponding numerical solutions for Example 8.1 at
$ \hat{m}=4 $ -
Figure 2.
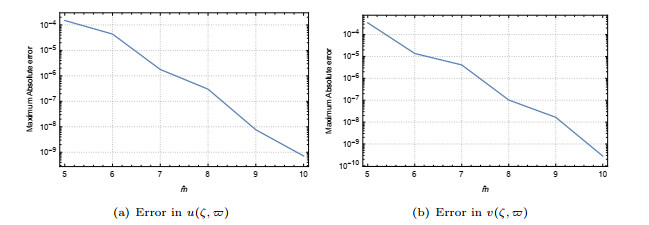
Comparison of maximum absolute error for Example 8.1 for different value of
$ \hat{m} $ $ \varpi=0.5 $ -
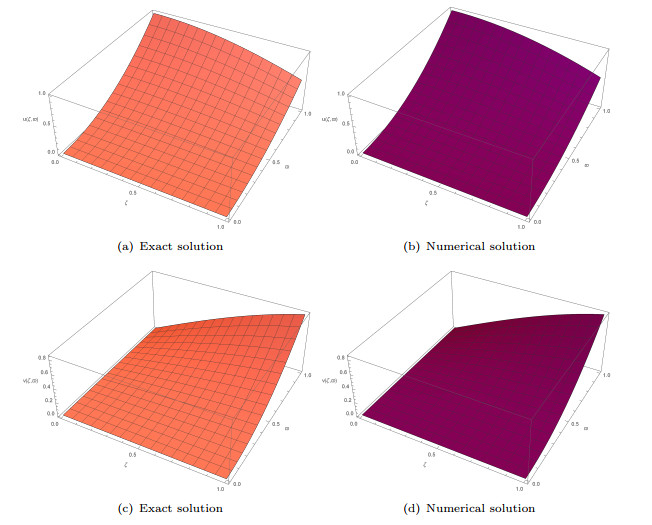
Figure 3.
Behaviour of exact solution and their corresponding numerical solutions for Example 8.2 at
$ \hat{m}=10 $ -
Figure 4.
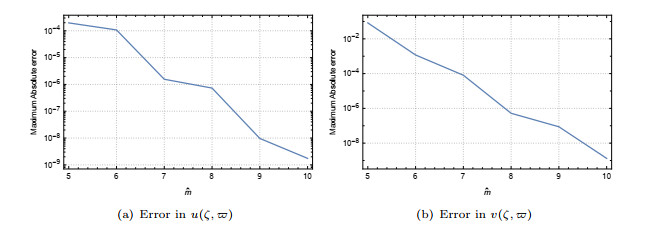
Comparison of maximum absolute error for Example 8.2 for different value of
$ \hat{m} $ $ \varpi=0.5 $