| Citation: | Pius W. M. Chin. THE EXISTENCE OF THE GLOBAL SOLUTION OF THE SEMI-LINEAR SCHRÖDINGER EQUATION WITH NUMERICAL COMPUTATION ON THE DIRICHLET BOUNDARY[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 786-809. doi: 10.11948/20240161 |
THE EXISTENCE OF THE GLOBAL SOLUTION OF THE SEMI-LINEAR SCHRÖDINGER EQUATION WITH NUMERICAL COMPUTATION ON THE DIRICHLET BOUNDARY
-
Abstract
This paper concerns the analysis of the initial boundary value problem for the semi-linear Schrödinger equation. In the paper, we design a reliable scheme coupling the nonstandard finite difference method in time with the Galerkin combined with the compactness method in the space variables to analyze the problem. The analysis begins by showing that, given initial solutions in specified space, the global solution of the Schrödinger equation exists uniquely. We further show using the a priori estimates obtained from the existence process, that the numerical solution from the designed scheme is stable and converges optimally in specified norms. Furthermore, we show that the scheme replicates or preserves the qualitative properties of the exact solution. Numerical experiments are conducted using a carefully chosen example to justify our theoretical proposition.
-

-
References
[1] A. R. Adams, Sobolev Space, Academic Press, New York, 1975. [2] A. A. Aderogba and A. R. Appadu, Classical and multisymplectic schemes for linearized KdV equation: Numerical results and dispersion analysis, Fluids, 2021, 6, 214. https://doi.org/10.3390/fluids/6060214. doi: 10.3390/fluids/6060214 [3] A. M. Agbavon, A. R. Appadu and M. Khumalo, On the numerical solution of Fisher's equation with coefficient of diffusion term much smaller than coefficient of reaction term, Adv. Differ. Equ., 2019, 146(2019). https://doi.org/10.1186/s13662-019-2080-x. doi: 10.1186/s13662-019-2080-x [4] R. Anguelov and J. M.-S. Lubuma, Contributions to the mathematics of the nonstandard finite difference method and applications, Numerical Methods for Partial Differential Equations, 2001, 17(5), 518–543. doi: 10.1002/num.1025 [5] R. Anguelov and J. M.-S. Lubuma, Nonstandard finite difference method by nonlocal approximation, Mathematics and Computers in Simulation, 2003, 61(3), 465–475. [6] A. R. Appadu and A. S. Kelil, Comparison of modified ADM and classical finite difference method for some third-order and fifth-order KdV equations, Demonstratio Mathematica, 2021, 54, 377–409. https://doi.org/10.1515/dema-2021-0039. doi: 10.1515/dema-2021-0039 [7] A. R. Appadu and A. S. Kelil, Some finite difference methods for solving linear fractional KdV equation, Front. Appl. Math. Stat., 2023, 9, 1261270. https://doi.org/10.3389/fams.2023.1261270. doi: 10.3389/fams.2023.1261270 [8] J. P. Aubin, Un théoréme de compacité, C. R. Acad. Sc. Paris, 1963, 256, 5012–5014. [9] H. P. Bhatt and A. Q. M. Khaliq, Higher order exponential time differencing scheme for system of coupled nonlinear Schrödinger equations, Appl. Math. Comput., 2014, 228, 271–291. [10] A. Biswas, Soliton solutions of the perturbed resonant nonlinear Schrödinger's equation with full nonlinearity by semi-inverse variational principle, Quant. Phys. Lett., 2012, 1(2), 79–86. [11] H. Brezis and T. Gallouet, Nonlinear Schrodinger evolution equations, Nonlinear Analysis, 1980, 4, 677–681. doi: 10.1016/0362-546X(80)90068-1 [12] C. Bu, Nonlinear Schrödinger equation on the semi-infinite line, Chinese Annals of Math., 2000, 21A, 1–12. [13] J. Cai, Y. Wang and H. Liang, Local energy-preserving and momentum-preserving algorithms for coupled nonlinear Schrödinger system, J. Comput. Phys., 2013, 239, 30–50. [14] B. Carroll and C. Bu, Solution of the forced nonlinear Schrödinger equation (NLS) using PDE techniques, Appl. Anal., 1991, 41, 33–51. [15] Y. Chen, H. Zhu and S. Song, Multi-symplectic splitting method for the coupled nonlinear Schrödinger system, Comput. Phys. Comm., 2010, 181(7), 1231–1241. [16] P. W. M. Chin, The Galerkin reliable scheme for the numerical analysis of the Burgers'-Fisher equation, Progress in Computational Fluid Dynamics, 2021, 21(4), 234–247. [17] P. W. M. Chin, The analysis of an efficient numerical scheme for the Allen-Cahn equations using the Galerkin method, Communications in Nonlinear Science and Numerical Simulation, 2022, 105, 106061. [18] P. W. M. Chin, The analysis of the solution of the Burgers-Huxley equation using the Galerkin method, Numerical Methods of Partial Differential Equations, 2023, 39(4), 2787–2807. [19] P. W. M. Chin, The effect on the solution of the Fitzhugh-Nagumo equation by the external parameter $\alpha$ using the Galerkin method, Journal of Applied Analysis and Computation, 2023, 13(4), 1983–2005. $\alpha$ using the Galerkin method" target="_blank">Google Scholar
[20] P. Q. Ciarlet, The Finite Element Method for Elliptic Problems, Elsevier, North Holland, 1978. [21] L. C. Evan, Partial Differential Equations, Graduate, Studies in Mathematics, volume 19, American Mathematical Society, Rhode Island, 1998. [22] D. C. R. Gomes, M. A. Rincon, M. D. G. da Silva and G. O. Antunes, Numerical and mathematical analysis of a nonlinear Schrödinger problem with moving ends, Journal of Applied Analysis and Computation, 2024, 14(2), 886–910. DOI: 10.11948/20230189. [23] H. Hashimoto and H. Ono Nonlinear modulations of gravity waves, J. Phys. Soc. Jpn., 1972, 33, 805–811. [24] X. Hu and L. Zhang, Conservative compact difference schemes for the coupled nonlinear Schrödinger system, Numer. Methods Partial Differential Equations, 2014, 30(3), 749–772. [25] L. Huang and J. Su, Multiple solutions for nonhomogeneous quasilinear Schrödinger-Poisson system, Journal of Applied Analysis and Computation, 2023, 13(8), 1597–1612. doi: 10.11948/20220404 [26] M. S. Ismail and T. R. Taha, A linearly implicit conservative scheme for the coupled nonlinear Schrödinger equation, Math. Comput. Simulation, 2007, 74(4–5), 302–311. [27] P. L. Kelley, Self-focusing of optical beams, Physical, Review Letter, 1965, 15, 1005–1008. [28] L. Kong, J. Hong, L. Ji and P. Zhu, Compact and efficient conservative scheme for coupled nonlinear Schrödinger equation, Numer. Methods Partial Differential Equations, 2015, 31(6), 1814–1843. [29] O. A. Ladyzhenskaya, The Boundary Value Problems of Mathematical Physics, Springer-Verlag, New York, 1985, 322p. [30] A. Li, C. Wei and L. Zhao, Nontrivial generalized solution of Schrödinger-poisson system $\mathbb{R}^{3}$ with zero mass and periodic potential, Journal of Applied Analysis and Computations, 2023, 13(6), 3491–3503. DOI: 10.11948/20230122. CrossRef $\mathbb{R}^{3}$ with zero mass and periodic potential" target="_blank">Google Scholar
[31] L. Liu, H. Chen and J. Yang, Decay properties and asymptotic behavior of positive solutions for the nonlinear fractional Schrödinger-Poisson system, Journal of Applied Analysis and Computational, 2023, 13(6), 3136–3157. DOI: 10.11948/20220378. [32] J.-L. Louis, E. Magenes and P. Kenneth, Non-Homogeneous Boundary Value Problems and Applications, Volume 1, Springer Berlin, 1972. [33] Y. Ma, L. Kong, J. Hong and Y. Cao, Higher-order compact splitting multisymplectic method for the coupled nonlinear Schrödinger equations, Comput. Math. Appl., 2011, 61(2), 319–333. [34] R. E. Mickens, Nonstandard Finite Difference Models of Differential Equations, World Scientific Publishing, River Edge NJ, USA, 1994. [35] K. C. Partidar, On the use of nonstandard finite difference methods, Journal of Difference Equations and Applications, 2005, 11(8), 735–758. [36] W. Rudin, Functional Analysis. McGraw-Hill, New York, 1991. [37] K. Schimizu and Y. H. Ichikawa, Automodulation of ion oscillation modes in plasma, J. Phys. Soc. Jpn., 1972, 33, 789–792. [38] J. Shen, Long time stability and convergence for the fully discrete nonlinear Galerkin methods, Appl. Anal., 1990, 38, 201–229. [39] W. J. Sonnier and C. I. Christov, Strong coupling of Schrödinger equations: Condservative scheme approach, Math. Comput. Simulation, 2005, 69(5–6), 514–525. [40] K. Stewartson and J. T. Stuart, A nonlinear instability theory for a wave system in plane poiseuille flow, J. of Fluid Mechanic, 1971, 48(3), 529–545. [41] C. Sulem and P.-L. Sulem, The Nonlinear Schrödinger Equation, Applied Mathematical Sciences, 139, Springer-Verlag, New York, 1999. [42] V. I. Talanov, Self-focusing of wave beams in nonlinear media, Soviet Physics, JETP Letters, 1965, 2, 138–141. [43] R. Temam, Navier-Stokes Equations: Theory and Numerical Analysis, Amsterdam, North-Holland, 1984. [44] R. Temam, Infinite Dimensional Dynamical System in Mechanics and Physics, Springer-Verlag, New York, 1997. [45] H. Triki, T. Hayat, O. M. Aldossary and A. Biswas, Bright and dark solitons for the resonant nonlinear Schrödinger equation with time-dependent coefficients, Optics. and Laser Tecnology, 2012, 44(7), 2223–2231. [46] M. Tsutsumi, On smooth solutions to the initial-boundary value problem for the nonlinear Schrödinger equations in two space dimension, Nonlinear Anal., 1989, 13, 1051–1056. [47] M. Tsutsumi, On global solutions to the initial-boundary value problem for the nonlinear Schrödinger equations in exterior domain, Comm. Partial Differential Equations, 1991, 16, 885–907. [48] Y. Tsutsumi, Global solutions of the nonlinear Schrödinger equations in exterior domain, Comm. Partial Differential Equations, 1983, 8, 1337–1374. [49] T. Wang, Maximum norm error band of a linearised difference scheme for a coupled nonlinear Schrödinger equations, J. Comput. Appl. Math., 2011, 235(14), 4237–4250. [50] A.-M. Wazwaz, Exact solutions for the fourth order nonlinear Schrödinger equations with cubic and power law nonlinearities, Math. Comput. Modelling, 2006, 43(7–8), 802–808. [51] M. F. Wheeler, A priori $L^{2}$ error estimates for Galerkin approximations to parabolic partial differential equations, SIAM J. Numer. Anal., 1973, 10, 723–759. -
-
-
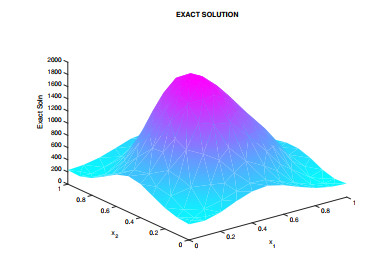
Figure 1.
The Exact Computed Solution
-
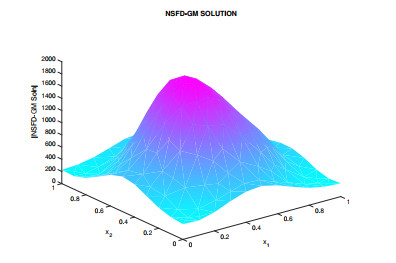
Figure 2.
Approximate solution for NSFD-GM Scheme
-
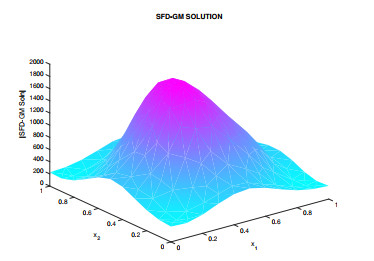
Figure 3.
Approximate solution for SFD-GM Scheme




 DownLoad:
DownLoad: