| Citation: | Imran Ali, Mohd Ishtyak, Javid Iqbal, Yuanheng Wang, Rais Ahmad. INERTIAL EXTRAPOLATION SCHEME FOR SYSTEM OF VARIATIONAL INCLUSIONS USING GENERALIZED YOSIDA AND CAYLEY OPERATORS[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1398-1412. doi: 10.11948/20240232 |
INERTIAL EXTRAPOLATION SCHEME FOR SYSTEM OF VARIATIONAL INCLUSIONS USING GENERALIZED YOSIDA AND CAYLEY OPERATORS
-
Abstract
The aim of this work is to study a system of variational inclusions involving generalized Yosida and Cayley operators through inertial extrapolation scheme in real Banach space. To obtain faster convergence of the sequences generated by algorithm, we use one inertial extrapolation scheme, although we have established some more iterative schemes. To achieve our goal, we prove an important Lemma ensuring the convergence of sum of two sequences. We provide a numerical example.
-
Keywords:
- Cayley /
- Yosida /
- solution /
- convergence /
- scheme
-

-
References
[1] R. Ahmad, I. Ali, X. B. Li and M. Ishtyak, System of multi-valued mixed variational inclusions with XOR-operation in real ordered uniformly smooth Banach spaces, Mathematics, 2019, 7(1027). [2] R. Ahmad, I. Ali, M. Rahaman and M. Ishtyak, Cayley inclusion problem with its corresponding generalized resolvent equation problem in uniformly smooth Banach spaces, Appl. Anal., 2022, 101, 1354–1368. doi: 10.1080/00036811.2020.1781822 [3] R. Ahmad, M. Ishtyak, A. K. Rajpoot and Y. Wang, Solving system of mixed variational inclusions involving generalized Cayley operator and generalized Yosida approximation operator with error terms in $q$-uniformly smooth space, Mathematics, 2022, 10, 4131. doi: 10.3390/math10214131 CrossRef $q$-uniformly smooth space" target="_blank">Google Scholar
[4] I. Ahmad, J. C. Yao, R. Ahmad and M. Ishtyak, System of Yosida inclusions involving XOR-operation, J. Nonlinear Convex Anal., 2017, 18, 831–845. [5] B. Ali, A. A. Adam and A. Adamu, An accelerated algorithm involving quasi-$\phi$-nonexpansive operators for solving split problems, Journal of Nonlinear Modeling and Analysis, 2023, 5(1), 54–72. $\phi$-nonexpansive operators for solving split problems" target="_blank">Google Scholar
[6] S. Althubiti and A. Mennouni, A novel-projection method for Cayley-type systems of singular integro-differential equations, Mathematics, 2022, 10, 2694. doi: 10.3390/math10152694 [7] Q. H. Ansari and J. C. Yao, A fixed point theorem and its applications to system of variational inequalities, Bull. Austral. Math. Soc., 1999, 59, 433–442. doi: 10.1017/S0004972700033116 [8] C. L. Byrne, A unified treatment of some iterative algorithm in signal processing and image reconstruction, Inverse Problem, 2004, 20, 103–120. doi: 10.1088/0266-5611/20/1/006 [9] A. Cayley, Sur quelques propriétés des déterminants gauches, J. Reine Angew. Math., 1846, 1846(32), 119–123. doi: 10.1515/crll.1846.32.119 [10] L. C. Ceng, S. M. Guu and J. C. Yao, Hybrid viscosity CQ method for finding a common solution of a variational inequality, a general system of variational ineqaulities and a fixed point theorem, Fixed Point Theory Appl., 2013, 313, 1–25. [11] L. C. Ceng, A. Latif and J. C. Yao, On solutions of a system of variational inequalities and fixed point problems in Banach spaces, Fixed Point Theory Appl., 2013, 176, 1–34. [12] L. C. Ceng, S. Plubtring, M. M. Wong and J. C. Yao, System of variational inequalities with constraints of mixed equilibria, variational inequalities, convex minimization and fixed point problems, J. Nonlinear Convex Anal., 2015, 16, 385–421. [13] L. C. Ceng, C. Y. Wang and J. C. Yao, Strong convergence theorems by a relaxed extra gradient method for a general system of variational inequalities, Math. Methods Oper. Res., 2008, 67, 375–390. [14] A. De, Hille-Yosida Theorem and Some Applications, Ph. D. Thesis, Department of Mathematics and its Applications, Central European University, Budapest, Hungary, 2015. [15] X. Fang and M. Huang, The monotonicity of the linear complementarity problem, Journal of Nonlinear Modeling and Analysis, 2022, 4(2), 161–170. [16] Y. P. Fang and N. J. Huang, $H$-accretive operators and resolvent operator technique for solving variational inclusions in Banach spaces, Appl. Math. Lett., 2004, 17, 647–653. [17] J. Feng, W. Li, H. Chen and Y. Chen, A class of differential inverse variational inequalities in finite dimensional spaces, Journal of Applied Analysis and Computation, 2018, 8(6), 1664–1678. doi: 10.11948/2018.1664 [18] G. Helmberg, Introduction to Spectral Theory in Hilbert Space: The Cayley Transform, North-Holland Series in Applied Mathematics and Mechanics, Applied Mathematics and Mechanics # 6, North-Holland Publishing Company: Amesterdam, The Netherlands, 1969. [19] J. Iqbal, A. K. Rajpoot, M. Islam, R. Ahmad and Y. Wang, System of generalized variational inclusions involving Cayley operators and XOR-operation in $q$-uniformly smooth Banach spaces, Mathematics, 2022, 10, 2837. $q$-uniformly smooth Banach spaces" target="_blank">Google Scholar
[20] S. Jabeen, M. A. Noor and K. I. Noor, Inertial iterative methods for general quasi-variational inequalities and dynamical systems, J. Math. Anal., 2020, 11, 14–29. [21] C. Li and S. Wu, A two-step matrix splitting method for the mixed linear complementarity problem, Journal of Applied Analysis and Computation, 2024, 14(5), 2750–2761. [22] J. S. Pang, Asymmetric variational inequality problems over product of sets: Applications and iterative methods, Math. Program, 1985, 31, 206–219. [23] B. T. Polyak, Some methods of speeding up the convergence of iterative methods, USSR Comput. Math. Phys., 1964, 4, 1–17. [24] X. Qin, S. S. Chang, Y. J. Cho and S. M. Kang, Approximation of solutions to a system of variational inclusions in Banach spaces, J. Inequal. Appl., 2010, 2010, 916806. [25] B. Tan and S. Y. Cho, An inertial Mann-like algorithm for fixed points of non-expansive mappings in Hilbert spaces, J. Appl. Numer. Optim., 2020, 2, 335–351. [26] B. Tan and S. Li, Strong convergence of inertial Mann algorithm for solving hierarchical fixed point problems, J. Nonlinear Var. Anal., 2020, 4, 337–355. [27] W. Y. Yan, Y. P. Fang and N. J. Huang, A new system of set-valued variational inclusions with $H$-monotone operators, Math. Inequal. Appl., 2005, 8, 537–546. [28] C. Zhu, J. Chen, J. Chen, C. Chen and H. Huang, A new generalization of F-metric spaces and some fixed point theorems and an application, J. Appl. Anal. Comput., 2021, 11, 2649–2663. -
-
-
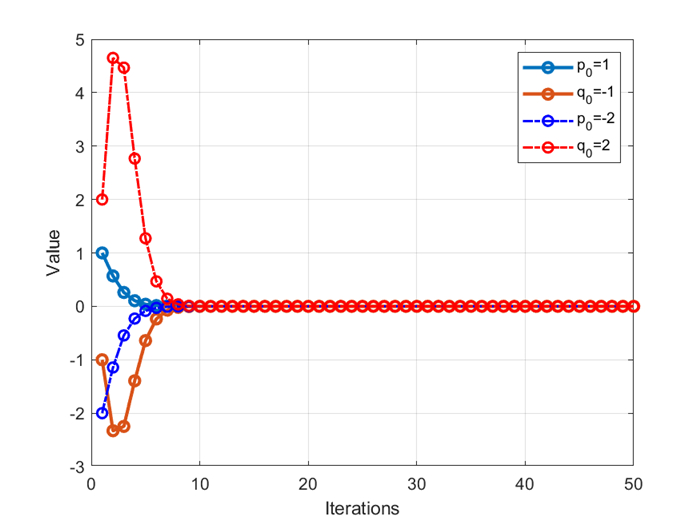
Figure 1.
Convergence Graph for different initial values of
$ \widehat{{\rm{p}}} $ $ \widehat{{\rm{q}}} $




 DownLoad:
DownLoad: