| Citation: | Shelly Arora, S. S. Dhaliwal, Wen Xiu Ma, Atul Pasrija. ANALYSIS OF FRACTIONAL ORDER SCHR$\ddot{O}$DINGER EQUATION WITH SINGULAR AND NON-SINGULAR KERNEL DERIVATIVES VIA NOVEL HYBRID SCHEME[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 1039-1067. doi: 10.11948/20240246 |
ANALYSIS OF FRACTIONAL ORDER SCHR$\ddot{O}$DINGER EQUATION WITH SINGULAR AND NON-SINGULAR KERNEL DERIVATIVES VIA NOVEL HYBRID SCHEME
-
Abstract
In the present study, a novel semi-analytic scheme is proposed to obtain exact and approximate series solutions for the time fractional linear and non-linear Schr$ \ddot{o} $dinger equation. This hybrid scheme employs the general bivariate transform followed by the homotopy perturbation method to formulate the recurrence relation. The recurrence relation leads to a system of linear differential equations that associates with the desired components of the series solution. To characterize the considered model with memory effects, the fractional temporal order is considered in the Caputo, Caputo-Fabrizio, and Atangana-Baleanu in Caputo senses. The adapted scheme appears efficient and competent in identifying a diverse collection of trigonometric, wave, and soliton solutions with the availability of initial data. Configurational variations in the governing phenomena with alterations in the fractional order are addressed through graphical illustrations. The potential of the developed regime is affirmed through the uniqueness and convergence analysis of the acquired results. Numerical results are found to be in accordance with existing results in terms of absolute error norms. The main highlight of the proposed scheme is its efficacy and simplicity in constructing a series solution that rapidly converges to the exact solution.
-

-
References
[1] S. Abbasbandy, Iterated He's homotopy perturbation method for quadratic Riccati differential equation, Applied Mathematics and Computation, 2006, 175(1), 581–589. doi: 10.1016/j.amc.2005.07.035 [2] R. K. Adivi Sri Venkata, A. Kirubanandam and R. Kondooru, Numerical solutions of time fractional Sawada Kotera Ito equation via natural transform decomposition method with singular and non-singular kernel derivatives, Mathematical Methods in the Applied Sciences, 2021, 44(18), 14025–14040. doi: 10.1002/mma.7672 [3] L. Akinyemi, K. S. Nisar, C. A. Saleel, H. Rezazadeh, P. Veeresha, M. M. Khater and M. Inc, Novel approach to the analysis of fifth-order weakly non-local fractional Schrödinger equation with Caputo derivative, Results in Physics, 2021, 31, 104958. doi: 10.1016/j.rinp.2021.104958 [4] G. Akram, M. Sadaf and I. Zainab, Effect of a new local derivative on space-time fractional non-linear Schrödinger equation and its stability analysis, Optical and Quantum Electronics, 2023, 55(9), 834. doi: 10.1007/s11082-023-05009-y [5] A. Ali, J. Ahmad and S. Javed, Exploring the dynamic nature of soliton solutions to the fractional coupled non-linear Schrödinger model with their sensitivity analysis, Optical and Quantum Electronics, 2023, 55(9), 810. doi: 10.1007/s11082-023-05033-y [6] A. Ali, A. R. Seadawy and D. Lu, Soliton solutions of the non-linear Schrödinger equation with the dual power law non-linearity and resonant non-linear Schrödinger equation and their modulation instability analysis, Optik, 2017, 145, 79–88. doi: 10.1016/j.ijleo.2017.07.016 [7] K. K. Ali and M. Maneea, Optical solitons using optimal homotopy analysis method for time-fractional (1+1)-dimensional coupled non-linear Schrödinger equations, Optik, 2023, 283, 170907. doi: 10.1016/j.ijleo.2023.170907 [8] K. K. Ali, M. Maneea and M. S. Mohamed, Solving nonlinear fractional models in superconductivity using the q-homotopy analysis transform method, Journal of Mathematics, 2023, 2023, 6647375. [9] S. A. Alsallami, M. Maneea, E. M. Khalil, S. Abdel-Khalek and K. K. Ali, Insights into time fractional dynamics in the Belousov-Zhabotinsky system through singular and non-singular kernels, Scientific Reports, 2023, 13(1), 22347. doi: 10.1038/s41598-023-49577-1 [10] I. G. Ameen, R. O. A. Taie and H. M. Ali, Two effective methods for solving non-linear coupled time-fractional Schrödinger equations, Alexandria Engineering Journal, 2023, 70, 331–347. doi: 10.1016/j.aej.2023.02.046 [11] V. D. Ao, D. V. Tran, K. T. Pham, D. M. Nguyen, H. D. Tran, T. K. Do, V. H. Do and T. V. Phan, A Schrödinger equation for evolutionary dynamics, Quantum Reports, 2023, 5(4), 659–682. doi: 10.3390/quantum5040042 [12] V. E. Arkhincheev, Anomalous diffusion in inhomogeneous media: Some exact results, Modelling Measurement and Control a General Physics Electronics and Electrical Engineering, 1993, 49, 11. [13] S. Arora and A. Pasrija, A novel integral transform operator and its applications, Iranian Journal of Numerical Analysis and Optimization, 2023, 13(3), 553–575. [14] S. Arshad, I. Saleem, A. Akgül, J. Huang, Y. Tang and S. M. Eldin, A novel numerical method for solving the Caputo-Fabrizio fractional differential equation, AIMS Math., 2023, 8(4), 9535–9556. doi: 10.3934/math.2023481 [15] A. Atangana and D. Baleanu, New fractional derivatives with non-local and non-singular kernel, Thermal Science, 2016, 20(2), 763–769. doi: 10.2298/TSCI160111018A [16] R. P. Bell, The application of quantum mechanics to chemical kinetics, Proceedings of the Royal Society of London, 1933, 139(838), 466–474. [17] M. Bilal, J. Ren, M. Inc and R. K. Alhefthi, Optical soliton and other solutions to the non-linear dynamical system via two efficient analytical mathematical schemes, Optical and Quantum Electronics, 2023, 55(11), 938. doi: 10.1007/s11082-023-05103-1 [18] M. Born, Quantenmechanik der stoßvorgänge, Zeitschrift für Physik, 1926, 38(11), 803–827. [19] M. Caputo and M. Fabrizio, A new definition of fractional derivative without singular kernel, Progress in Fractional Differentiation & Applications, 2015, 1(2), 73–85. [20] A. Chabchoub and R. H. Grimshaw, The hydrodynamic non-linear Schrödinger equation: Space and time, Fluids, 2016, 1(3), 23. doi: 10.3390/fluids1030023 [21] K. S. Cole, Electric Conductance of Biological Systems, Cold Spring Harbor Laboratory Press, NY, USA, 1933. [22] V. D. Djordjevic and T. M. Atanackovic, Similarity solutions to non-linear heat conduction and Burgers/Korteweg–deVries fractional equations, Journal of Computational and Applied Mathematics, 2008, 222(2), 701–714. doi: 10.1016/j.cam.2007.12.013 [23] S. O. Edeki, G. O. Akinlabi and S. A. Adeosun, Analytic and numerical solutions of time-fractional linear Schrödinger equation, Communications in Mathematics and Applications, 2016, 7(1), 1–10. [24] Z. Y. Fan, K. K. Ali, M. Maneea, M. Inc and S. W. Yao, Solution of time fractional Fitzhugh–Nagumo equation using semi analytical techniques, Results in Physics, 2023, 51, 106679. doi: 10.1016/j.rinp.2023.106679 [25] A. Ghorbani, Beyond Adomian polynomials: He polynomials, Chaos, Solitons & Fractals, 2009, 39(3), 1486–1492. [26] W. G. Glöckle and T. F. Nonnenmacher, A fractional calculus approach to self-similar protein dynamics, Biophysical Journal, 1995, 68(1), 46–53. doi: 10.1016/S0006-3495(95)80157-8 [27] S. H. Hamed, E. A. Yousif and A. I. Arbab, Analytic and approximate solutions of the space-time fractional Schrödinger equations by homotopy perturbation Sumudu transform method, in Abstract and Applied Analysis, 2014, 2014, 863015. [28] J. H. He, Homotopy perturbation method: A new non-linear analytical technique, Applied Mathematics and Computation, 2003, 135(1), 73–79. doi: 10.1016/S0096-3003(01)00312-5 [29] B. Hong, J. Wang and C. Li, Analytical solutions to a class of fractional coupled non-linear Schrödinger equations via Laplace-HPM technique, AIMS Math., 2023, 8(7), 15670–15688. doi: 10.3934/math.2023800 [30] Z. Z. Kang, T. C. Xia and W. X. Ma, Riemann–Hilbert approach and N-soliton solution for an eighth-order non-linear Schrödinger equation in an optical fiber, Advances in Difference Equations, 2019, 2019, 188. doi: 10.1186/s13662-019-2121-5 [31] M. Kapoor, Analytical approach for solution of linear and non-linear time-fractional Schrödinger equations by employing Sumudu transform iterative method, International Journal of Applied and Computational Mathematics, 2023, 9(3), 38. doi: 10.1007/s40819-023-01508-4 [32] A. Khan, A. Ali, S. Ahmad, S. Saifullah, K. Nonlaopon and A. Akgül, Non-linear Schrödinger equation under non-singular fractional operators: A computational study, Results in Physics, 2022, 43, 106062. doi: 10.1016/j.rinp.2022.106062 [33] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and Applications of Fractional Differential Equations, Elsevier, the Netherlands, 2006. [34] Y. S. Kivshar and G. P. Agrawal, Optical Solitons: From Fibers to Photonic Crystals, Academic Press, USA, 2003. [35] N. M. Kocherginsky, Interpretation of Schrödinger equation based on classical mechanics and spin, Quantum Studies: Mathematics and Foundations, 2021, 8(2), 217–227. doi: 10.1007/s40509-020-00240-8 [36] B. T. Krishna, Studies on fractional order differentiators and integrators: A survey, Signal Processing, 2011, 91(3), 386–426. doi: 10.1016/j.sigpro.2010.06.022 [37] N. Laskin, Fractional market dynamics, Physica A: Statistical Mechanics and its Applications, 2000, 287(3–4), 482–492. [38] N. Laskin, Fractional quantum mechanics and Lévy path integrals, Physics Letters A, 2000, 268(4–6), 298–305. [39] N. Laskin, Fractional quantum mechanics, Physical Review E, 2000, 62(3), 3135. doi: 10.1103/PhysRevE.62.3135 [40] N. Laskin, Fractional Schrödinger equation, Physical Review E, 2002, 66(5), 056108. doi: 10.1103/PhysRevE.66.056108 [41] M. Lechelon, Y. Meriguet, M. Gori, S. Ruffenach, I. Nardecchia, E. Floriani, D. Coquillat, S. Teppe, S. Mailfert, D. Marguet and P. Ferrier, Experimental evidence for long-distance electrodynamic intermolecular forces, Science Advances, 2022, 8(7), eabl5855. doi: 10.1126/sciadv.abl5855 [42] E. K. Lenzi, E. C. Gabrick, E. Sayari, A. S. de Castro, J. Trobia and A. M. Batista, Anomalous relaxation and three-level system: A fractional Schrödinger equation approach, Quantum Reports, 2023, 5(2), 442–458. doi: 10.3390/quantum5020029 [43] W. X. Ma and M. Chen, Direct search for exact solutions to the non-linear Schrödinger equation, Applied Mathematics and Computation, 2009, 215(8), 2835–2842. doi: 10.1016/j.amc.2009.09.024 [44] K. S. Miller and B. Ross, An Introduction to the Fractional Calculus and Fractional Differential Equations, John Wiley & Sons, New York, 1993. [45] I. Podlubny, Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and some of their Applications, Academic Press, USA, 1998. [46] A. Qazza, A. Burqan and R. Saadeh, A new attractive method in solving families of fractional differential equations by a new transform, Mathematics, 2021, 9(23), 3039. doi: 10.3390/math9233039 [47] S. Z. Rida, H. M. El-Sherbiny and A. A. M. Arafa, On the solution of the fractional non-linear Schrödinger equation, Physics Letters A, 2008, 372(5), 553–558. doi: 10.1016/j.physleta.2007.06.071 [48] R. Saadeh, A. Qazza and A. Burqan, A new integral transform: ARA transform and its properties and applications, Symmetry, 2020, 12(6), 925. doi: 10.3390/sym12060925 [49] R. Z. Saadeh and B. F. A. Ghazal, A new approach on transforms: Formable integral transform and its applications, Axioms, 2021, 10(4), 332. doi: 10.3390/axioms10040332 [50] L. J. Shen, Fractional derivative models for viscoelastic materials at finite deformations, International Journal of Solids and Structures, 2020, 190, 226–237. [51] H. Tariq, M. Sadaf, G. Akram, H. Rezazadeh, J. Baili, Y. P. Lv and H. Ahmad, Computational study for the conformable non-linear Schrödinger equation with cubic–quintic–septic non-linearities, Results in Physics, 2021, 30, 104839. [52] A. M. Wazwaz and G. Q. Xu, Bright, dark and Gaussons optical solutions for fourth-order Schrödinger equations with cubic–quintic and logarithmic non-linearities, Optik, 2020, 202, 163564. [53] Y. Xie, Z. Yang and L. Li, New exact solutions to the high dispersive cubic–quintic non-linear Schrödinger equation, Physics Letters A, 2018, 382(36), 2506–2514. [54] T. Xu, B. Tian, L. L. Li, X. Lü and C. Zhang, Dynamics of Alfvén solitons in inhomogeneous plasmas, Physics of Plasmas, 2008, 15(10), 102307. [55] N. Zettili, Quantum Mechanics: Concepts and Applications, 2nd Ed., John Wiley & Sons, Chichester, UK, 2009. [56] M. X. Zhou, A. R. Kanth, K. Aruna, K. Raghavendar, H. Rezazadeh, M. Inc and A. A. Aly, Numerical solutions of time fractional Zakharov-Kuznetsov equation via natural transform decomposition method with non-singular kernel derivatives, Journal of Function Spaces, 2021, 2021, 9884027. -
-
-
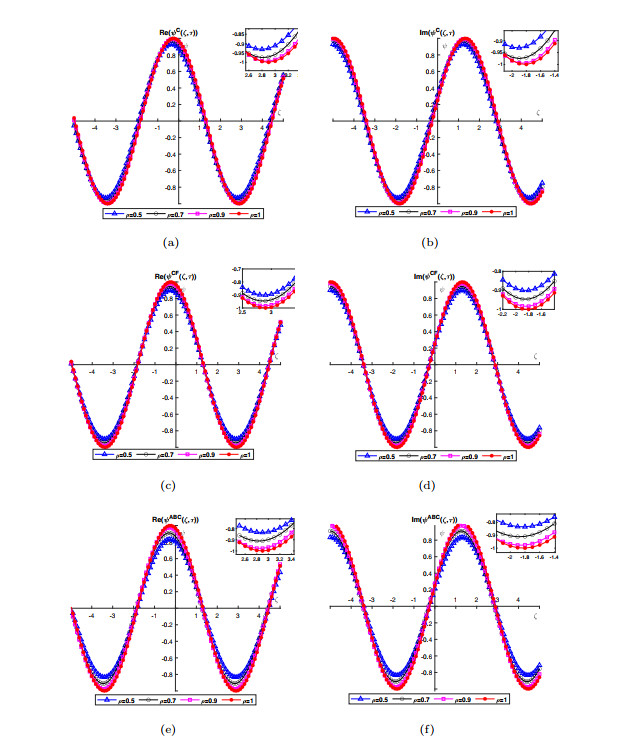
Figure 1.
Waveform behavior of real (Re) and imaginary (Im) part of GB-HPM solution for Caputo, CF and ABC operators at
$ \tau=0.5 $ -
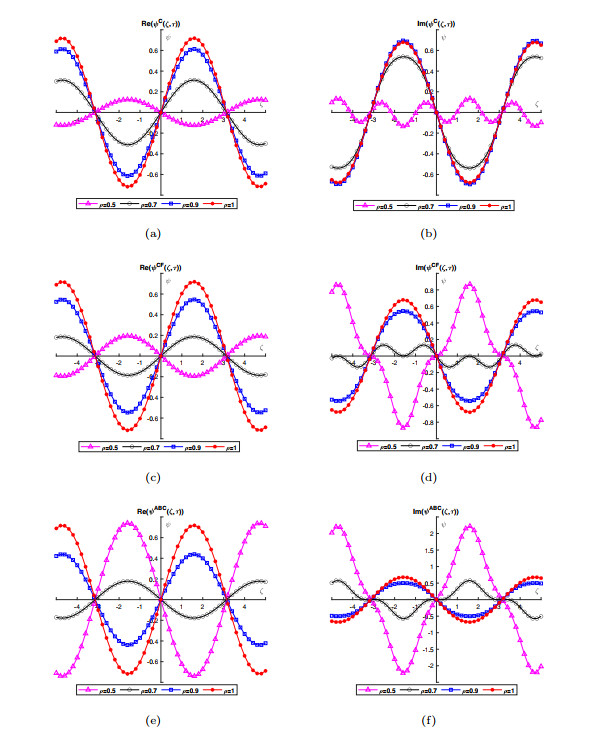
Figure 2.
Waveform behavior of real (Re) and imaginary (Im) part of GB-HPM solution for Caputo, CF and ABC operators at
$ \tau=0.5 $ -
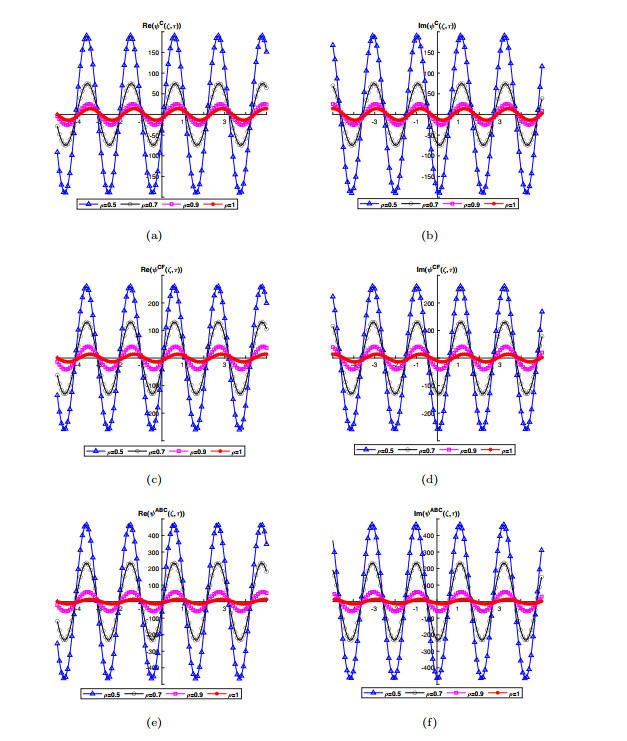
Figure 3.
Waveform behavior of real (Re) and imaginary (Im) part of GB-HPM solution for Caputo, CF and ABC operators at
$ \tau=0.5 $




 DownLoad:
DownLoad: