| Citation: | Vikash Kumar Sinha, Prashanth Maroju. AN EFFECTIVE NUMERICAL ALGORITHM FOR SOLVING THE LANE-EMDEN TYPE EQUATION BASED ON THE VARIATIONAL ITERATION METHOD COUPLED WITH THE HOMOTOPY ANALYSIS METHOD[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 1091-1106. doi: 10.11948/20240255 |
AN EFFECTIVE NUMERICAL ALGORITHM FOR SOLVING THE LANE-EMDEN TYPE EQUATION BASED ON THE VARIATIONAL ITERATION METHOD COUPLED WITH THE HOMOTOPY ANALYSIS METHOD
-
Abstract
This research introduces an effective numerical algorithm to determine the numerical solution of the Lane-Emden equation. This method is based on the variational iteration method coupled with the homotopy analysis method. We also included the convergence study of the proposed algorithm. Eight application problems of the Lane-Emden type equation of various kinds with several types of initial and boundary conditions are included to demonstrate the efficacy and accuracy of the proposed algorithm. The numerical outcomes are contrasted with those obtained by other methods [12,20,21] and the exact solution. Unlike other methods, the proposed algorithm does not require discretization or perturbation and can be applied easily and accurately. The proposed method can solve complex problems with less computational work and computation time.
-

-
References
[1] H. Ahmed, Numerical solutions for singular lane-emden equations using shifted chebyshev polynomials of the first kind, Contemporary Mathematics, 2023, 132–149. DOI: 10.37256/cm.4120232254. [2] W. Al-Hayani, L. Alzubaidy and A. Entesar, Solutions of singular ivp's of lane-emden type by homotopy analysis method with genetic algorithm, Applied Mathematics & Information Sciences, 2017, 11(2), 407–416. [3] A. K. Dizicheh, S. Salahshour, A. Ahmadian and D. Baleanu, A novel algorithm based on the legendre wavelets spectral technique for solving the lane–emden equations, Applied Numerical Mathematics, 2020, 153, 443–456. doi: 10.1016/j.apnum.2020.02.016 [4] J. -H. He, Variational iteration method for autonomous ordinary differential systems, Applied Mathematics and Computation, 2000, 114(2–3), 115–123. [5] S. Liao, On the homotopy analysis method for nonlinear problems, Applied Mathematics and Computation, 2004, 147(2), 499–513. doi: 10.1016/S0096-3003(02)00790-7 [6] S. -J. Liao, The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems, Ph. D. thesis, Shanghai Jiao Tong University China, 1992. [7] J. Malele, P. Dlamini and S. Simelane, Solving lane–emden equations with boundary conditions of various types using high-order compact finite differences, Applied Mathematics in Science and Engineering, 2023, 31(1), 2214303. doi: 10.1080/27690911.2023.2214303 [8] Y. Öztürk and M. Gülsu, An approximation algorithm for the solution of the lane–emden type equations arising in astrophysics and engineering using hermite polynomials, Computational and Applied Mathematics, 2014, 33, 131–145. doi: 10.1007/s40314-013-0051-5 [9] R. C. Rach, A new definition of the adomian polynomials, Kybernetes, 2008, 37(7), 910–955. doi: 10.1108/03684920810884342 [10] Z. Sabir, H. A. Wahab, M. Umar, et al., Novel design of morlet wavelet neural network for solving second order lane–emden equation, Mathematics and Computers in Simulation, 2020, 172, 1–14. doi: 10.1016/j.matcom.2020.01.005 [11] N. Saha and R. Singh, An efficient new numerical algorithm for solving emden–fowler pantograph differential equation using laguerre polynomials, Journal of Computational Science, 2023, 72, 102108. doi: 10.1016/j.jocs.2023.102108 [12] M. Singh and A. K. Verma, An effective computational technique for a class of lane–emden equations, Journal of Mathematical Chemistry, 2016, 54, 231–251. doi: 10.1007/s10910-015-0557-8 [13] R. Singh, Solving coupled lane-emden equations by green's function and decomposition technique, International Journal of Applied and Computational Mathematics, 2020, 6(3), 80. doi: 10.1007/s40819-020-00836-z [14] R. Singh, H. Garg and V. Guleria, Haar wavelet collocation method for lane–emden equations with dirichlet, neumann and neumann–robin boundary conditions, Journal of Computational and Applied Mathematics, 2019, 346, 150–161. doi: 10.1016/j.cam.2018.07.004 [15] V. K. Sinha and P. Maroju, New development of variational iteration method using quasilinearization method for solving nonlinear problems, Mathematics, 2023, 11(4), 935. doi: 10.3390/math11040935 [16] V. K. Sinha and P. Maroju, Numerical solution of coupled lane–emden–fowler type equation by embedded quasilinearization method with homotopy analysis method, Indian Journal of Pure and Applied Mathematics, 2023, 1–11. DOI: 10.1007/s13226-023-00475-2. [17] V. K. Sinha and P. Maroju, Numerical algorithm for solving real-life application problems of lane–emden type equation, Journal of Computational Science, 2024, 75, 102185. doi: 10.1016/j.jocs.2023.102185 [18] V. K. Sinha and P. Maroju, Quasilinearization variational iteration method for system of nonlinear odes, Physica Scripta, 2024, 99(5), 055213. doi: 10.1088/1402-4896/ad37ad [19] D. Tiwari, A. K. Verma and C. Cattani, Wavelet solution of a strongly nonlinear lane–emden equation, Journal of Mathematical Chemistry, 2022, 60(10), 2054–2080. doi: 10.1007/s10910-022-01401-3 [20] Umesh and M. Kumar, Approximate solution of singular ivps of lane–emden type and error estimation via advanced adomian decomposition method, Journal of Applied Mathematics and Computing, 2021, 66, 527–542. doi: 10.1007/s12190-020-01444-2 [21] Umesh and M. Kumar, Numerical solution of singular boundary value problems using advanced adomian decomposition method, Engineering with Computers, 2021, 37, 2853–2863. doi: 10.1007/s00366-020-00972-6 [22] R. A. Van Gorder and K. Vajravelu, Analytic and numerical solutions to the lane–emden equation, Physics Letters A, 2008, 372(39), 6060–6065. doi: 10.1016/j.physleta.2008.08.002 [23] A. -M. Wazwaz, A new algorithm for solving differential equations of lane–emden type, Applied mathematics and computation, 2001, 118(2–3), 287–310. [24] A. Yıldırım and T. Öziş, Solutions of singular ivps of lane–emden type by homotopy perturbation method, Physics Letters A, 2007, 369(1–2), 70–76. -
-
-
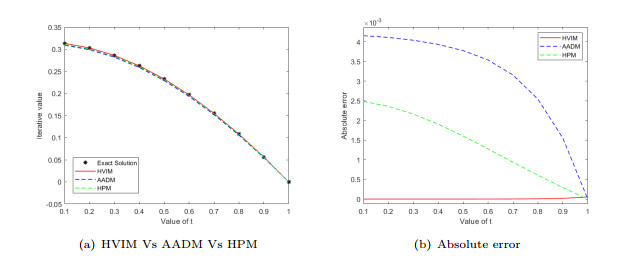
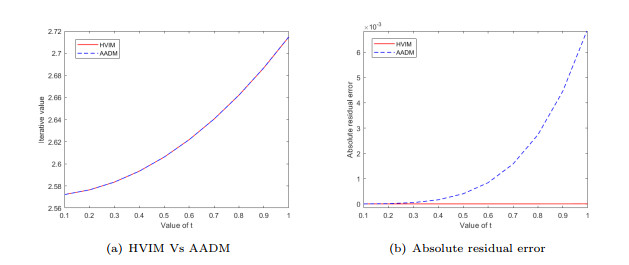
Figure 1.
Graphical comparison for Example 5.1.
-
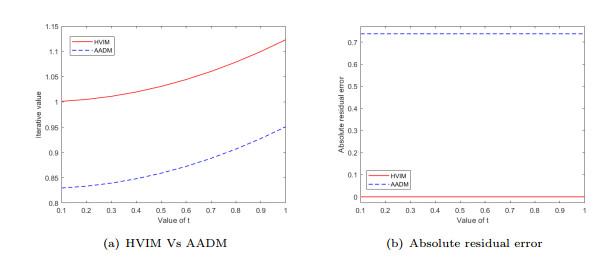
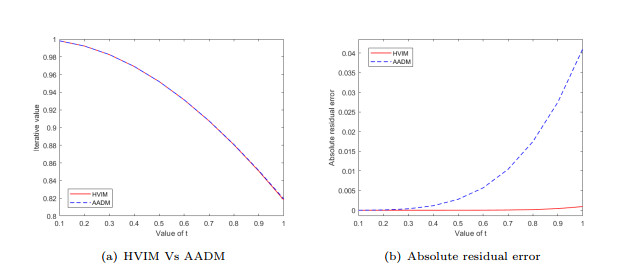
Figure 2.
Graphical comparison for Example 5.2.
-
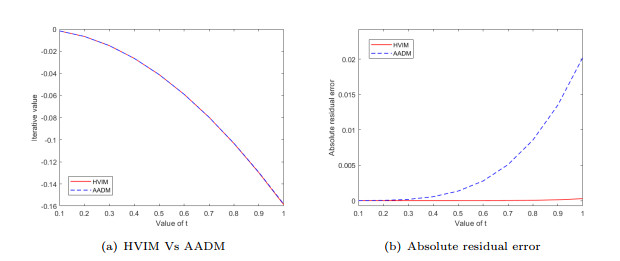
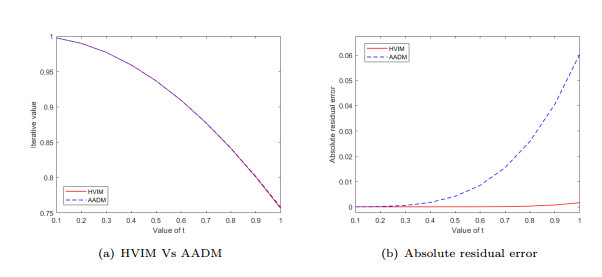
Figure 3.
Graphical comparison for Example 5.3.
-
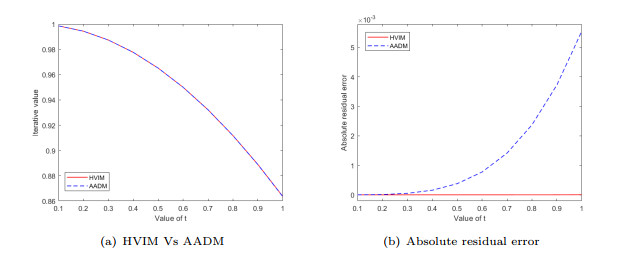
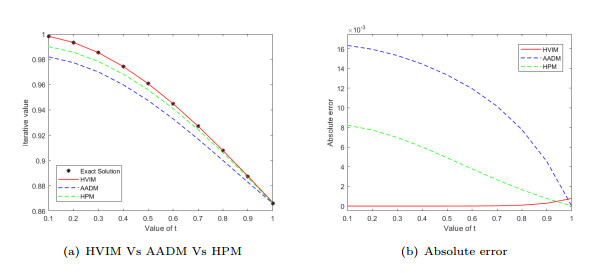
Figure 4.
Graphical comparison for Example 5.4.
-
Figure 5.
Graphical comparison for Example 5.5.
-
Figure 6.
Graphical comparison for Example 5.6.
-
Figure 7.
Graphical comparison for Example 5.7.
-
Figure 8.
Graphical comparison for Example 5.8.




 DownLoad:
DownLoad: