| Citation: | Lixin Liu. APPLICATIONS OF VARIATIONAL ITERATION METHOD TO A CLASS OF ORDINARY DIFFERENTIAL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 1107-1112. doi: 10.11948/20240276 |
APPLICATIONS OF VARIATIONAL ITERATION METHOD TO A CLASS OF ORDINARY DIFFERENTIAL EQUATIONS
-
Abstract
This paper proves the convergence of the variational iteration method for a class of $ n $-th order ordinary differential equations with Lipschitz nonlinearity which can be regarded as a generalization of oscillation equations.
-

-
References
[1] S. Cetinkaya and A. Demir, On applications Shehu variational iteration method to time fractional initial boundary value problems, Konuralp J. Math., 2024, 12(1), 13–20. [2] Y. Cui, S. Kang and H. Chen, Iterative positive solutions to nonlinear q-fractional differential equations with integral boundary value conditions, J. Nonl. Mod. Anal., 2023, 5, 446–455. [3] A. Entesar and O. Qasim, Solve fractional differential equations via a hybrid method between variational iteration method and gray wolf optimization algorithm, Asian-Eur. J. Math., 2021, 14(8), Paper No. 2150144, 9 pp. [4] J. He, Approximate analytical solution for seepage flow with fractional derivatives in porous media, Computer Methods in Applied Mechanics and Engineering, 1998, 1678, 57–68. [5] J. He, Approximate solution of nonlinear differential equations with convolution product nonlinearities, Computer Methods in Applied Mechanics and Engineering, 1998, 167, 69–73. doi: 10.1016/S0045-7825(98)00109-1 [6] J. He, Variational iteration method-a kind of non-linear analytical technique: Some examples, International Journal of Non-linear Mechanics, 1999, 34, 699–708. doi: 10.1016/S0020-7462(98)00048-1 [7] J. He, Variational approach for nonlinear oscillators, Chaos, Solitons & Fractals, 2007, 34, 1430–1439. [8] J. He, A short remark on fractional variational iteration method, Phys. Lett. A, 2011, 375(38), 3362–3364. doi: 10.1016/j.physleta.2011.07.033 [9] J. He and X. Wu, Construction of solitary solution and compacton-like solution by variational iteration method, Chaos, Solitons & Fractals, 2006, 29, 108–113. [10] M. Inokuti, H. Sekine and T. Mura, General use of the Lagrange multiplier in nonlinear mathematical physics, Variational Methods in the Mechanics of Solids, 1978, 33, 156–162. [11] D. Kumar, H. Jassim, J. Singh and M. Diykh, Fractional Elzaki variational iteration method for solving nonlinear biological population model, Lect. Notes Netw. Syst., 2024, 952, Springer, Cham, 368–376. [12] G. Monzón, Fractional variational iteration method for higher-order fractional differential equations, J. Fract. Calc. Appl., 2024, 15(1), Paper No. 4, 15 pp. [13] M. Nadeem and J. He, He-Laplace variational iteration method for solving the nonlinear equations arising in chemical kinetics and population dynamics, J. Math. Chem., 2021, 59(5), 1234–1245. doi: 10.1007/s10910-021-01236-4 [14] A. Prakash and M. Kumar, He's variational iteration method for the solution of nonlinear Newell-Whitehead-Segel equation, J. Appl. Anal. Comput., 2016, 6(3), 738–748. [15] M. Rafei, D. Ganji, H. Daniali and H. Pashaei, The variational iteration method for nonlinear oscillators with discontinuities, Journal of Sound and Vibration, 2007, 305, 614–620. [16] N. Sharma, G. Alhawael, P. Goswami and S. Joshi, Variational iteration method for n-dimensional time-fractional Navier-Stokes equation, Appl. Math. Sci. Eng., 2024, 32(1), Paper No. 2334387, 20 pp. [17] M. Shirazian, A new acceleration of variational iteration method for initial value problems, Math. Comput. Simulation, 2023, 214, 246–259. [18] J. Wen, C. Yue, Z. Liu and D. O'Regan, A fractional Landweber iteration method for simultaneous inversion in a time-fractional diffusion equation, J. Appl. Anal. Comput., 2023, 13(6), 3374–3402. -
-
-
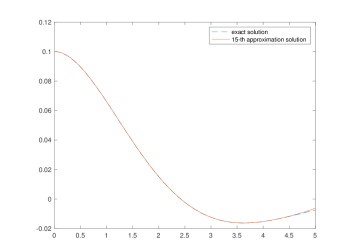
Figure 1.
-
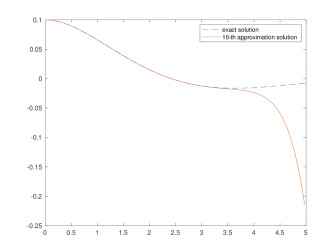
Figure 2.




 DownLoad:
DownLoad: