| Citation: | Mohammed M. A. Taleb, Saeed A. A. Al-Salehi, Shah Muhammad, V. C. Borkar. FIXED POINT THEOREMS OVER $\mathfrak{B}$-METRIC-LIKE SPACES AND APPLICATIONS IN ELECTRIC CIRCUIT EQUATIONS[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1430-1452. doi: 10.11948/20240259 |
FIXED POINT THEOREMS OVER $\mathfrak{B}$-METRIC-LIKE SPACES AND APPLICATIONS IN ELECTRIC CIRCUIT EQUATIONS
-
Abstract
In this article, we introduce the notion of $\alpha$-admissible crooked mapping with respect to $\theta$ with its special cases, which are $\alpha$-admissible crooked mapping with respect to $\theta^*$ and $\alpha^*$-admissible crooked mapping with respect to $\theta$. We present the notion of $(\beta\gamma, \alpha\theta, \psi F)$-rational contraction and establish new fixed point results over $\mathfrak{b}$-metric-like space. The study includes illustrative examples to support our results. Furthermore, we apply our results to prove the existence and uniqueness solution of the electric circuit equation, which is in second-order differential equation form.
-

-
References
[1] M. A. Alghamdi, N. Hussain and P. Salimi, Fixed point and coupled fixed point theorems on $b$-metric-like spaces, J. Inequal. Appl., 2013, 2013, 1–25. doi: 10.1186/1029-242X-2013-1 CrossRef $b$-metric-like spaces" target="_blank">Google Scholar
[2] M. Berzig, S. Chandok and M. S. Khan, Generalized Krasnoselskii fixed point theorem involving auxiliary functions in bimetric spaces and application to two-point boundary value problem, Appl. Math. Comput., 2014, 248, 323–327. [3] H. Bouhadjera, H. Z. Alzumi, W. Shammakh, S. M. Ali and M. S. Abdo, Unique common fixed points for occasionally weakly biased maps of type in-metric-like spaces, J. Funct. Spaces, 2023, 2023, 3937224. [4] S. S. Chauhan, K. Rana, M. Asim and M. Imdad, Geraghty type contractions in $b$-metric-like spaces, Korean J. Math., 2022, 30(4), 603–614. [5] C. Chen, L. Wen, J. Dong and Y. Gu, Fixed point theorems for generalized F-contractions in $b$-metric-like spaces, J. Nonlinear Sci. Appl., 2016, 9, 2161–2174. doi: 10.22436/jnsa.009.05.21 CrossRef $b$-metric-like spaces" target="_blank">Google Scholar
[6] S. Czerwik, Contraction mappings in $b$-metric spaces, Acta Math. Inform. Univ. Ostrav., 1993, 1(1), 5–11. [7] D. Gopal, M. Abbas and C. Vetro, Some new fixed point theorems in Menger PM-spaces with application to Volterra type integral equation, Appl. Math. Comput., 2014, 232, 955–967. [8] T. Hamaizia, Fixed point theorems for generalized $(\psi, \phi, F)$-contraction type mappings in $b$-metric spaces with applications, Open J. Math. Anal., 2021, 5, 35–41. doi: 10.30538/psrp-oma2021.0080 CrossRef $(\psi, \phi, F)$-contraction type mappings in
$b$ [9] H. A. Hammad and M. De la Sen, Fixed-point results for a generalized almost $(s, q)$-jaggi F-Contraction-Type on $b$-metric-like spaces, Mathematics, 2020, 8(1), 63. doi: 10.3390/math8010063 CrossRef $(s, q)$-jaggi F-Contraction-Type on
$b$ [10] H. Huang, G. Deng and S. Radenovic, Fixed point theorems for C-class functions in $b$-metric spaces and applications, Nonlinear Sci. Appl., 2017, 10, 5853–5868. doi: 10.22436/jnsa.010.11.23 CrossRef $b$-metric spaces and applications" target="_blank">Google Scholar
[11] H. Huang, K. Zoto, Z. D. Mitrovic and S. Radenovic, Fixed point results for generalized F-contractions in $b$-metric-like spaces, Fractal. Fract., 2022, 6(5), 272. doi: 10.3390/fractalfract6050272 CrossRef $b$-metric-like spaces" target="_blank">Google Scholar
[12] Z. Liu, X. Li, S. M. Kang and S. Y. Cho, Fixed point theorems for mappings satisfying contractive conditions of integral type and applications, Fixed Point Theory Appl., 2011, 2011, 1–18. doi: 10.1186/1687-1812-2011-1 [13] P. Saipara, K. Khammahawong and P. Kumam, Fixed‐point theorem for a generalized almost Hardy‐Rogers‐type F contraction on metric‐like spaces, Math. Meth. Appl. Sci., 2019, 42(17), 5898–5919. doi: 10.1002/mma.5793 [14] P. Salimi, A. Latif and N. Hussain, Modified $\alpha$-$\psi$-contractive mappings with applications, Fixed Point Theory Appl., 2013, 2013(1), 1–19. doi: 10.1186/1687-1812-2013-1 CrossRef $\alpha$-
$\psi$ [15] B. Samet, C. Vetro and P. Vetro, Fixed point theorems for $\alpha–\psi$-contractive type mappings, Nonlinear Anal., 2012, 75(4), 2154–2165. doi: 10.1016/j.na.2011.10.014 CrossRef $\alpha-\psi$-contractive type mappings" target="_blank">Google Scholar
[16] M. Taleb and V. C. Borkar, Some rational contraction and applications of fixed point theorems to F-metric space in differential equations, J. Math. Comput. Sci., 2022, 12, 133. [17] M. Taleb and V. C. Borkar, New fixed point results for some rational contraction on $(\phi, \psi)$-metric spaces, Sahand Commun. Math. Anal., 2024, 21(1), 47–66. $(\phi, \psi)$-metric spaces" target="_blank">Google Scholar
[18] M. Taleb, S. Al-Salehi and V. C. Borkar, New fixed point results over orthogonal F-metric spaces and application in second-order differential equations, J. Nonlinear Model. Anal., 2024, 6(3), 825–840. [19] A. Tomar and R. Sharma, Some coincidence and common fixed point theorems concerning F-contraction and applications, J. Int. Math. Virtual Inst., 2018, 8, 181–198. [20] K. Zoto, H. Aydi and H. Alsamir, Generalizations of some contractions in $b$-metric-like spaces and applications to boundary value problems, Adv. Differ. Equ., 2021, 2021(1), 1–18. $b$-metric-like spaces and applications to boundary value problems" target="_blank">Google Scholar
[21] K. Zoto, M. Gardasevic-Filipovic, I. Vardhami, Z. Mitrović and S. Radenovic, General new results on $(\phi, \mathcal{F})$-contractions in $b$-metric-like-spaces, Axioms, 2023, 12(7), 672. $(\phi, \mathcal{F})$-contractions in
$b$ [22] K. Zoto, S. Radenovic and A. H. Ansari, On some fixed point results for $(s, p, \alpha)$-contractive mappings in $b$-metric-like spaces and applications to integral equations, Open Math., 2018, 16(1), 235–249. [23] K. Zoto, B. E. Rhoades and S. Radenovic, Some generalizations for $(\alpha-\psi, \phi)$-contractions in $b$-metric-like spaces and an application, Fixed Point Theory Appl., 2017, 2017, 1–20. [24] K. Zoto, I. Vardhami, D. Bajovic, Z. Mitrovic and S. Radenovic, On some novel fixed point results for generalized F-contractions in $b$-metric-like spaces with application, Comput. Model. Eng. Sci., 2023, 135(1), 673–686. $b$-metric-like spaces with application" target="_blank">Google Scholar
-
-
-
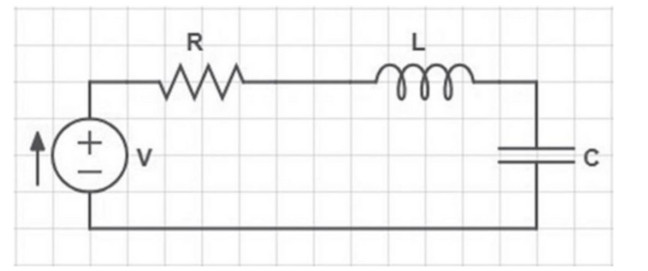
Figure 1.
Electric circuit.




 DownLoad:
DownLoad: