| Citation: |
Yiming Tang, Xin Wu, Rong Yuan, Fengjie Geng, Zhaohai Ma. ASYMPTOTIC BEHAVIOR OF A DELAYED NONLOCAL DISPERSAL LOTKA-VOLTERRA COMPETITIVE SYSTEM[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1453-1482. doi: 10.11948/20240262
|
ASYMPTOTIC BEHAVIOR OF A DELAYED NONLOCAL DISPERSAL LOTKA-VOLTERRA COMPETITIVE SYSTEM
-
Abstract
This paper investigates the asymptotic behavior of a nonlocal dispersal Lotka-Volterra competitive system with time delay across the entire $\mathbb{R}^N$. We establish $L^\infty-$decay estimates of solutions of linear systems converging to equilibria utilizing the Fourier transform method applied to the fundamental solution and the Fourier splitting technique. For the nonlinear time-delayed nonlocal dispersal Lotka-Volterra competitive system, we leverage the results from linear systems and obtain the long-time behavior of solutions of the nonlinear system manifesting as the form of time-exponential. More precisely, we further deduce $L^\infty-$decay estimates of solutions of the original nonlinear system through the properties of convolution and Hölder inequality. Additionally, numerical simulations are presented to bolster the principal theoretical results and illustrate that the time delay impedes species growth.
-
Keywords:
- Asymptotic stability /
- nonlocal dispersal /
- competitive system /
- Fourier transform
-
-
References
[1] A. Z. Akcasu and E. Daniels, Fluctuation analysis in simple fluids, Phys. Rev. A, 1970, 2(3), 962–975. doi: 10.1103/PhysRevA.2.962 [2] X. Bao, W.-T. Li, W. Shen, et al., Spreading speeds and linear determinacy of time dependent diffusive cooperative/competitive systems, J. Differential Equations, 2018, 265(7), 3048–3091. doi: 10.1016/j.jde.2018.05.003 [3] M. Bogoya, On non-local reaction-diffusion system in a bounded domain, Bound. Value Probl., 2018, 2018(1), 38. doi: 10.1186/s13661-018-0958-2 [4] E. Chasseigne, M. Chaves and J. D. Rossi, Asymptotic behavior for nonlocal diffusion equations, J. Math. Pures Appl., 2006, 86(3), 271–291. doi: 10.1016/j.matpur.2006.04.005 [5] R. Cherniha and V. Davydovych, Construction and application of exact solutions of the diffusive Lotka-Volterra system: A review and new results, Commun. Nonlinear Sci. Numer. Simul., 2022, 113, 106579. doi: 10.1016/j.cnsns.2022.106579 [6] C. Cortazar, M. Elgueta and J. D. Rossi, Nonlocal diffusion problems that approximate the heat equation with Dirichlet boundary conditions, Israel J. Math., 2009, 170(1), 53–60. doi: 10.1007/s11856-009-0019-8 [7] J. Coville and L. Dupaigne, Propagation speed of travelling fronts in nonlocal reaction-diffusion equations, Nonlinear Anal., 2005, 60(5), 797–819. doi: 10.1016/j.na.2003.10.030 [8] Y. Du and W. Ni, Spreading speed for some cooperative systems with nonlocal diffusion and free boundaries, part 1: Semi-wave and a threshold condition, J. Differential Equations, 2022, 308(25), 369–420. [9] G. Faye, Multidimensional stability of planar traveling waves for the scalar nonlocal Allen-Cahn equation, Discrete Contin. Dyn. Syst., 2016, 36(5), 2473–2496. [10] B.-S. Han and D.-Y. Kong, Propagation dynamics of a nonlocal reaction-diffusion system, Discrete Contin. Dyn. Syst., 2023, 43(7), 2756–2780. doi: 10.3934/dcds.2023028 [11] B.-S. Han, Y. Yang, W.-J. Bo, et al., Global dynamics of a Lotka-Volterra competition diffusion system with nonlocal effects, Int. J. Bifurcation Chaos, 2020, 30(05), 2050066. doi: 10.1142/S0218127420500662 [12] S.-B. Hsu, L. Mei and F.-B. Wang, On a nonlocal reaction-diffusion-advection system modelling the growth of phytoplankton with cell quota structure, J. Differential Equations, 2015, 259(10), 5353–5378. doi: 10.1016/j.jde.2015.06.030 [13] R. Huang, M. Mei and Y. Wang, Planar traveling waves for nonlocal dispersion equation with monostable nonlinearity, Discrete Contin. Dyn. Syst., 2012, 32(10), 3621–3649. doi: 10.3934/dcds.2012.32.3621 [14] R. Huang, M. Mei and Z. Wang, Threshold convergence results for a nonlocal time-delayed diffusion equation, J. Differential Equations, 2023, 364(15), 76–106. [15] R. Huang, M. Mei, K. Zhang, et al., Asymptotic stability of non-monotone traveling waves for time-delayed nonlocal dispersion equations, Discrete Contin. Dyn. Syst., 2016, 36(3), 1331–1353. [16] L. I. Ignat and J. D. Rossi, A nonlocal convection-diffusion equation, J. Funct. Anal., 2007, 251(2), 399–437. doi: 10.1016/j.jfa.2007.07.013 [17] L. I. Ignat and J. D. Rossi, Decay estimates for nonlocal problems via energy methods, J. Math. Pures Appl., 2009, 92(2), 163–187. doi: 10.1016/j.matpur.2009.04.009 [18] Z. Jia, Global boundedness of weak solutions for an attraction-repulsion chemotaxis system with p-Laplacian diffusion and nonlinear production, Discrete Contin. Dyn. Syst. Ser. B, 2023, 28(9), 4847–4863. doi: 10.3934/dcdsb.2023044 [19] B. Karami and D. Shahsavari, Nonlocal strain gradient model for thermal stability of FG nanoplates integrated with piezoelectric layers, Smart. Struct. Syst., 2019, 23(3), 215–225. [20] D. Y. Khusainov, A. F. Ivanov and I. V. Kovarzh, Solution of one heat equation with delay, Nonlinear Oscil., 2009, 12(2), 260–282. doi: 10.1007/s11072-009-0075-3 [21] A. Kolmogorov, I. Petrovskii and N. Piskunov, Study of a diffusion equation that is related to the growth of a quality of matter and its application to a biological problem, Mosc. Univ. Math. Bull., 1937, 1, 1–25. [22] C. T. Lee, M. F. Hoopes, J. Diehl, et al., Non-local concepts and models in biology, J. Theoret. Biol., 2001, 210(2), 201–219. doi: 10.1006/jtbi.2000.2287 [23] C. Lei, H. Li and Y. Zhao, Dynamical behavior of a reaction-diffusion SEIR epidemic model with mass action infection mechanism in a heterogeneous environment, Discrete Contin. Dyn. Syst. Ser. B, 2024, 29(7), 3163–3198. doi: 10.3934/dcdsb.2023216 [24] W.-T. Li, Y.-J. Sun and Z.-C. Wang, Entire solutions in the Fisher-KPP equation with nonlocal dispersal, Nonlinear Anal. Real World Appl., 2010, 11(4), 2302–2313. doi: 10.1016/j.nonrwa.2009.07.005 [25] W.-T. Li, J.-B. Wang and X.-Q. Zhao, Spatial dynamics of a nonlocal dispersal population model in a shifting environment, J. Nonlinear Sci., 2018, 28(4), 1189–1219. doi: 10.1007/s00332-018-9445-2 [26] G. Lin and W.-T. Li, Bistable wavefronts in a diffusive and competitive Lotka-Volterra type system with nonlocal delays, J. Differential Equations, 2008, 244(3), 487–513. doi: 10.1016/j.jde.2007.10.019 [27] Z. Ma, X. Wu and R. Yuan, Nonlinear stability of traveling wavefronts for competitive-cooperative Lotka-Volterra systems of three species, Appl. Math. Comput., 2017, 315(15), 331–346. [28] Z. Ma, X. Wu, R. Yuan, et al., Multidimensional stability of planar waves for delayed reaction-diffusion equation with nonlocal diffusion, J. Appl. Anal. Comput., 2019, 9(3), 962–980. [29] Z. Ma, R. Yuan, Y. Wang, et al., Multidimensional stability of planar traveling waves for the delayed nonlocal dispersal competitive Lotka-Volterra system, Commun. Pure Appl. Anal., 2019, 18(4), 2069–2092. doi: 10.3934/cpaa.2019093 [30] L. Mei and X. Zhang, On a nonlocal reaction-diffusion-advection system modeling phytoplankton growth with light and nutrients, Discrete Contin. Dyn. Syst. Ser. B, 2012, 17(1), 221–243. [31] M. Mei, C. Ou and X.-Q. Zhao, Global stability of monostable traveling waves for nonlocal time-delayed reaction-diffusion equations, SIAM J. Math. Anal., 2010, 42(6), 2762–2790. doi: 10.1137/090776342 [32] M. Mei, J. W.-H. So, M. Y. Li, et al., Asymptotic stability of travelling waves for Nicholson's blowflies equation with diffusion, Proc. Roy. Soc. Edinburgh Sect. A, 2004, 134(3), 579–594. doi: 10.1017/S0308210500003358 [33] J. D. Murray, Mathematical Biology, Springer-Verlag, Berlin, 1989. [34] S. Pan, W.-T. Li and G. Lin, Existence and stability of traveling wavefronts in a nonlocal diffusion equation with delay, Nonlinear Anal., 2010, 72(6), 3150–3158. doi: 10.1016/j.na.2009.12.008 [35] S. Ruan and X.-Q. Zhao, Persistence and extinction in two species reaction-diffusion systems with delays, J. Differential Equations, 1999, 156(1), 71–92. doi: 10.1006/jdeq.1998.3599 [36] M. E. Schonbek, Uniform decay rates for parabolic conservation laws, Nonlinear Anal., 1986, 10(9), 943–956. doi: 10.1016/0362-546X(86)90080-5 [37] Y. Sun and H. Yu, A unified non-local fluid transport model for heterogeneous saturated porous media, Comput. Meth. Appl. Mech. Eng., 2022, 389(1), 114294. [38] Y. Tang and F. Li, Multiple stable states for a class of predator-prey systems with two harvesting rates, J. Appl. Anal. Comput., 2024, 14(1), 506–514. [39] F. Andreu-Vaillo, J. M. Mazón, J. D. Rossi, et al., Nonlocal Diffusion Problems, American Mathematical Society, Providence, RI, 2010. [40] J. Wang, Z. Yu and Y. Meng, Existence and stability of invasion traveling waves for a competition system with random vs. nonlocal dispersals, Int. J. Biomath., 2019, 12(1), 1950004. doi: 10.1142/S1793524519500049 [41] M. Wang and G. Lv, Entire solutions of a diffusive and competitive Lotka-Volterra type system with nonlocal delays, Nonlinearity, 2010, 23(7), 1609–1630. doi: 10.1088/0951-7715/23/7/005 [42] M.-L. Wang, G.-B. Zhang and P. He, Invasion traveling waves of a three species Lotka-Volterra competitive system with nonlocal dispersal, Commun. Nonlinear Sci. Numer. Simul., 2024, 132, 107939. doi: 10.1016/j.cnsns.2024.107939 [43] X. Wang, Z. Wang and Z. Jia, Global weak solutions for an attraction-repulsion chemotaxis system with p-Laplacian diffusion and logistic source, Acta Math. Sci., 2024, 44(3), 909–924. doi: 10.1007/s10473-024-0308-7 [44] M. Xu, Nonlocal heat conduction in silicon nanowires and carbon nanotubes, Heat Mass Transf., 2020, 57(5), 843–852. [45] M. Xu, S. Liu and Y. Lou, Persistence and extinction in the anti-symmetric Lotka-Volterra systems, J. Differential Equations, 2024, 387(5), 299–323. [46] W.-B. Xu, W.-T. Li and G. Lin, Nonlocal dispersal cooperative systems: Acceleration propagation among species, J. Differential Equations, 2020, 268(3), 1081–1105. doi: 10.1016/j.jde.2019.08.039 [47] Z.-J. Yang and G.-B. Zhang, Speed selection for a Lotka-Volterra competitive system with local vs. nonlocal diffusions, Qual. Theory Dyn. Syst., 2023, 22(2), 43–59. doi: 10.1007/s12346-023-00747-6 [48] Z.-X. Yu and R. Yuan, Travelling wave solutions in nonlocal reaction-diffusion systems with delays and applications, ANZIAM J., 2009, 51(1), 49–66. doi: 10.1017/S1446181109000406 [49] A. M. Zenkour, A. E. Abouelregal, K. A. Alnefaie, et al., Nonlocal thermoelasticity theory for thermal-shock nanobeams with temperature-dependent thermal conductivity, J. Therm. Stresses, 2015, 38(9), 1049–1067. doi: 10.1080/01495739.2015.1038490 [50] G.-B. Zhang and R. Ma, Spreading speeds and traveling waves for a nonlocal dispersal equation with convolution-type crossing-monostable nonlinearity, Z. Angew. Math. Phys., 2013, 65(5), 819–844. [51] X. Zhang and R. Yuan, Stochastic bifurcation and density function analysis of a stochastic logistic equation with distributed delay and strong kernel, Int. J. Biomath., 2022, 16(03), 2250085. [52] X. Zhao and R. Yang, Dynamical property analysis of a delayed diffusive predator-prey model with fear effect, J. Nonl. Mod. Anal., 2023, 5(1), 1–23. [53] C. Zhu and Y. Peng, Stability and bifurcation analysis in a nonlocal diffusive predator-prey model with hunting cooperation, J. Nonl. Mod. Anal., 2023, 5(1), 95–107. -
-
Figures(8)
Export File
Citation
Yiming Tang, Xin Wu, Rong Yuan, Fengjie Geng, Zhaohai Ma. ASYMPTOTIC BEHAVIOR OF A DELAYED NONLOCAL DISPERSAL LOTKA-VOLTERRA COMPETITIVE SYSTEM[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1453-1482. doi: 10.11948/20240262
Format
Content
DownLoad:
-
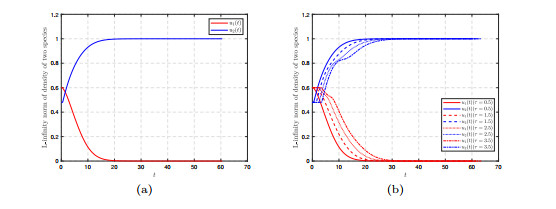
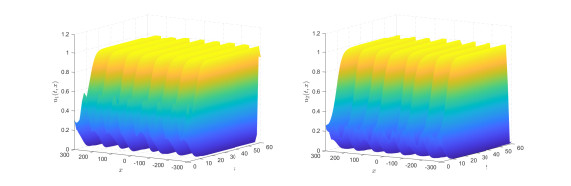
Figure 1.
The asymptotic behavior of the solution convergence to
$ E_1^{\ast} $ -
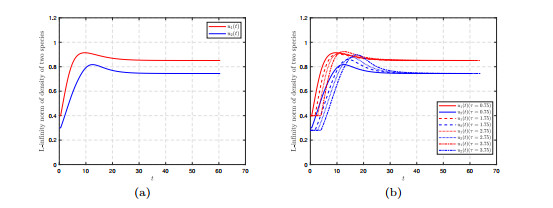
Figure 2.
(a)
$ L^\infty- $ $ \tau=0.5 $ $ 1.5 $ $ 2.5 $ $ 3.5 $ -
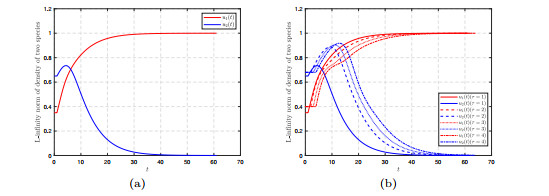
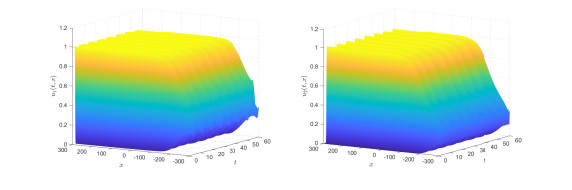
Figure 3.
The asymptotic behavior of the solution convergence to
$ E_2^{\ast} $ -
Figure 4.
(a)
$ L^\infty- $ $ \tau=1 $ $ 2 $ $ 3 $ $ 4 $ -
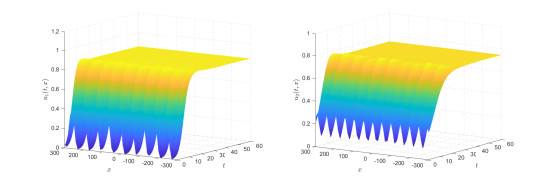
Figure 5.
The asymptotic behavior of the solution convergence to
$ E_3^{\ast} $ -
Figure 6.
(a)
$ L^\infty- $ $ \tau=0.75 $ $ 1.75 $ $ 2.75 $ $ 3.75 $ -
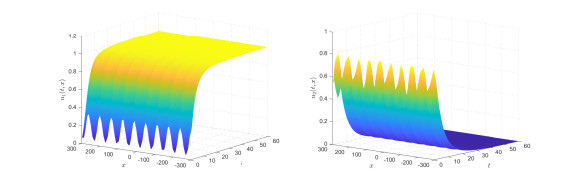
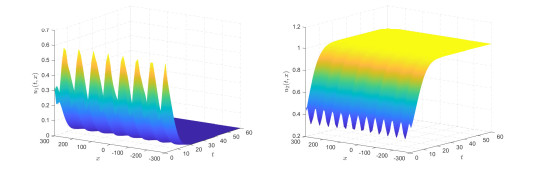
Figure 7.
The space periodic solution.
-
Figure 8.
The time periodic solution.