| Citation: | Aytura Keram, Pengzhan Huang. CONVERGENCE ANALYSIS OF THE UZAWA ITERATIVE METHOD FOR THE THERMALLY COUPLED STATIONARY INCOMPRESSIBLE MAGNETOHYDRODYNAMICS FLOW[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1563-1579. doi: 10.11948/20240292 |
CONVERGENCE ANALYSIS OF THE UZAWA ITERATIVE METHOD FOR THE THERMALLY COUPLED STATIONARY INCOMPRESSIBLE MAGNETOHYDRODYNAMICS FLOW
-
Abstract
In this paper, we designed an Uzawa iterative method for solving the thermally coupled stationary incompressible magnetohydrodynamics system, where a decoupled discrete system is obtained and no saddle point problem is required to deal with at each iterative step except the initial guess. Then, the convergence analysis of the presented method is provided. Finally, the effectiveness of the proposed method is illustrated with some numerical examples.
-

-
References
[1] D. N. Arnold, F. Brezzi and M. Fortin, A stable finite element for the Stokes equations, Calcolo, 1984, 21, 337–344. doi: 10.1007/BF02576171 [2] K. Arrow, L. Hurwicz and H. Uzawa, Studies in Nonlinear Programming, Standford University Press, Standford, 1958. [3] S. Badia, A. F. Martína and R. Planas, Block recursive LU preconditioners for the thermally coupled incompressible inductionless MHD problem, J. Comput. Phys., 2014, 274, 562–591. doi: 10.1016/j.jcp.2014.06.028 [4] A. Bermúdez, R. Muñoz-Sola and R. Vázquez, Analysis of two stationary magnetohydrodynamics systems of equations including Joule heating, J. Math. Anal. Appl., 2010, 368, 444–468. doi: 10.1016/j.jmaa.2010.03.046 [5] J. Boland and W. Layton, Error analysis for finite element methods for steady natural convection problems, Numer. Funct. Anal. Optimiz., 1990, 11, 449–483. doi: 10.1080/01630569008816383 [6] P. Chen, J. Huang and H. Sheng, Some Uzawa methods for steady incompressible Navier-Stokes equations discretized by mixed element methods, J. Comput. Appl. Math., 2015, 273, 313–325. doi: 10.1016/j.cam.2014.06.019 [7] A. Çıbık and W. Layton, Convergence of a Ramshaw-Mesina iteration, Appl. Math. Lett., 2024, 154, 109107. doi: 10.1016/j.aml.2024.109107 [8] R. Codina and N. Hernández, Approximation of the thermally coupled MHD problem using a stabilized finite element method, J. Comput. Phys., 2011, 230, 1281–1303. doi: 10.1016/j.jcp.2010.11.003 [9] Q. Q. Ding, X. N. Long and S. P. Mao, Convergence analysis of Crank-Nicolson extrapolated fully discrete scheme for thermally coupled incompressible magnetohydrodynamic system, Appl. Numer. Math., 2020, 157, 522–543. doi: 10.1016/j.apnum.2020.06.018 [10] X. J. Dong, Y. N. He and Y. Zhang, Convergence analysis of three finite element iterative methods for the 2D/3D stationary incompressible magnetohydrodynamics, Comput. Methods Appl. Mech. Engrg., 2014, 276, 287–311. doi: 10.1016/j.cma.2014.03.022 [11] J. F. Gerbeau, C. Le Bris and T. Lelièvre, Mathematical Methods for the Magnetohydrodynamics of Liquid Metals, Numerical Mathematics and Scientific Computation, Oxford University Press, Oxford, 2006. [12] V. Girault and P. A. Raviart, Finite Element Method for Navier-Stokes Equations: Theory and Algorithms, Springer-Verlag, New York, 1986. [13] M. D. Gunzburger, A. J. Meir and J. S. Peterson, On the existence, uniqueness, and finite element approximation of solutions of the equations of stationary, incompressible magnetohydrodynamics, Math. Comp., 1991, 56, 523–563. doi: 10.1090/S0025-5718-1991-1066834-0 [14] Y. N. He, Unconditional convergence of the Euler semi-implicit scheme for the 3D incompressible MHD equations, IMA J. Numer. Anal., 2015, 35, 767–801. doi: 10.1093/imanum/dru015 [15] Q. G. Hong, J. Kraus, M. Lymbery and F. Philo, Parameter-robust Uzawa-type iterative methods for double saddle point problems arising in Biot's consolidation and multiple-network poroelasticity models, Math. Mod. Meth. Appl. Sci., 2020, 30, 2523–2555. doi: 10.1142/S0218202520500499 [16] A. Keram and P. Z. Huang, An iterative method for the thermally coupled incompressible magnetohydrodynamics equations at high parameter, Mathematical Methods in the Applied Sciences, 2024. DOI: 10.1002/mma.9420. [17] S. J. Liu and P. Z. Huang, A grad-div stabilized method using the Jacobi iteration for the thermally coupled incompressible magnetohydrodynamic system, Z. Angew. Math. Mech., 2023, 103, e202200362. doi: 10.1002/zamm.202200362 [18] H. Ma and P. Huang, A fully discrete decoupled finite element method for the thermally coupled incompressible magnetohydrodynamic problem, J. Sci. Comput., 2023, 95, 14. doi: 10.1007/s10915-023-02131-7 [19] A. J. Meir, Thermally coupled magnetohydynamics flow, Appl. Math. Comput., 1994, 65, 79–94. [20] A. J. Meir, Thermally coupled, stationary, incompressible MHD flow; Existence uniqueness, and finite element approximation, Numer. Meth. Part. Differ. Equs., 1995, 11, 311–337. doi: 10.1002/num.1690110403 [21] A. J. Meir and P. G. Schmidt, On electronmagnetically and thermally driven liquid-metal flows, Nonliear Anal., 2001, 47, 3281–3294. doi: 10.1016/S0362-546X(01)00445-X [22] R. H. Nochetto and J. H. Pyo, Optimal relaxation parameter for the Uzawa method, Numer. Math., 2004, 98, 695–702. doi: 10.1007/s00211-004-0522-0 [23] H. Ouertani and M. Abdelwahed, The algorithmic resolution of spectral-element discretization for the time-dependent Stokes problem, Bound. Value. Probl., 2024, 89. [24] H. L. Qiu, Error analysis of Euler semi-implicit scheme for the nonstationary magnetohydrodynamics problem with temperature dependent parameters, J. Sci. Comput., 2020, 85, 1–26. doi: 10.1007/s10915-020-01306-w [25] S. S. Ravindran, A decoupled Crank-Nicolson time-stepping scheme for thermaly coupled magneto-hydrodynamic system, Inter. J. Optimiz. Control Theories Appl., 2018, 8, 2146–5703. [26] S. S. Ravindran, Partitioned time-stepping scheme for an MHD system with temperature-dependent coefficients, IMA J. Numer. Anal., 2019, 39, 1860–1887. doi: 10.1093/imanum/dry037 [27] M. Sheikholeslami, Influence of magnetic field on nanofluid free convection in an open porous cavity by means of lattice Boltzmann method, J. Mol. Liq., 2017, 234, 364–374. doi: 10.1016/j.molliq.2017.03.104 [28] J. T. Yang and T. Zhang, Stability and convergence of iterative finite element methods for the thermally coupled incompressible MHD flow, Int. J. Numer. Methods Heat fluid flow., 2020, 30, 5103–5141. doi: 10.1108/HFF-11-2019-0821 [29] X. W. Yang, P. Z. Huang and Y. N. He, A Voigt regularization of the thermally coupled magnetohydrodynamic flow, Z. Angew. Math. Phys., 2024, 75, 115. doi: 10.1007/s00033-024-02248-1 [30] H. F. Zhang and T. Zhang, Optimal error estimates of two-level iterative finite element methods for the thermally coupled incompressible MHD with different viscosities, Mathematical Methods in the Applied Sciences, 2024. DOI: 10.1002/mma.8800. [31] T. L. Zhu, H. Y. Su and X. L. Feng, Some Uzawa-type finite element iterative methods for the steady incompressible magnetohydrodynamic equations, Appl. Math. Comput., 2017, 302, 34–47. -
-
-
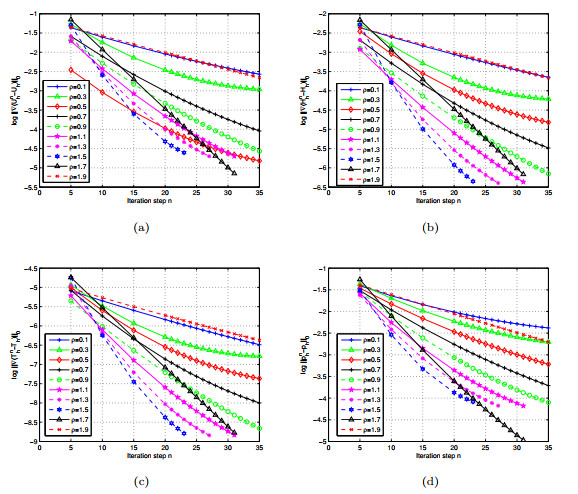
Figure 1.
The log errors of the velocity (a), magnetic (b), temperature (c) and pressure (d) at the different iterative steps.
-
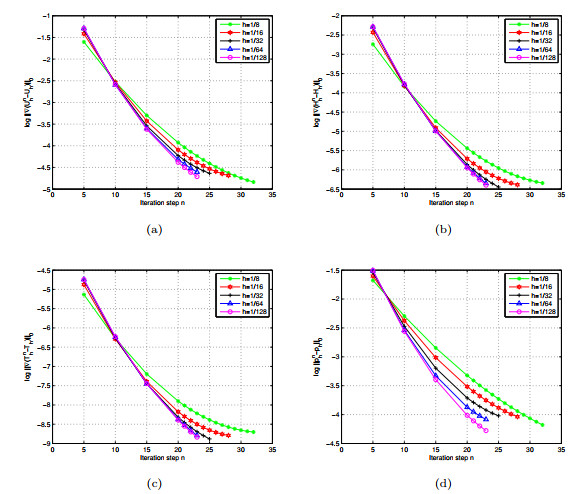
Figure 2.
The log errors of the velocity (a), magnetic (b), temperature (c) and pressure (d) at the different iterative steps.
-
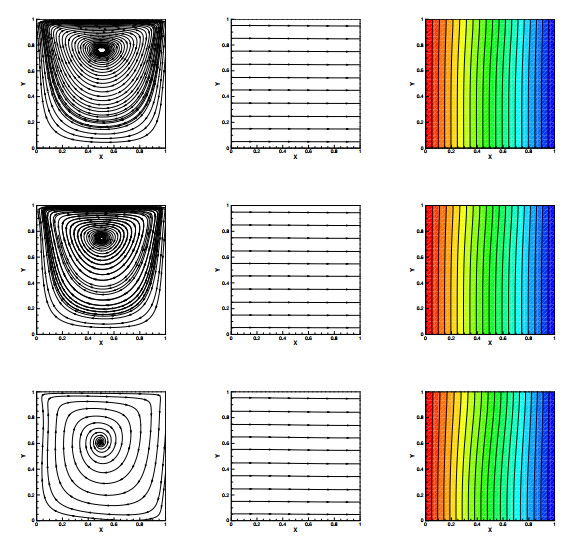
Figure 3.
Numerical velocity streamlines, magnetic and isotherms with different thermal expansion coefficient
$ \beta=1 $ $ \beta=10 $ $ \beta=100 $




 DownLoad:
DownLoad: