| Citation: | Krishna Murari Malav, Kapil Kant, Joydip Dhar, Gnaneshwar Nelakanti. DISCRETE MULTI-GALERKIN METHODS FOR DERIVATIVE-DEPENDENT HAMMERSTEIN TYPE WEAKLY SINGULAR NONLINEAR FREDHOLM INTEGRAL EQUATIONS WITH GREEN'S KERNEL[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1616-1640. doi: 10.11948/20240324 |
DISCRETE MULTI-GALERKIN METHODS FOR DERIVATIVE-DEPENDENT HAMMERSTEIN TYPE WEAKLY SINGULAR NONLINEAR FREDHOLM INTEGRAL EQUATIONS WITH GREEN'S KERNEL
-
Abstract
In this article, we study discrete multi-Galerkin and iterated discrete multi-Galerkin methods for solving the derivative-dependent nonlinear Hammerstein type Fredholm integral equations, where the nonlinear function within the integration is dependent on the derivative, and the kernel function is of Green's type. We achieve the error bounds by substituting all integrals in the multi-Galerkin method with numerical quadrature and obtain the superconvergence results for derivative-dependent Fredholm-Hammerstein integral equations using piecewise polynomials as basis functions. By applying the numerical quadrature rule, we prove that the iterated discrete multi-Galerkin method provides superior convergence rates over the discrete multi-Galerkin method with $\mathbb{O}(h^{\min(d+1,~m+2{m_{1}},~m+2{m_{2}})})$, where $h$ represents the norm of the partitions. Numerical results are presented to validate the theoretical findings, with figures illustrating a comparison of the error analysis between the proposed methods and those discussed in [22].
-

-
References
[1] J. A. Adam and S. A. Maggelakis, Mathematical models of tumor growth. Ⅳ. Effects of a necrotic core, Math. Biosci., 1989, 97(1), 121–136. doi: 10.1016/0025-5564(89)90045-X [2] G. Adomian, Solution of the Thomas-Fermi equation, Appl. Math. Lett., 1998, 11(3), 131–133. doi: 10.1016/S0893-9659(98)00046-9 [3] M. Ahues, A. Largillier and B. Limaye, Spectral Computations for Bounded Operators, Chapman and Hall/CRC, 2001. [4] C. Allouch, K. Kant and R. Nigam, Spectral projection methods for derivative dependent Hammerstein equations with Green's kernels, Mediterr. J. Math., 2024, 21(3), 48. doi: 10.1007/s00009-024-02589-1 [5] N. Anderson and A. M. Arthurs, Analytical bounding functions for diffusion problems with Michaelis-Menten kinetics, Bull. Math. Biol., 1985, 47, 145–153. doi: 10.1016/S0092-8240(85)90009-6 [6] K. E. Atkinson, The Numerical Solution of Integral Equations of the Second Kind, Cambridge University Press, 1997. [7] K. E. Atkinson and F. Potra, The discrete Galerkin method for nonlinear integral equations, J. Integral Equations Appl., 1988, 17–54. [8] K. E. Atkinson, F. Potra and A. Florian, Projection and iterated projection methods for nonlinear integral equations, SIAM J. Numer. Anal., 1987, 24(6), 1352–1373. doi: 10.1137/0724087 [9] Z. Cen, Numerical study for a class of singular two-point boundary value problems using Green's functions, Appl. Math. Comput., 2006, 183(1), 10–16. [10] S. Chakraborty and N. Gnaneshwar, Approximated superconvergent methods for Volterra Hammerstein integral equations, Commun. Nonlinear. Sci. Numer. Simulat., 2024, 130, 107783. doi: 10.1016/j.cnsns.2023.107783 [11] S. Chandrasekhar, An introduction to the study of stellar structure, Courier Corporation, 1957, 2. [12] F. Chatelin, Spectral Approximation of Linear Operators, SIAM, 2011. [13] G. Chen and J. Zhou, Boundary element methods with applications to nonlinear problems, Springer Science & Business Media, 2010, 7. [14] Z. Chen, G. Long and G. Nelakanti, The discrete multi-projection method for Fredholm integral equations of the second kind, J. Integral Equations Appl., 2007, 143–162. [15] M. Danish, S. Kumar, Shashi and S. Kumar, A note on the solution of singular boundary value problems arising in engineering and applied sciences: Use of OHAM, Computers & Chemical Engineering, 2012, 36, 57–67. [16] L. Grammont, R. P. Kulkarni and P. B. Vasconcelos, Modified projection and the iterated modified projection methods for nonlinear integral equations, J. Integral Equations Appl., 2013, 25(4). [17] B. F. Gray, The distribution of heat sources in the human head-theoretical considerations, J. Theore. Biol., 1980, 82(3), 473–476. doi: 10.1016/0022-5193(80)90250-7 [18] B. Guo, Spectral Methods and their Applications, World Scientific, 1998. [19] M. Inç and J. Evans, The decomposition method for solving of a class of singular two-point boundary value problems, Int. J. Compu. Math., 2003, 80(7), 869–882. doi: 10.1080/0020716031000087087 [20] H. Kaneko, R. D. Noren and Y. Xu, Numerical solutions for weakly singular Hammerstein equations and their superconvergence, J. Integral Equations Appl., 1992, 391–407. [21] K. Kant, P. Das, G. Nelakanti and B. V. R. Kumar, Modified Galerkin method for derivative dependent Fredholm-Hammerstein integral equations of second kind, Adv. Appl. Math. Mech., 2024. [22] K. Kant, R. Kumar, S. Chakraborty and G. Nelakanti, Discrete Galerkin and iterated discrete Galerkin methods for derivative-dependent Fredholm–Hammerstein integral equations with Green's kernel, Mediterr. J. Math., 2023, 20(5), 249. doi: 10.1007/s00009-023-02444-9 [23] J. B. Keller, Electrohydrodynamics I. The equilibrium of a charged gas in a container, Journal of Rational Mechanics and Analysis, 1956, 715–724. [24] S. A. Khuri and A. Sayfy, A novel approach for the solution of a class of singular boundary value problems arising in physiology, Math. Comp. Model., 2010, 52(3–4), 626–636. doi: 10.1016/j.mcm.2010.04.009 [25] M. Kumar and N. Singh, Modified Adomian decomposition method and computer implementation for solving singular boundary value problems arising in various physical problems, Comput. Chem. Engrg., 2010, 34(11), 1750–1760. doi: 10.1016/j.compchemeng.2010.02.035 [26] S. Kumar, Superconvergence of a collocation-type method for hummerstein equations, IMA J. Numer. Anal., 1987, 7(3), 313–313. doi: 10.1093/imanum/7.3.313 [27] S. Kumar and I. H. Sloan, A new collocation-type method for Hammerstein integral equations, Math. Comput., 1987, 48(178), 585–593. doi: 10.1090/S0025-5718-1987-0878692-4 [28] M. Mandal, K. Kant and G. Nelakanti, Convergence analysis for derivative dependent Fredholm-Hammerstein integral equations with Green's kernel, J. Comput. Appl. Math., 2020, 370, 112599. doi: 10.1016/j.cam.2019.112599 [29] M. Mandal and G. Nelakanti, Superconvergence results for weakly singular Fredholm–Hammerstein integral equations, Numer. Funct. Anal. Optim., 2019, 40(5), 548–570. doi: 10.1080/01630563.2018.1561468 [30] N. Nahid and G. Nelakanti, Discrete projection methods for Hammerstein integral equations on the half-line, Calcolo, 2020, 57(4), 37. doi: 10.1007/s10092-020-00386-2 [31] R. Nigam, N. Nahid, S. Chakraborty and G. Nelakanti, Discrete projection methods for Fredholm–Hammerstein integral equations using Kumar and Sloan technique, Calcolo, 2024, 61(2), 21. doi: 10.1007/s10092-024-00573-5 [32] B. L. Panigrahi, Error analysis of Jacobi spectral collocation methods for Fredholm-Hammerstein integral equations with weakly singular kernel, Int. J. Comput. Math., 2019, 96(6), 1230–1253. doi: 10.1080/00207160.2018.1515428 [33] Y. Rostami, A new wavelet method for solving a class of nonlinear partial integro-differential equations with weakly singular kernels, Math. Sci., 2022, 16(3), 225–235. doi: 10.1007/s40096-021-00414-4 [34] Y. Rostami, An effective computational approach based on Hermite wavelet Galerkin for solving parabolic Volterra partial integro differential equations and its convergence analysis, Math. Model. Anal., 2023, 28(1), 163–179. doi: 10.3846/mma.2023.15690 [35] Y. Rostami and K. Maleknejad, Comparison of two hybrid functions for numerical solution of nonlinear mixed partial integro-differential equations, Iranian J. Sci. and Tech., Transactions A: Science, 2022, 46(2), 645–658. doi: 10.1007/s40995-022-01277-7 [36] Y. Rostami and K. Maleknejad, The solution of the nonlinear mixed partial integro-differential equation via two-dimensional hybrid functions, Mediterr. J. Math., 2022, 19(2), 89. doi: 10.1007/s00009-022-01998-4 [37] Y. Rostami and K. Maleknejad, Approximate solution to solve singular variable-order fractional Volterra–Fredholm integral partial differential equations type defined using hybrid functions, Int. J. Comput. Math., 2024. [38] Y. Rostami and K. Maleknejad, A novel approach to solving system of integral partial differential equations based on hybrid modified block-pulse functions, Math. Methods Appl. Sci., 2024, 47(4), 5798–5818. [39] R. Singh, J. Kumar and G. Nelakanti, Numerical solution of singular boundary value problems using Green's function and improved decomposition method, J. Appl. Math. Comput., 2013, 43, 409–425. doi: 10.1007/s12190-013-0670-4 [40] R. Singh, J. Kumar and G. Nelakanti, Approximate series solution of singular boundary value problems with derivative dependence using Green's function technique, Comput. Appl. Math., 2014, 33, 451–467. doi: 10.1007/s40314-013-0074-y [41] I. H. Sloan, Polynomial interpolation and hyperinterpolation over general regions, J. Approx. Theory, 1995, 83(2), 238–254. [42] G. M. Vainikko, Galerkin's perturbation method and the general theory of approximate methods for non-linear equations, USSR Comput. Math. and Math. Phy., 1967, 7(4), 1–41. -
-
-
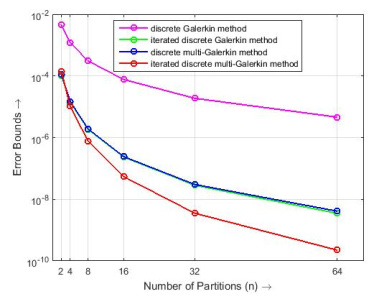
Figure 1.
Comparison of errors among proposed methods with the discrete Galerkin and iterated discrete Galerkin methods.
-
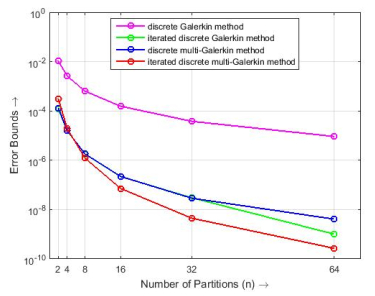
Figure 2.
Comparison of errors among proposed methods with the discrete Galerkin and iterated discrete Galerkin methods.




 DownLoad:
DownLoad: