| Citation: | Li Qiao, Ruo-Hong Li, Fan Yang, Xiao-Xiao Li. SIMULTANEOUS INVERSION OF THE SOURCE TERM AND INITIAL VALUE OF THE MULTI-TERM TIME FRACTIONAL SLOW DIFFUSION EQUATION[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 1903-1927. doi: 10.11948/20240328 |
SIMULTANEOUS INVERSION OF THE SOURCE TERM AND INITIAL VALUE OF THE MULTI-TERM TIME FRACTIONAL SLOW DIFFUSION EQUATION
-
Abstract
In this paper, the inverse problem of simultaneously identifying the source term and initial value for the multi-term time fractional diffusion equation is studied. We prove this problem is ill-posed, i.e. the solution (if it exists) does not continuous depend on measurement data. A standard Tikhonov regularization method is proposed to solve the inverse problem. In the case of a-priori and a-posteriori, we derive the error estimates between the exact solution and the regularized solution. Finally, we provide two examples to show the validity of the proposed method.
-

-
References
[1] T. S. Aleroev, M. Kirane and S. A. Malik, Determination of a source term for a time fractional diffusion equation with an integral type over-determining condiiton, Electronic Journal of Differential Equations, 2013, 2013(270), 584–609. [2] A. A. Alikhanov, A new difference scheme for the time fractional diffusion equation-ScienceDirect, Journal of Computational Physics, 2015,280(C), 424–438. [3] S. Z. Amir and S. Y. Sun, Physics-preserving averaging scheme based on Grünwald-Letnikov formula for gas flow in fractured media, Journal of Petroleum Science and Engineering, 2018,163,616–639. doi: 10.1016/j.petrol.2017.12.078 [4] M. L. Chang, L. L. Sun and Y. X. Wang, Two regularization methods for identifying the unknow source in a mulit-term time fractional diffusion equation, Rocky Mountain Journal of Mathematics, 2023, 53(5), 1387–1414. [5] M. Dehghan, M. Safarpoor and M. Abbaszadeh, Two high-order numerical algorithms for solving the multi-term time fractional diffusion-wave equations, Journal of Computational and Applied Mathematics, 2015,290,174–195. doi: 10.1016/j.cam.2015.04.037 [6] R. Gorenflo, F. Mainardi, D. Moretti, et al., Time fractional diffusion: A discrete random walk approach, Nonlinear Dynamics, 2002, 29(1–4), 129–143. [7] H. J. Haubold, A. M. Mathai and R. K. Saxena, Mittag-Leffler functions and their applications, Journal of Applied Mathematics, 2011, 2011, 36–47. [8] A. Kirsch, An Introduction to the Mathematical Theory of Inverse Problems, Springer New York, 2011. [9] Z. Li, Y. Luchko and M. Yamamoto, Asymptotic estimates of solutions to initial-boundary-value problems for distributed order time-fractional diffusion equations, Fractional Calculus Applied Analysis, 2014, 17(4), 1114–1136. doi: 10.2478/s13540-014-0217-x [10] Y. Q. Liang, F. Yang and X. X. Li, A hybrid regularization method for identifying the source term and the initial value simultaneously for fractional pseudo-parabolic equation with involution, Numerical Algorithm, 2025. DOI: 10.1007/s11075-024-01944-3. [11] J. J. Liu and M. Yamamoto, A backward problem for the time-fractional diffusion equation, Applicable Analysis, 2010, 89(11), 1769–1788. doi: 10.1080/00036810903479731 [12] Y. Luchko, Some uniqueness and existence results for the initial-boundary-value problems for the generalized time-fractional diffusion equation, Computers Mathematics with Applications, 2010, 59(5), 1766–1772. doi: 10.1016/j.camwa.2009.08.015 [13] M. D. Ortigueira and J. J. Trujillo, Generalized Grunwald-Letnikov fractional derivative and its Laplace and Fourier transforms, Journal of Computational Nonlinear Dynamics, 2011, 6(3), 34501–34503. doi: 10.1115/1.4003136 [14] I. Podlubny, Geometric and physical interpretation of fractional integration and fractional differentiation, Fractional Calculus and Applied Analysis, 2001, 5(4), 230–237. [15] I. Podlubny, Fractional Differential Equations, New York, Academic Press, 1999. [16] I. Podlubny, Fitting data using the Mittag-Leffler function, Journal of Mechanical Science and Technology, 2005, 19(11), 2016–2024. doi: 10.1007/BF02916494 [17] L. Qiao, F. Yang and X. X. Li, Simultaneous identification of the unknown source term and initial value for the time fractional diffusion equation with local and nonlocal operators, Chaos Solitons and Fractals, 2024,189, 115601. doi: 10.1016/j.chaos.2024.115601 [18] J. Ren and Z. Z. Sun, Efficient numerical solution of the multi-term time fractional diffusion-wave equation, East Asian Journal on Applied Mathematics, 2015, 5(01), 1–28. doi: 10.4208/eajam.080714.031114a [19] Z. Ruan, J. Z. Yang and X. Lu, Tikhonov regularisation method for simultaneous inversion of the source term and initial data in a time-fractional diffusion equation, East Asian Journal on Applied Mathematics, 2015, 5(03), 273–300. doi: 10.4208/eajam.310315.030715a [20] S. Shen, F. Liu and V. Anh, The analytical solution and numerical solutions for a two-dimensional multi-term time fractional diffusion and diffusion-wave equation, Journal of Computational and Applied Mathematics, 2019,345,515–534. doi: 10.1016/j.cam.2018.05.020 [21] M. Stojanovi and R. Gorenflo, Nonlinear two-term time fractional diffusion-wave problem, Nonlinear Analysis Real World Applications, 2010, 11(5), 3512–3523. doi: 10.1016/j.nonrwa.2009.12.012 [22] L. L. Sun, Y. S. Li and Y. Zhang, Simultaneous inversion of the potential term and the fractional orders in a multi-term time-fractional diffusion equation, Inverse Problems, 2021, 37(5), 055007. doi: 10.1088/1361-6420/abf162 [23] L. L. Sun, Y. Zhang and T. Wei, Recovering the time-dependent potential function in a multi-term time-fractional diffusion equation, Applied Numerical Mathematics, 2019,135,228–245. doi: 10.1016/j.apnum.2018.09.001 [24] Z. Tomovski and T. Sandev, Effects of a fractional friction with power-law memory kernel on string vibrations, Computers Mathematics with Applications, 2011, 62(3), 1554–1561. doi: 10.1016/j.camwa.2011.04.042 [25] Z. Tomovski and T. Sandev, Fractional wave equation with a frictional memory kernel of Mittag-Leffler type, Applied Mathematics and Computation, 2012,218(20), 10022–10031. doi: 10.1016/j.amc.2012.03.055 [26] T. Wei and J. Wang, Simultaneous determination for a space-dependent heat source and the initial data by the MFS, Engineering Analysis with Boundary Elements, 2012, 36(12), 1848–1855. doi: 10.1016/j.enganabound.2012.07.006 [27] F. Yang, Y. Cao and X. X. Li, Identifying source term and initial value simultaneously for the time-fractional diffusion equation with Caputo-like hyper-Bessel operator, Fractional Calculus and Applied Analysis, 2024, 27, 2359–2396. doi: 10.1007/s13540-024-00304-1 [28] F. Yang, Q. Pu and X. X. Li, The fractional Landweber method for identifying the space source term problem for time-space fractional diffusion equation, Numerical Algorithms, 2021, 87(3), 1229–1255. doi: 10.1007/s11075-020-01006-4 [29] F. Yang, L. L. Yan, H. Liu and X. X. Li, Two regularization methods for identifying the unknown source of sobolev equation with fractional Laplacian, Journal of Applied Analysis and Computation, 2025, 15(1), 198–225. [30] F. Yang, Y. Zhang and X. X. Li, Landweber iterative method for an inverse source problem of time-space fractional diffusion-wave equation, Computational Methods in Applied Mathematics, 2024, 24(1), 265–278. doi: 10.1515/cmam-2022-0240 [31] Q. Yang, D. L. Chen, T. B. Zhao and Y. Q. Chen, Fractional calculus in image processing: A review, Fractional Calculus and Applied Analysis, 2016, 19(5), 1222–1249. doi: 10.1515/fca-2016-0063 [32] C. Y. Zhang, F. Yang and X. X. Li, Two regularization methods for identifying the spatial source term problem for a space-time fractional diffusion-wave equation, Mathematics, 2024, 12,231. doi: 10.3390/math12020231 [33] Y. N. Zhang, Z. Z. Sun and H. L. Liao, Finite difference methods for the time fractional diffusion equation on non-uniform meshes, Journal of Computational Physics, 2014,265(3), 195–210. [34] G. H. Zheng and T. Wei, Two regularization methods for solving a Riesz-Feller space-fractional backward diffusion problem, Inverse Problems, 2010, 26(11), 115017. doi: 10.1088/0266-5611/26/11/115017 -
-
-
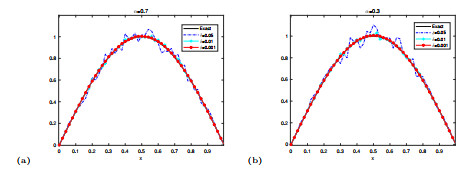
Figure 1.
The exact solution and regularized solution of the source term.
-
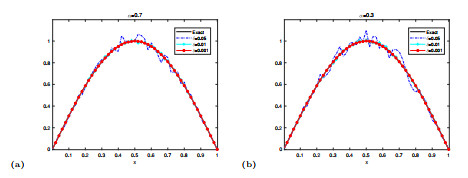
Figure 2.
The exact solution and regularized solution of the initial value.
-
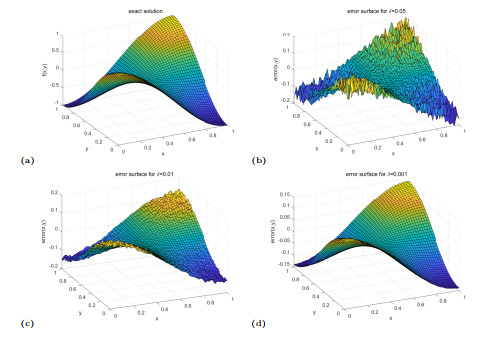
Figure 3.
The exact solution and error surface of the source term.
-
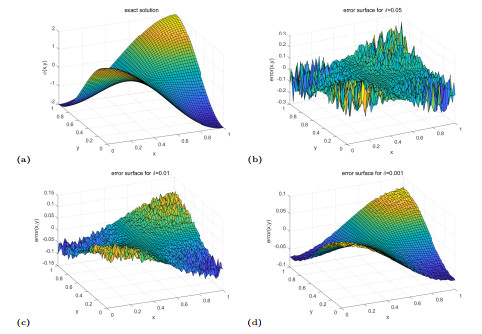
Figure 4.
The exact solution and error surface of the initial value.




 DownLoad:
DownLoad: