| Citation: | Lili Jia, Changyou Wang. STABILITY OF A NONAUTONOMOUS DELAYED PERIODIC REACTION-DIFFUSION PREDATOR-PREY MODEL[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 1928-1944. doi: 10.11948/20240332 |
STABILITY OF A NONAUTONOMOUS DELAYED PERIODIC REACTION-DIFFUSION PREDATOR-PREY MODEL
-
Abstract
This article focuses on the stability of periodic solution of a delayed nonautonomous reaction-diffusion predator-prey model. The fine combination of upper and lower solution methods and Lyapunov stability theory is used to transform the study of the stability problem of delayed reaction-diffusion equations into the stability problem of their corresponding delayed ordinary differential equations. Some sufficient conditions are given to ensure the globally asymptotically stability of the periodic solution for this model. Unlike existing results, the stable solution which are obtained in this article is a time-periodic solution rather than a constant periodic solution or a solution for a steady-state system. We extend a stability theorem on predator-prey model introduced by V. Ortega and C. Rebelo in 2023 to nonautonomous delayed reaction-diffusion model. Finally, in order to show the application of the theoretical results, the proposed conditions are numerically validated over a 2-periodic delayed nonautonomous reaction-diffusion predator-prey model.
-

-
References
[1] Z. Amine and R. Ortega, A periodic prey-predator system, Journal of Mathematical Analysis and Applications, 1994, 185, 477–489. doi: 10.1006/jmaa.1994.1262 [2] S. Bentout, S. Djilali and A. Atangana, Bifurcation analysis of an age-structured prey-predator model with infection developed in prey, Mathematical Methods in the Applied Sciences, 2021, 45(3), 1189–1208. [3] S. Bentout, S. Djilali, T. Kuniya and J. Wang, Mathematical analysis of a vaccination epidemic model with nonlocal diffusion, Mathematical Methods in the Applied Sciences, 2023, 46(9), 10970–10994. doi: 10.1002/mma.9162 [4] S. Bentouta and S. Djilalia, Asymptotic profiles of a nonlocal dispersal SIR epidemic model with treat-age in a heterogeneous environment, Mathematics and Computers in Simulation, 2023, 203, 926–956. doi: 10.1016/j.matcom.2022.07.020 [5] N. F. Britton, Reaction-Diffusion Equations and their Applications to Biology, Academic Press, New York, 1986. [6] M. X. Chen and R. C. Wu, Steady states and spatiotemporal evolution of a diffusive predator-prey model, Chaos Solitons & Fractals, 2023, 170, ID: 113397. [7] S. S. Chen and J. S. Yu, Stability and bifurcations in a nonlocal delayed reaction-diffusion population model, Journal of Differential Equations, 2016, 260, 218–240. doi: 10.1016/j.jde.2015.08.038 [8] S. Djilali, Threshold asymptotic dynamics for a spatial age-dependent cell-to-cell transmission model with nonlocal disperse, Discrete and Continuous Dynamical Systems-Series B, 2023, 28(7), 4108–4143. doi: 10.3934/dcdsb.2023001 [9] S. Djilali, Dynamics of a spatiotemporal SIS epidemic model with distinct mobility range, Applicable Analysis, 2024. DOI: 10.1080/00036811.2024.2382267. [10] S. Djilalia, Generalities on a delayed spatiotemporal host-pathogen infection model with distinct dispersal rates, Mathematical Modelling of Natural Phenomena, 2024, 19, ID: 11. doi: 10.1051/mmnp/2024008 [11] S. Djilali, S. Bentout and A. Zeb, Dynamics of a diffusive delayed viral infection model in a heterogeneous environment, Mathematical Methods in the Applied Sciences, 2023, 46(16), 16596–16624. doi: 10.1002/mma.9463 [12] S. Djilali and C. Cattani, Patterns of a superdiffusive consumer-resource model with hunting cooperation functional response, Chaos, Solitons and Fractals, 2021, 151, ID: 111258. doi: 10.1016/j.chaos.2021.111258 [13] J. K. Hale, Theory of Functional Differential Equations, Springer-Verlag, New York, 1977. [14] B. J. Huang and B. X. Dai, Spatial dynamics of a lattice Lotka-Volterra competition model with a shifting habitat, Journal of Nonlinear Modeling and Analysis, 2024, 6(1), 161–183. [15] L. L. Jia, J. Huang and C. Y. Wang, Global stability of periodic solution for a 3-species nonautonomous ratio-dependent diffusive predator-prey system, Journal of Applied Analysis and Computation, 2024, 14(4), 1–19. [16] H. K. Khalil, Nonlinear Systems, 3rd ed, Prentice-Hall, Englewood Cliffs, 2002. [17] W. Ko and I. Ahn, A diffusive one-prey and two-competing-predator system with a ratio-dependent functional response: II stationary pattern formation, Journal of Mathematical Analysis and Applications, 2013, 397(1), 29–45. doi: 10.1016/j.jmaa.2012.07.025 [18] V. Kumar, Pattern formation and delay-induced instability in a Leslie-Gower type prey-predator system with Smith growth function, Mathematics and Computers in Simulation, 2024, 225, 78–97. doi: 10.1016/j.matcom.2024.05.004 [19] Q. Li, L. Zhang and P. Zhou, Global bifurcation for a class of Lotka-Volterra competitive systems, Journal of Nonlinear Modeling and Analysis, 2023, 5(4), 720–739. [20] J. Muller and C. Kuttler, Methods and Models in Mathematical Biology: Deterministic and Stochastic Approaches, Springer, New York, 2015. [21] Y. Nakata and Y. Muroya, Permanence for nonautonomous Lotka-Volterra cooperative systems with delays, Nonlinear Analysis: Real World Applications, 2010, 11, 528–534. doi: 10.1016/j.nonrwa.2009.01.002 [22] R. Ortega, Variations on Lyapunov's stability criterion and periodic prey-predator systems, Electronic Research Archive, 2021, 29(6), 3995–4008. doi: 10.3934/era.2021069 [23] V. Ortega and C. Rebelo, A note on stability criteria in the periodic Lotka-Volterra predator-prey model, Applied Mathematics Letters, 2023, 145, ID: 10873. [24] Z. L. Shen and J. J. Wei, Spatiotemporal patterns in a delayed reaction-diffusion mussel-algae model, International Journal of Bifurcation and Chaos, 2019, 29(12), ID: 1950164. doi: 10.1142/S0218127419501645 [25] Q. Y. Shi, J. P. Shi and Y. L. Song, Hopf bifurcation in a reaction-diffusion equation with distributed delay and Dirichlet boundary condition, Journal of Differential Equations, 2017, 263, 6537–6575. doi: 10.1016/j.jde.2017.07.024 [26] C. Wang, Existence and stability of periodic solutions for parabolic systems with time delays, Journal of Mathematical Analysis and Applications, 2008, 339, 1354–1361. doi: 10.1016/j.jmaa.2007.07.082 [27] C. Wang, N. Li, Y. Zhou, X. Pu and R. Li, On a multi-delay Lotka-Volterra predator-prey model with feedback controls and prey diffusion, Acta Mathematica Scientia, Series B, 2019, 39, 429–448. doi: 10.1007/s10473-019-0209-3 [28] C. Y. Wang and Z. G. Yang, Method of Upper and Lower Solutions for Reaction Diffusion Systems with Delay, Science Press, Beijing, 2013. (in Chinese). [29] J. F. Wang, Spatiotemporal patterns of a homogeneous diffusive predator-prey system with Holling type III functional response, Journal of Dynamics and Differential Equations, 2017, 29, 1383–1409. doi: 10.1007/s10884-016-9517-7 [30] D. Y. Wu and H. Y. Zhao, Spatiotemporal dynamics of a diffusive predator-prey system with allee effect and threshold hunting, Journal of Nonlinear Science, 2020, 30, 1015–1054. doi: 10.1007/s00332-019-09600-0 [31] J. Wu, Theory and Applications of Partial Functional Differential Equations, Springer, New York, 1996. [32] W. X. Xu, H. Y. Shu, Z. Tang and H. Wang, Complex dynamics in a general diffusive predator-prey model with predator maturation delay, Journal of Dynamics and Differential Equations, 2022. DOI: 10.1007/s10884-022-10176-9. [33] X. P. Yan and C. H. Zhang, Spatiotemporal dynamics in a diffusive predator-prey system with Beddington-DeAngelis functional response, Qualitative Theory of Dynamical Systems, 2022, 21(4), ID: 166. doi: 10.1007/s12346-022-00700-z [34] W. B. Yang, Y. L. Li, J. H. Wu and H. X. Li, Dynamics of a food chain model with ratio-dependent and modified Leslie-Gower functional responses, Discrete and Continuous Dynamical Systems-Series B, 2015, 20(7), 2269–2290. doi: 10.3934/dcdsb.2015.20.2269 [35] Y. D. Yuan and Z. M. Guo, Global dynamics of a class of delayed differential systems with spatial non-locality, Journal of Differential Equations, 2023, 349, 176–235. doi: 10.1016/j.jde.2022.12.013 [36] Y. D. Yuan and Z. M. Guo, Monotone methods and stability results for nonlocal reaction-diffusion equations with time delay, Journal of Applied Analysis and Computation, 2018, 8(5), 1342–1368. [37] Y. Zhang and C. Wang, Stability analysis of n-species Lotka-Volterra almost periodic competition models with grazing rates and diffusion, International Journal of Biomathematics, 2014, 7(2), ID: 1450011. doi: 10.1142/S1793524514500119 [38] W. J. Zuo and J. P. Shi, Existence and stability of steady-state solutions of reaction-diffusion equations with nonlocal delay effect, Zeitschrift für angewandte Mathematik und Physik, 2021, 72(2), ID: 43. doi: 10.1007/s00033-021-01474-1 -
-
-
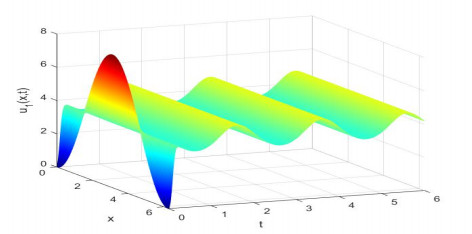
Figure 1.
Evolution process of the density for the species
$ {u_1}(x, t) $ -
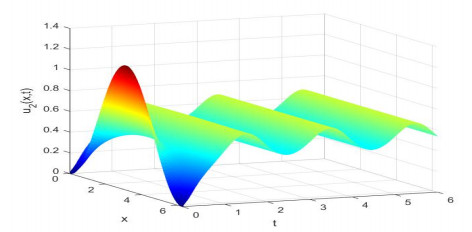
Figure 2.
Evolution process of the density for the species
$ {u_2}(x, t) $ -
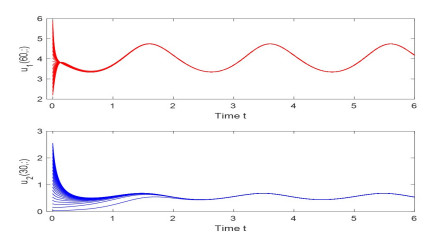
Figure 3.
Evolution process of the densities for the species
$ {u_1}(x, t) $ $ {u_2}(x, t) $




 DownLoad:
DownLoad: