| Citation: | Cheng Wang, Fei Guan, Qianqian Zhao. LIMIT CYCLES BIFURCATED FROM A KIND OF PIECEWISE SMOOTH GENERALIZED ABEL EQUATION VIA THE FIRST ORDER MELNIKOV ANALYSIS[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1695-1702. doi: 10.11948/20240338 |
LIMIT CYCLES BIFURCATED FROM A KIND OF PIECEWISE SMOOTH GENERALIZED ABEL EQUATION VIA THE FIRST ORDER MELNIKOV ANALYSIS
-
Abstract
The study of the existence and distribution of limit cycles for generalized Abel equations comes from the famous Small-Pugh problem, which has been extended to non-smooth case. In this paper, we consider a kind of piecewise smooth generalized Abel equation with the separation line $ t=0 $. We are interested in its number of nontrivial limit cycles which are bifurcated from the periodic annulus of unperturbed equation. Under the first order Melnikov analysis, we show that the upper bound of this kind nontrivial limit cycles is $ 2(m+1) $ if $ p $ is odd, and $ m+1 $ if $ p $ is even. The upper bound in both cases can be reached separately.
-

-
References
[1] M. J. Álvarez, A. Gasull and H. Giacomini, A new uniqueness criterion for the number of periodic orbits of Abel equations, J. Differential Equations, 2007, 234(1), 161–176. doi: 10.1016/j.jde.2006.11.004 [2] D. M. Benardete, V. W. Noonburg and B. Pollina, Qualitative tools for studying periodic solutions and bifurcations as applied to the periodically harvested logistic equation, Amer. Math. Monthly, 2008, 115(3), 202–219. doi: 10.1080/00029890.2008.11920518 [3] L. A. Cherkas, The number of limit cycles of a certain second order autonumous system, Differencial'nye Uravnenija, 1976, 12(5), 944–946, 960. [4] E. Fossas, J. M. Olm and H. Sira-Ramírez, Iterative approximation of limit cycles for a class of Abel equations, Phys. D, 2008, 237(23), 3159–3164. doi: 10.1016/j.physd.2008.05.011 [5] A. Gasull, Some open problems in low dimensional dynamical systems, SeMA J., 2021, 78(3), 233–269. doi: 10.1007/s40324-021-00244-3 [6] A. Gasull and A. Guillamon, Limit cycles for generalized Abel equations, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2006, 16(12), 3737–3745. doi: 10.1142/S0218127406017130 [7] A. Gasull, C. Li and J. Torregrosa, A new Chebyshev family with applications to Abel equations, J. Differential Equations, 2012, 252(2), 1635–1641. doi: 10.1016/j.jde.2011.06.010 [8] A. Gasull and J. Llibre, Limit cycles for a class of Abel equations, SIAM J. Math. Anal., 1990, 21(5), 1235–1244. doi: 10.1137/0521068 [9] M. Han, On the maximum number of periodic solutions of piecewise smooth periodic equations by average method, J. Appl. Anal. Comput., 2017, 7(2), 788–794. [10] M. Han and L. Sheng, Bifurcation of limit cycles in piecewise smooth systems via Melnikov function, J. Appl. Anal. Comput., 2015, 5(4), 809–815. [11] M. Han and J. Yang, The maximum number of zeros of functions with parameters and application to differential equations, J. Nonlinear Model. Anal., 2021, 3(1), 13–34. [12] T. Harko and M. K. Mak, Travelling wave solutions of the reaction-diffusion mathematical model of glioblastoma growth: An Abel equation based approach, Math. Biosci. Eng., 2015, 12(1), 41–69. doi: 10.3934/mbe.2015.12.41 [13] J. Huang and J. Li, On the number of limit cycles in piecewise smooth generalized Abel equations with two asymmetric zones, Nonlinear Anal. Real World Appl., 2022, 66, Paper No. 103551, 17. [14] J. Huang and H. Liang, A geometric criterion for equation $\dot x=\sum^m_{i=0}a_i(t)x^i$ having at most $m$ isolated periodic solutions, J. Differential Equations, 2020, 268(10), 6230–6250. [15] J. Huang, H. Liang and J. Llibre, Non-existence and uniqueness of limit cycles for planar polynomial differential systems with homogeneous nonlinearities, J. Differential Equations, 2018, 265(9), 3888–3913. [16] J. Huang and Z. Peng, Bifurcation of a kind of piecewise smooth generalized Abel equation via first and second order analyses, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2020, 30(16), 2050247, 20. [17] J. Huang, J. Torregrosa and J. Villadelprat, On the number of limit cycles in generalized Abel equations, SIAM J. Appl. Dyn. Syst., 2020, 19(4), 2343–2370. [18] J. Huang and Y. Zhao, Periodic solutions for equation $\dot x=A(t)x^m+B(t)x^n+C(t)x^l$ with $A(t)$ and $B(t)$ changing signs, J. Differential Equations, 2012, 253(1), 73–99. [19] M. Krusemeyer, The teaching of mathematics: Why does the wronskian work?, Amer. Math. Monthly, 1988, 95(1), 46–49. [20] C. J. Liu and S. Q. Wang, On the center problem for generalized Abel equations, Acta Math. Sin. (Engl. Ser.), 2023, 39(12), 2329–2337. [21] N. G. Lloyd, The number of periodic solutions of the equation $\dot z=z^{N}+p_{1}(t)z^{N-1}+...+p_{N}(t)$, Proc. London Math. Soc. (3), 1973, 27, 667–700. $\dot z=z^{N}+p_{1}(t)z^{N-1}+...+p_{N}(t)$" target="_blank">Google Scholar
[22] N. G. Lloyd, On a class of differential equations of Riccati type, J. London Math. Soc. (2), 1975, 10, 1–10. [23] N. G. Lloyd, A note on the number of limit cycles in certain two-dimensional systems, J. London Math. Soc. (2), 1979, 20(2), 277–286. [24] A. Lins Neto, On the number of solutions of the equation $dx/dt=\sum ^{n}_{j=0} a_{j}(t)x^{j}$, $0\leq t\leq 1$, for which $x(0)=x(1)$, Invent. Math., 1980, 59(1), 67–76. [25] A. A. Panov, Variety of Poincaré mappings for cubic equations with variable coefficients, Funktsional. Anal. i Prilozhen., 1999, 33(4), 84–88. [26] S. Smale, Mathematical problems for the next century, in Mathematics: Frontiers and perspectives, Amer. Math. Soc., Providence, RI, 2000, 271–294. [27] R. Tian and Y. Zhao, On the number of limit cycles in piecewise smooth generalized Abel equations with many separation lines, Nonlinear Anal. Real World Appl., 2024, 80, Paper No. 104151. [28] Y. Tian, X. Shang and M. Han, Bifurcation of limit cycles in a piecewise smooth near-integrable system, J. Math. Anal. Appl., 2021, 504(2), Paper No. 125578, 11. [29] X. Yu, J. Huang and C. Liu, Maximum number of limit cycles for Abel equation having coefficients with linear trigonometric functions, J. Differential Equations, 2024, 410, 301–318. [30] Q. Zhao, J. Yu and C. Wang, Nontrivial limit cycles in a kind of piecewise smooth generalized Abel equation, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2022, 32(14), Paper No. 2250216, 18. -
-
-
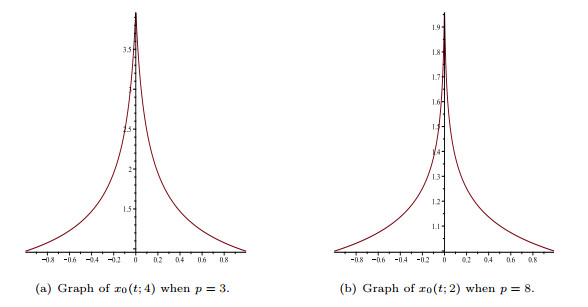
Figure 1.
Graphs of
$ x_0(t;\rho) $ $ \rho $ $ p $ -
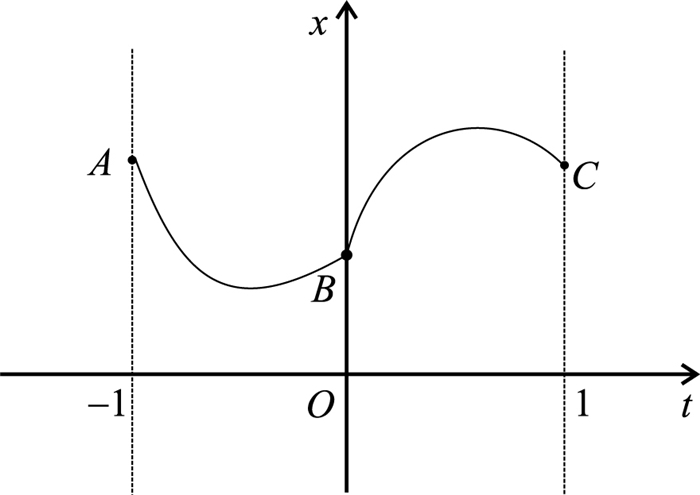
Figure 2.
Illustration of flow
$ x_\varepsilon(t;\rho) $ $ A\rightarrow B \rightarrow C $




 DownLoad:
DownLoad: