| Citation: | Nurullah Yilmaz. A NEW SMOOTHING FUNCTION TECHNIQUE FOR SOLVING MINIMAX PROBLEMS[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1703-1718. doi: 10.11948/20240361 |
A NEW SMOOTHING FUNCTION TECHNIQUE FOR SOLVING MINIMAX PROBLEMS
-
Abstract
In this study, we consider non-smooth finite minimax problems. A new approach for solving minimax problems is developed, employing indicator functions and smoothing functions. First, the formulation of minimax problems is revised using indicator functions. Then, a new generation smoothing technique is used for the revised formulation. An algorithm is developed to solve the revised and smoothed problems numerically. The efficiency of the algorithm is demonstrated on several test problems, and a comparison is conducted between the numerical results achieved and those of alternative approaches. Finally, the portfolio planning problem is considered as a real-life application, and satisfactory results are obtained.
-
Keywords:
- Minimax problem /
- non-smooth optimization /
- smoothing technique
-

-
References
[1] T. Antczak, The minimax exact penalty fuzzy function method for solving convex nonsmooth optimization problems with fuzzy objective functions, J. Ind. Manag. Optim., 2024, 20(1), 392–427. doi: 10.3934/jimo.2023083 [2] E. M. Arkin, R. Hassin and A. Levin, Approximations for minimum and min-max vehicle routing problems, J. Algorithm., 2006, 59(1), 1–18. doi: 10.1016/j.jalgor.2005.01.007 [3] A. Bagirov, A. A. Nuaimat and N. Sultanova, Hyperbolic smoothing function method for minimax problems, Optimization, 2013, 62(6), 759–782. doi: 10.1080/02331934.2012.675335 [4] A. M. Bagirov, N. Sultanova, A. Al Nuaimat and S. Taheri, Solving minimax problems: Local smoothing versus global smoothing, in Numerical Analysis and Optimization (Edited by M. Al-Baali, L. Grandinetti and A. Purnama), Springer International Publishing, Cham, 2018, 23–43. [5] D. P. Bertsekas, On penalty and multiplier methods for constrained minimization, SIAM J. Control Optim., 1976, 14(2), 216–235. doi: 10.1137/0314017 [6] X. Cai, K. -L. Teo, X. Yang and X. Y. Zhou, Portfolio optimization under a minimax rule, Manag. Sci., 2000, 46(7), 957–972. [7] C. Chen and O. L. Mangasarian, A class of smoothing functions for nonlinear and mixed complementarity problems, Comput. Optim. Appl., 1996, 5(2), 97–138. doi: 10.1007/BF00249052 [8] X. Chen, Smoothing methods for nonsmooth, nonconvex minimization, Math. Programm., 2012, 134(1), 71–99. doi: 10.1007/s10107-012-0569-0 [9] V. F. Demyanov and V. N. Malozemov, Introduction Minimax, Wiley, New York, 1974. [10] L. Dong and B. Yu, A spline smoothing newton method for finite minimax problems, J. Eng. Math., 2015, 93(1), 145–158. doi: 10.1007/s10665-014-9733-2 [11] D. Z. Du and P. M. Pardalos, Minimax and Applications, 4, Kluwer Academic, Dordrecht, 1995. [12] J. Du, L. Zhao, J. Feng and X. Chu, Computation offloading and resource allocation in mixed fog/cloud computing systems with min-max fairness guarantee, IEEE Trans. Commun., 2018, 66(4), 1594–1608. doi: 10.1109/TCOMM.2017.2787700 [13] T. Ergenc, S. W. Pickl, N. Radde and G. W. Weber, Generalized semi-infinite optimization and anticipatory systems, International Journal of Computing Anticipatory Systems, 2004, 15, 3–30. [14] W. Fan, J. Liang, H. C. So and G. Lu, Min-max metric for spectrally compatible waveform design via log-exponential smoothing, IEEE Trans. Signal Process., 2020, 68, 1075–1090. doi: 10.1109/TSP.2020.2969043 [15] Y. Feng, L. Hongwei, Z. Shuisheng and L. Sanyang, A smoothing trust-region newton-cg method for minimax problem, Appl. Math. Comput., 2008, 199(2), 581–589. [16] A. Fuduli, M. Gaudioso, G. Giallombardo and G. Miglionico, A partially inexact bundle method for convex semi-infinite minmax problems, Commun. Nonlinear Sci. Numer. Simul., 2015, 21(1), 172–180. Numerical Computations: Theory and Algorithms (NUMTA 2013), International Conference and Summer School. [17] M. Gaudioso, G. Giallombardo and G. Miglionico, An incremental method for solving convex finite min-max problems, Math. Oper. Res., 2006, 31(1), 173–187. doi: 10.1287/moor.1050.0175 [18] C. Grossman, Smoothing techniques for exact penalty function methods, American Mathematical Society, Providence, Rhode Island, 2016, 249–265. [19] Z. Cobandag Guloglu and G. W. Weber, Risk modeling in optimization problems via value at risk, conditional value at risk, and its robustification, in Modeling, Dynamics, Optimization and Bioeconomics Ⅱ (Edited by A. A. Pinto and D. Zilberman), Springer International Publishing, Cham., 2017, 133–145. [20] H. T. Jongen and O. Stein, Smoothing by mollifiers, part i: Semi-infinite optimization, J. Global Optim., 2008, 41, 319–334. doi: 10.1007/s10898-007-9232-3 [21] H. T. Jongen and O. Stein, Smoothing by mollifiers, part ii: Nonlinear optimization, J. Global Optim., 2008, 41, 335–350. doi: 10.1007/s10898-007-9231-4 [22] H. T. Jongen, F. Twilt and G. W. Weber, Semi-infinite optimization: Structure and stability of the feasible set, J. Optim. Theory Appl., 1992, 72, 529–552. doi: 10.1007/BF00939841 [23] J. Liu and L. Zheng, A smoothing iterative method for the finite minimax problem, J. Comput. Appl. Math., 2020, 374, 112741. doi: 10.1016/j.cam.2020.112741 [24] L. Luksan and J. Vlcek, Test problems for non-smooth unconstrained and linearly constrained optimization, Technical Reports No. 798, Institute of Computer Science, Academy of Sciences of the Czech Republic, 2000. [25] S. Mahmoudinazlou and C. Kwon, A hybrid genetic algorithm for the min–max multiple traveling salesman problem, Comput. Oper. Res., 2024, 162, 106455. doi: 10.1016/j.cor.2023.106455 [26] A. Nezami and M. Mortezaee, A new gradient-based neural dynamic framework for solving constrained min-max optimization problems with an application in portfolio selection model, Appl. Intell., 2019, 49(2), 369–419. [27] A. Özmen, E. Kropat and G. -W. Weber, Robust optimization in spline regression models for multi-model regulatory networks under polyhedral uncertainty, Optimization, 2017, 66(12), 2135–2155. doi: 10.1080/02331934.2016.1209672 [28] B. Akteke-Öztürk, G. -W. Weber and G. Köksal, Optimization of generalized desirability functions under model uncertainty, Optimization, 2017, 66(12), 2157–2169. doi: 10.1080/02331934.2017.1371167 [29] B. Akteke-Öztürk, G. -W. Weber and G. Köksal, Generalized desirability functions: A structural and topological analysis of desirability functions, Optimization, 2020. [30] C. Papahristodoulou and E. Dotzauer, Optimal portfolios using linear programming models, J. Oper. Res. Soc., 2004, 55(11), 1169–1177. doi: 10.1057/palgrave.jors.2601765 [31] E. Polak, On the mathematical foundations of nondifferentiable optimization in engineering design, SIAM Review, 1987, 29(1), 21–89. doi: 10.1137/1029002 [32] E. Polak, J. O. Royset and R. S. Womersley, Algorithms with adaptive smoothing for finite minimax problems, J. Optim. Theory Appl., 2003, 119(3), 459–484. doi: 10.1023/B:JOTA.0000006685.60019.3e [33] A. Sahiner, G. Kapusuz and N. Yilmaz, A new smoothing approach to exact penalty functions for inequality constrained optimization problems, Numer. Algebra Control Optim., 2016, 6(2), 161–173. doi: 10.3934/naco.2016006 [34] W. Sánchez, C. Arias and R. Perez, A jacobian smoothing inexact newton method for solving the nonlinear complementary problem, Comput. Appl. Math., 2024, 43(5), 279. doi: 10.1007/s40314-024-02775-7 [35] M. Souza, A. E. Xavier, C. Lavor and N. Maculan, Hyperbolic smoothing and penalty techniques applied to molecular structure determination, Oper. Res. Lett., 2011, 39(6), 461–465. doi: 10.1016/j.orl.2011.07.007 [36] K. L. Teo and X. Yang, Portfolio selection problem with minimax type risk function, Ann. Oper. Res., 2001, 101, 333–349. doi: 10.1023/A:1010909632198 [37] F. Guerra Vazquez, H. Günzel and H. Jongen, On logarithmic smoothing of the maximum function, Ann. Oper. Res., 2001, 101(1), 209–220. [38] H. Wang, A decentralized smoothing quadratic regularization algorithm for composite consensus optimization with non-lipschitz singularities, Numer. Algorithm., 2024, 96(1), 369–396. doi: 10.1007/s11075-023-01650-6 [39] A. E. Xavier, The hyperbolic smoothing clustering method, Pattern Recogn., 2010, 43(3), 731–737. doi: 10.1016/j.patcog.2009.06.018 [40] S. Xu, Smoothing method for minimax problems, Comput. Optim. Appl., 2001, 20(3), 267–279. doi: 10.1023/A:1011211101714 [41] N. Yilmaz and A. Kayacan, A new smoothing algorithm to solve a system of nonlinear inequalities, Fundamental Journal of Mathematics and Applications, 2023, 6(3), 137–146. doi: 10.33401/fujma.1261409 [42] N. Yilmaz and A. Sahiner, New smoothing approximations to piecewise smooth functions and applications, Numer. Funct. Anal. Optim., 2019, 40(5), 513–534. doi: 10.1080/01630563.2018.1561466 [43] N. Yilmaz and A. Sahiner, Smoothing techniques in solving non-lipschitz absolute value equations, Int. J. Comput. Math., 2023, 100(4), 867–879. doi: 10.1080/00207160.2022.2163388 [44] H. Yin, An adaptive smoothing method for continuous minimax problems, Asia-Pac. J. Oper. Res., 2015, 32(01), 1540001. doi: 10.1142/S0217595915400011 [45] I. Zang, A smoothing-out technique for min–max optimization, Math. Programm., 1980, 19(1), 61–77. [46] Z. Zhou and Y. Duan, An aggregate homotopy method for solving unconstrained minimax problems, Optimization, 2021, 70(8), 1791–1808. [47] Z. Zhou and Q. Yang, An active set smoothing method for solving unconstrained minimax problems, Math. Probl. Eng., 2020, 2020, 9108150. -
-
-
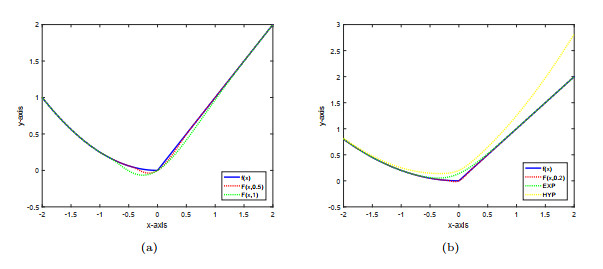
Figure 1.
(a) The blue graph is the graph of
$ f(x) $ $ \tilde{F}(x, 0.5) $ $ \tilde{F}(x, 1) $ $ f(x) $ $ \tilde{F}(x, 0.2) $ $ \varepsilon=0.2 $ $ \varepsilon=0.2 $




 DownLoad:
DownLoad: