| Citation: | Raymond Kitengeso, Zhoushun Zheng. A CONVERGENT NUMERICAL APPROXIMATION FOR THE COUPLED MAXWELL-LANDAU-LIFSHITZ-GILBERT EQUATIONS WITH INERTIA EFFECTS[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1719-1741. doi: 10.11948/20240364 |
A CONVERGENT NUMERICAL APPROXIMATION FOR THE COUPLED MAXWELL-LANDAU-LIFSHITZ-GILBERT EQUATIONS WITH INERTIA EFFECTS
-
Abstract
This study aims to analyze the coupled finite element and boundary element (FEM-BEM) solution to the nonlinear system of Maxwell and inertia Landau–Lifshitz–Gilbert equations. An algorithm is proposed to numerically solve the weak form of this problem, which requires solving coupled linear systems per time step. The algorithm is coupled in the sense that it consists of the sequential computation of the magnetic and electric fields in both the interior and boundary domains, and magnetization afterward. Under some mild assumptions on the effective field, the findings show that the algorithm converges towards a weak solution of the Maxwell-Inertia Landau–Lifshitz–Gilbert system. Numerical experiments demonstrate the algorithm's applicability for a theoretical micromagnetic example.
-
Keywords:
- Maxwell /
- Landau–Lifshitz–Gilbert /
- convergence /
- FEM-BEM
-

-
References
[1] G. Akrivis, M. Feischl, B. Kovács and C. Lubich, Higher-order linearly implicit full discretization of the Landau–Lifshitz–Gilbert equation, Math. Comput., 2021, 90(329), 995–1038. doi: 10.1090/mcom/3597 [2] M. S. Alnæs, A. Logg, K. B. Ølgaard, M. E. Rognes and G. N. Wells, Unified form language, ACM Trans. Math. Softw., 2014, 40, 1–37. [3] S. Bartels, Stability and convergence of finite-element approximation schemes for harmonic maps, SIAM J. Numer. Anal., 2005, 43(1), 220–238. doi: 10.1137/040606594 [4] T. Betcke and M. W. Scroggs, Bempp-cl: A fast python based just-in-time compiling boundary element library, J. Open Source Softw., 2021, 6, 2879. doi: 10.21105/joss.02879 [5] J. Bohn, M. Feischl and B. Kovács, Fem-bem coupling for the Maxwell–Landau–Lifshitz–Gilbert equations via convolution quadrature: Weak form and numerical approximation, Comput. Methods Appl. Math., 2023, 23, 19–48. doi: 10.1515/cmam-2022-0145 [6] Y. Cai, J. Chen, C. Wang and C. Xie, Error analysis of a linear numerical scheme for the landau–lifshitz equation with large damping parameters, Math. Meth. Appl. Sci., 2023, 46(18), 18952–18974. doi: 10.1002/mma.9601 [7] Y. Cai, J. Chen, C. Wang and C. Xie, A second-order numerical method for Landau-Lifshitz-Gilbert equation with large damping parameters, J. Comput. Phys., 2022, 451, 110831. doi: 10.1016/j.jcp.2021.110831 [8] J. Chen, C. Wang and C. Xie, Convergence analysis of a second-order semi-implicit projection method for Landau-Lifshitz equation, Appl. Numer. Math., 2021, 168, 55–74. doi: 10.1016/j.apnum.2021.05.027 [9] I. Cimrák, Existence, regularity and local uniqueness of the solutions to the Maxwell–Landau–Lifshitz system in three dimensions, J. Math. Anal. Appl., 2007, 329, 1080–1093. doi: 10.1016/j.jmaa.2006.06.080 [10] M. C. Ciornei, J. M. Rubí and J. E. Wegrowe, Magnetization dynamics in the inertial regime: Nutation predicted at short time scales, Phys. Rev. B, 2011, 83, 020410. doi: 10.1103/PhysRevB.83.020410 [11] D. Colton and R. Kress, Boundary-value problems for the time-harmonic Maxwell equations and the vector Helmholtz equation, Integral Equation Methods in Scattering Theory, SIAM, USA, 2013, Ch. 4, 108–149. [12] M. Feischl and T. Tran, Existence of regular solutions of the Landau–Lifshitz–Gilbert equation in $3d$ with natural boundary conditions, SIAM J. Math. Anal., 2017, 49, 4470–4490. doi: 10.1137/16M1103427 CrossRef $3d$ with natural boundary conditions" target="_blank">Google Scholar
[13] A. François, K. Evaggelos and T. Jean-Christophe, A convergent finite element approximation for Landau–lifschitz–Gilbert equation, Physica B, 2012, 407(9), 1345–1349. doi: 10.1016/j.physb.2011.11.031 [14] G. D. Fratta, M. Innerberger and D. Praetorius, Weak–strong uniqueness for the Landau–Lifshitz–Gilbert equation in micromagnetics, Nonlinear Anal. -Real World Appl., 2020, 55, 103122. doi: 10.1016/j.nonrwa.2020.103122 [15] B. Goldys, K. N. Le and T. Tran, A finite element approximation for the stochastic Landau–Lifshitz–Gilbert equation, J. Differ. Equ., 2016, 260(2), 937–970. doi: 10.1016/j.jde.2015.09.012 [16] E. Kim and K. Lipnikov, The mimetic finite difference method for the Landau–Lifshitz equation, J. Comput. Phys., 2017, 328, 109–130. doi: 10.1016/j.jcp.2016.10.016 [17] B. Kovács and C. Lubich, Stable and convergent fully discrete interior–exterior coupling of Maxwell's equations, Numer. Math., 2017, 137(91), 117–137. [18] M. Lakshmanan, The fascinating world of the Landau–Lifshitz–Gilbert equation: An overview, Philos. Trans. R. Soc. Lond. Ser. A-Math. Phys. Eng. Sci., 2011, 369, 1280–1300. [19] K. N. Le and T. Tran, A convergent finite element approximation for the quasi-static Maxwell–Landau–Lifshitz–Gilbert equations, Comput. Math. Appl., 2013, 66(8), 1389–1402. doi: 10.1016/j.camwa.2013.08.009 [20] B. Li, J. Wang and L. Xu, A convergent linearized lagrange finite element method for the magneto-hydrodynamic equations in two-dimensional nonsmooth and nonconvex domains, SIAM J. Numer. Anal., 2020, 58, 430–459. doi: 10.1137/18M1205649 [21] K. Neeraj, N. Awari, S. Kovalev, D. Polley, N. Zhou Hagström, S. S. P. K. Arekapudi, A. Semisalova, K. Lenz, B. Green, J. C. Deinert, I. Ilyakov, M. Chen, M. Bawatna, V. Scalera, M. d'Aquino, C. Serpico, O. Hellwig, J. E. Wegrowe, M. Gensch and S. Bonetti, Inertial spin dynamics in ferromagnets, Nat. Phys., 2021, 1, 245–250. [22] M. Ruggeri, Numerical analysis of the Landau–Lifshitz–Gilbert equation with inertial effects, ESAIM-Math. Model. Numer. Anal., 2022, 56, 1199–1222. doi: 10.1051/m2an/2022043 [23] M. W. Scroggs, T. Betcke, E. Burman, W. Śmigaj and E. van't Wout, Software frameworks for integral equations in electromagnetic scattering based on calderón identities, Comput. Math. Appl., 2017, 74(11), 2897–2914. doi: 10.1016/j.camwa.2017.07.049 [24] C. Xie, C. J. García-Cervera, C. Wang, Z. Zhou and J. Chen, Second-order semi-implicit projection methods for micromagnetics simulations, J. Comput. Phys., 2020, 404, 109104. doi: 10.1016/j.jcp.2019.109104 [25] P. Zhong, F. Wu and S. Tang, Renormalization for the laplacian and global well-possness of the Landau–Lifshitz–Gilbert equation in dimensions $n \geq3$, Bound. Value Probl., 2020, 2020, 96. doi: 10.1186/s13661-020-01377-6 -
-
-
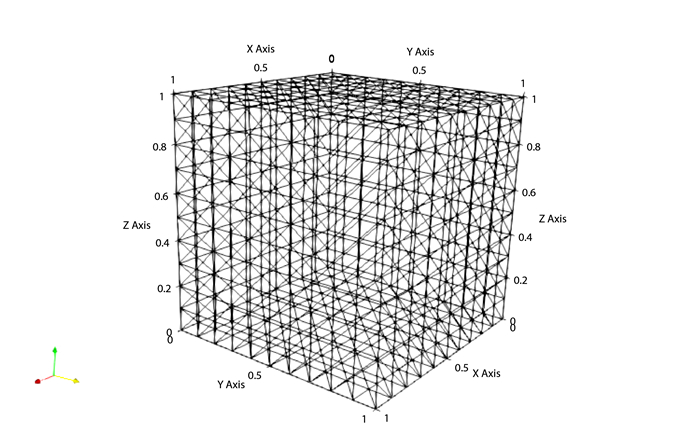
Figure 1.
The representation of cube tetrahedral mesh with a total of 3996 nodes in the domain (left) and cube surface with edges representation (right).
-
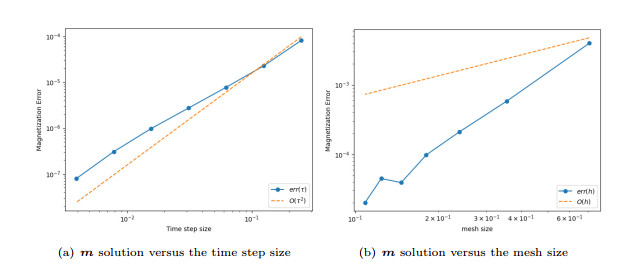
Figure 2.
Experimental error of magnetization
$ \boldsymbol{{m}} $ -
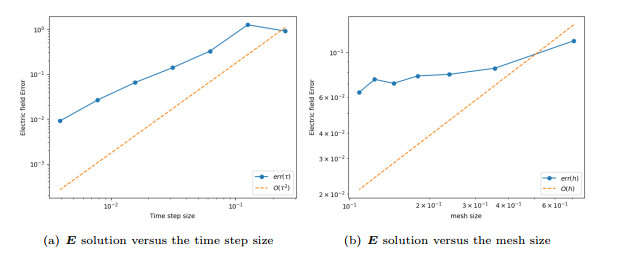
Figure 3.
Experimental error of electric field
$ \boldsymbol{{E}} $ -
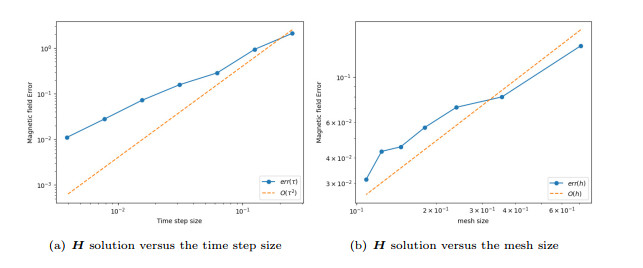
Figure 4.
Experimental error of magnetic field
$ \boldsymbol{{H}} $ -
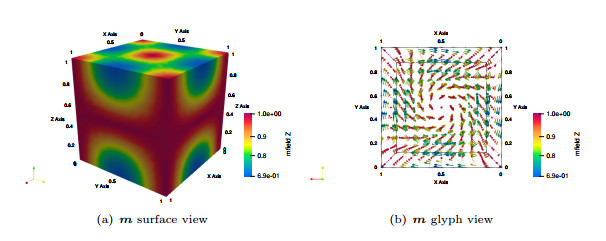
Figure 5.
The vectors in the plots denote the magnetization solution components, and the color denotes the
$ \boldsymbol{{m}}_{z} $ $ z $ -
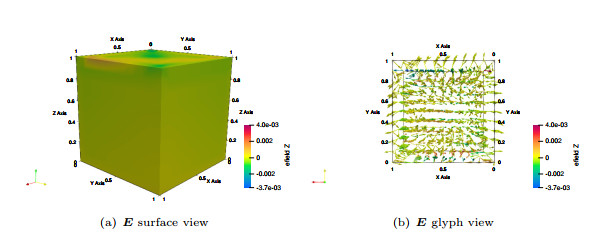
Figure 6.
The vectors in the plots denote the electric field solution components, and the color denotes the
$ \boldsymbol{{E}}_{z} $ $ z $ -
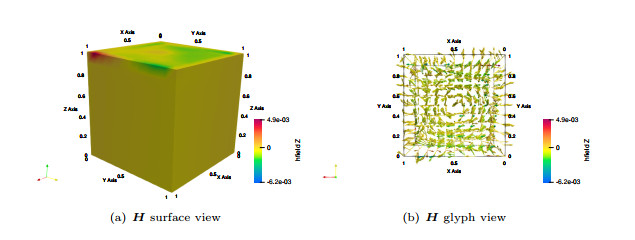
Figure 7.
The vectors in the plots denote the magnetic field solution components, and the color denotes the
$ \boldsymbol{{H}}_{z} $ $ z $




 DownLoad:
DownLoad: