| Citation: | Ji Li, Qing Yu, Qian Zhang. UNFOLDING A HOPF BIFURCATION IN A LINEAR REACTION-DIFFUSION EQUATION WITH STRONGLY LOCALIZED IMPURITY[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1742-1769. doi: 10.11948/20240379 |
UNFOLDING A HOPF BIFURCATION IN A LINEAR REACTION-DIFFUSION EQUATION WITH STRONGLY LOCALIZED IMPURITY
-
Abstract
This paper presents a general framework to derive the weakly nonlinear stability near a Hopf bifurcation in a special class of multi-scale reaction-diffusion equations. The main focus is on how the linearity and nonlinearity of the fast variables in system influence the emergence of the breathing pulses when the slow variables are linear and the bifurcation parameter is around the Hopf bifurcation point. By applying the matching principle to the fast and slow changing quantities and using the singular perturbation theory, we obtain explicit expressions for the stationary pulses. Then, the normal form theory and the center manifold theory are applied to give Hopf normal form expressions. Finally, one of these expressions is verified by the numerical simulation.
-
Keywords:
- Pinned solution /
- Hopf bifurcation /
- breathing pulse /
- center manifold expansion /
- normal form
-

-
References
[1] M. Argentina and P. Coullet, Chaotic nucleation of metastable domains, Phys. Rev. E., 1997, 56(3), R2359. doi: 10.1103/PhysRevE.56.R2359 [2] R. Bastiaansen, P. Carter and A. Doelman, Stable planar vegetation stripe patterns on sloped terrain in dryland ecosystems, Nonlinearity, 2019, 32, 2759–2814. doi: 10.1088/1361-6544/ab1767 [3] P. C. Bressloff and S. E. Folias, Front bifurcations in an excitatory neural network, SIAM J. Appl. Math., 2004, 65(1), 131–151. doi: 10.1137/S0036139903434481 [4] P. C. Bressloff, S. E. Folias, A. Prat and Y. X. Li, Oscillatory waves in inhomogeneous neural media, Phys. Rev. Lett., 2003, 91(17), 178101. doi: 10.1103/PhysRevLett.91.178101 [5] P. C. Bressloff and Z. P. Kilpatrick, Two-dimensional bumps in piecewise smooth neural fields with synaptic depression, SIAM J. Appl. Math., 2011, 71(2), 379–408. doi: 10.1137/100799423 [6] P. Carter and A. Doelman, Traveling stripes in the Klausmeier model of vegetation pattern formation, SIAM J. Appl. Math., 2018, 78(6), 3213–3237. doi: 10.1137/18M1196996 [7] W. Chen and M. J. Ward, Oscillatory instabilities and dynamics of multi-spike patterns for the one-dimensional Gray-Scott model, Eur. J. Appl. Math., 2009, 20(2), 187–214. doi: 10.1017/S0956792508007766 [8] W. Chen and M. J. Ward, The stability and dynamics of localized spot patterns in the two-dimensional Gray-Scott model, SIAM J. Appl. Dyn. Syst., 2011, 10(2), 582–666. doi: 10.1137/09077357X [9] Y. X. Chen, J. Li, J. H. Shen and Q. Zhang, Pattern formations in nonlinear reaction-diffusion systems with strong localized impurities, J. Diff. Eqs., 2024, 402, 250–289. doi: 10.1016/j.jde.2024.05.004 [10] M. Chirilus, P. van Heijster, H. Ikeda and J. D. Rademacher, Unfolding symmetric Bogdanov–Takens bifurcations for front dynamics in a reaction–diffusion system, J. Nonlinear Sci., 2019, 29, 2911–2953. doi: 10.1007/s00332-019-09563-2 [11] S. Coombes, P. B. Graben, R. Potthast and J. Wright, Neural Fields: Theory and Applications, Springer, 2014. [12] A. Doelman, P. van Heijster and J. H. Shen, Pulse dynamics in reaction–diffusion equations with strong spatially localized impurities, Philos. Trans. Roy. Soc. A, 2018, 376, 1–20. [13] A. Doelman, T. J. Kaper and K. Promislow, Nonlinear asymptotic stability of the semistrong pulse dynamics in a regularized Gierer-Meinhardt model, SIAM J. Math. Anal., 2007, 38(6), 1760–1787. doi: 10.1137/050646883 [14] A. Doelman, T. J. Kaper and P. A. Zegeling, Pattern formation in the one-dimensional Gray-Scott model, Nonlinearity, 1997, 10(2), 523. doi: 10.1088/0951-7715/10/2/013 [15] F. Dumortier, R. Roussarie and J. Sotomayor, Generic 3-parameter families of vector fields on the plane, unfolding a singularity with nilpotent linear part, the cusp case of codimension 3, Ergodic Theory Dynam. Systems, 1987, 7(3), 375–413. doi: 10.1017/S0143385700004119 [16] M. Eslami, M. Kanafchian and G. Oppo, Oscillatory and chaotic regimes of patterns and dark cavity solitons in cavities displaying EIT: Static multihead dual chimera states, Chaos Solitons Fractals, 2023, 167, 113080. doi: 10.1016/j.chaos.2022.113080 [17] S. J. Fan, A new extracting formula and a new distinguishing means on the one variable cubic equation, Natur. Sci. J. Hainan Teacheres College, 1989, 2, 91–98. [18] W. J. Firth, G. K. Harkness, A. Lord, J. M. McSloy, D. Gomila and P. Colet, Dynamical properties of two-dimensional Kerr cavity solitons, J. Opti. Soc. Amer. B-Opti. Phys., 2002, 19, 747–752. doi: 10.1364/JOSAB.19.000747 [19] S. E. Folias and P. C. Bressloff, Breathing pulses in an excitatory neural network, SIAM J. Appl. Dyn. Syst., 2004, 3(3), 378–407. doi: 10.1137/030602629 [20] S. E. Folias and P. C. Bressloff, Stimulus-locked traveling waves and breathers in an excitatory neural network, SIAM J. Appl. Math., 2005, 65(6), 2067–2092. doi: 10.1137/040615171 [21] A. Gierer and H. Meinhardt, A theory of biological pattern formation, Kybernetik, 1972, 12, 30–39. doi: 10.1007/BF00289234 [22] D. Gomila, P. Colet, M. A. Matías, G. L. Oppa and M. S. Miguel, Localized structures in nonlinear optical cavities, Topical Problems of Nonlinear Wave Physics, SPIE., 2006, 5975. [23] S. S. Gopalakrishnan, M. Tlidi, M. Taki and K. Panajotov, Breathing of dissipative light bullets of nonlinear polarization mode in Kerr resonators, Optics Letters, 2022, 47(15), 3652–3655. doi: 10.1364/OL.455758 [24] P. Gray and S. K. Scott, Autocatalytic reactions in the isothermal, continuous stirred tank reactor: Isolas and other forms of multistability, Chem. Eng. Sci., 1983, 38(1), 29–43. doi: 10.1016/0009-2509(83)80132-8 [25] S. V. Gurevich, S. Amiranashvili and H. G. Purwins, Breathing dissipative solitons in three-component reaction-diffusion system, Phys. Rev. E., 2006, 74(6), 066201. doi: 10.1103/PhysRevE.74.066201 [26] M. Haragus and G. Iooss, Local Bifurcations, Center Manifolds, and Normal Forms in Infinite-Dimensional Dynamical Systems, London, Springer, 2011. [27] C. K. R. T. Jones, Geometric singular perturbation theory, Dynamical Systems: Lectures Given at the 2nd Session of the Centro Internazionale Matematico Estivo (CIME) Held in Montecatini Terme, Italy, June 13šC22, 1995, 1994, 44–118. [28] T. Kapitula and K. Promislow, Spectral and Dynamical Stability of Nonlinear Waves, New York, Springer, 2013. [29] S. Koga and Y. Kuramoto, Localized patterns in reaction-diffusion systems, Prog. Theor. Phys., 1980, 63(1), 106–121. doi: 10.1143/PTP.63.106 [30] Y. A. Kuznetsov, I. A. Kuznetsov and Y. Kuznetsov, Elements of Applied Bifurcation Theory, Vol. 112. New York, Springer, 1998. [31] J. Li, J. H. Shen and Q. Zhang, Pinned pulses in nonlinear reaction-diffusion equations with strong localized impurities, Internat. J. Bifur. Chaos, accepted. [32] A. L. Shil'Nikov, L. P. Shil'Nikov and D. V. Turaev, Normal forms and Lorenz attractors, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 1993, 3(5), 1123–1139. doi: 10.1142/S0218127493000933 [33] D. Turaev, A. G. Vladimirov and S. Zelik, Long-range interaction and synchronization of oscillating dissipative solitons, Phys. Rev. Lett., 2012, 108(26), 263906. doi: 10.1103/PhysRevLett.108.263906 [34] F. Veerman, Breathing pulses in singularly perturbed reaction-diffusion systems, Nonlinearity, 2015, 28(7), 2211. doi: 10.1088/0951-7715/28/7/2211 [35] F. Veerman and A. Doelman, Pulses in a Gierer-Meinhardt equation with a slow nonlinearity, SIAM J. Appl. Dyn. Syst., 2013, 12(1), 28–60. doi: 10.1137/120878574 [36] A. G. Vladimirov, S. V. Fedorov, N. A. Kaliteevskii, G. V. Khodova and N. N. Rosanov, Numerical investigation of laser localized structures, Journal of Optics B: Quantum and Semiclassical Optics, 1999, 1(1), 101. doi: 10.1088/1464-4266/1/1/019 [37] M. J. Ward and J. Wei, Hopf bifurcations and oscillatory instabilities of spike solutions for the one-dimensional Gierer-Meinhardt model, J. Nonlinear Sci., 2003, 13, 209–264. doi: 10.1007/s00332-002-0531-z [38] M. J. Ward and J. Wei, Hopf bifurcation of spike solutions for the shadow Gierer–Meinhardt model, Eur. J. Appl. Math., 2003, 14(6), 677–711. doi: 10.1017/S0956792503005278 -
-
-
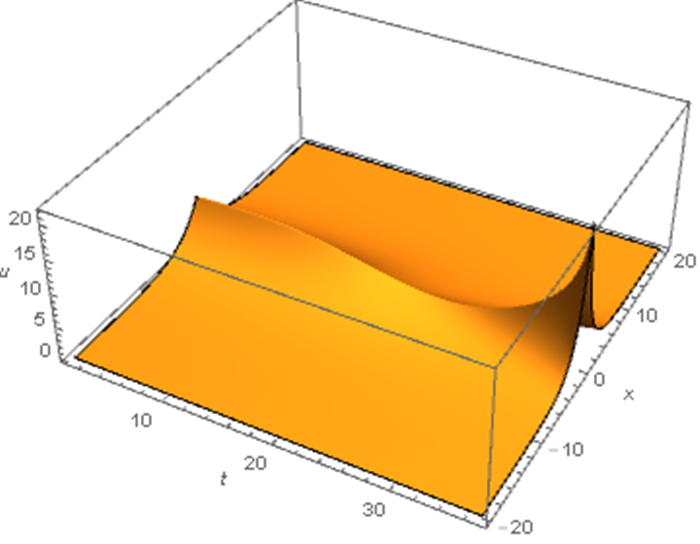
Figure 1.
$ b_r>0 $ $ \mu<\hat{\mu}. $ -
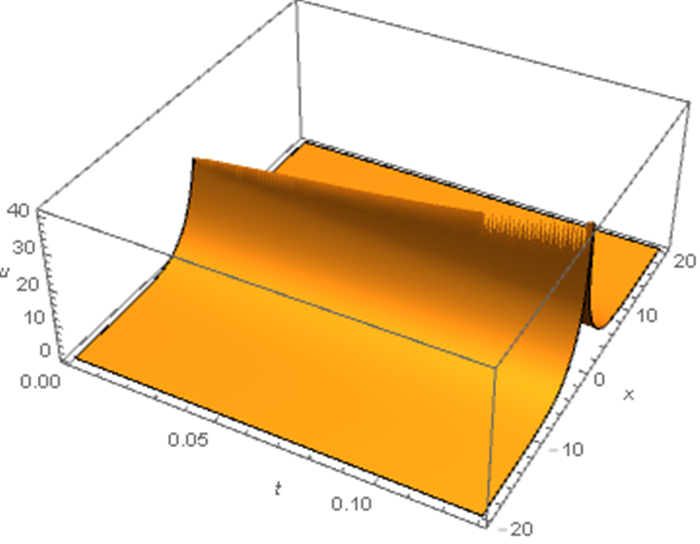
Figure 2.
$ b_r>0 $ $ \mu<\hat{\mu}. $ -
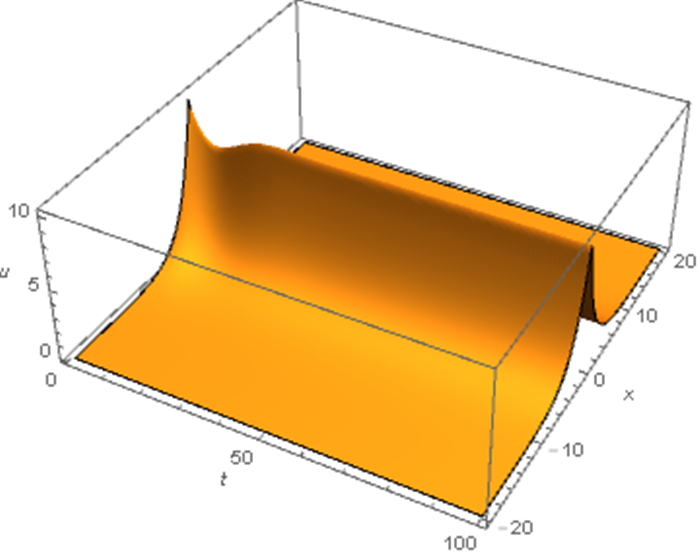
Figure 3.
$ b_r>0 $ $ \mu>\hat{\mu} $ -
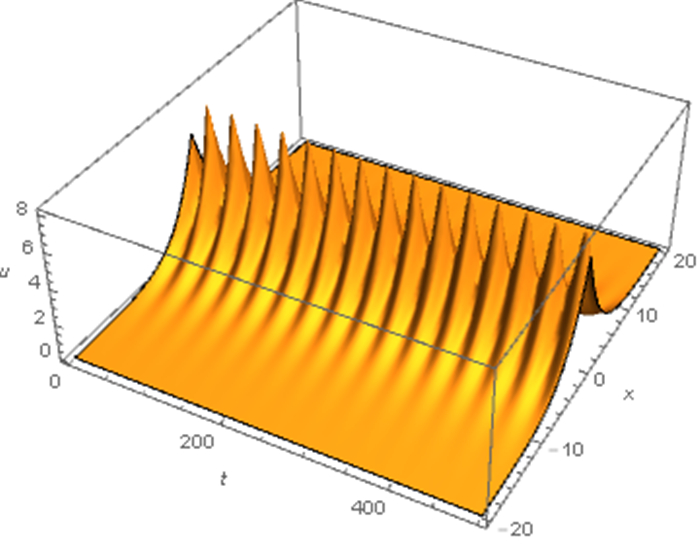
Figure 4.
$ b_r<0 $ $ \mu>\hat{\mu}. $




 DownLoad:
DownLoad: