| Citation: | Hadjer Zerouali, Ahcene Merad, Ali Akgül, Douha Saadi, Nourhane Attia, Evren Hincal. NUMERICAL METHOD FOR SOLVING PSEUDO-HYPERBOLIC EQUATIONS WITH PURELY INTEGRAL CONDITIONS IN REPRODUCING KERNEL HILBERT SPACE[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 2611-2636. doi: 10.11948/20240340 |
NUMERICAL METHOD FOR SOLVING PSEUDO-HYPERBOLIC EQUATIONS WITH PURELY INTEGRAL CONDITIONS IN REPRODUCING KERNEL HILBERT SPACE
-
Abstract
This paper studies a pseudo-hyperbolic equation with purely integral conditions using the reproducing kernel Hilbert space method (RKHSM). By leveraging the properties of reproducing kernel functions (RKFs), we derive exact and approximate solutions to the equation. We present three numerical examples to assess our approach's efficiency and accuracy. The results demonstrate that the RKHSM yields highly accurate approximations, underscoring its effectiveness as a reliable method for solving pseudo-hyperbolic equations with integral constraints. Our findings contribute to the growing research on analytical and numerical techniques for solving such equations.
-

-
References
[1] A. Akgül, A novel method for a fractional derivative with non-local and non-singular kernel, Chaos Solitons Fractals, 2018, 114, 478–482. [2] A. Akgül and E. Bonyah, Reproducing kernel Hilbert space method for the solutions of generalized Kuramoto-Sivashinsky equation, J. Taibah Univ. Sci., 2019, 13(1), 661–669. doi: 10.1080/16583655.2019.1618547 [3] A. Akgül, A. Cordero and J. R. Torregrosa, Solutions of fractional gas dynamics equation by a new technique, Math. Methods Appl. Sci., 2020, 43, 1349–1358. doi: 10.1002/mma.5950 [4] A. Akgül, M. Inc, E. Karatas and D. Baleanu, Numerical solutions of fractional differential equations of Lane-Emden type by an accurate technique, Adv. Differ. Equ., 2015, 2015, 220. doi: 10.1186/s13662-015-0558-8 [5] K. K. Ali, M. A. Abd El Salam, E. M. H. Mohamed, B. Samet, S. Kumar and M. S. Osman, Numerical solution for generalized nonlinear fractional integro-differential equations with linear functional arguments using Chebyshev series, Adv. Differ. Equ., 2020, 2020(1), 494. doi: 10.1186/s13662-020-02951-z [6] T. Allahviranloo and H. Sahihi, Reproducing kernel method to solve fractional delay differential equations, App. Math. Comput., 2021, 400, 126095. doi: 10.1016/j.amc.2021.126095 [7] R. Arima and Y. Hasegawa, On global solutions for mixed problems of a semi-linear differential equation, Proc. Japan Acad., 1963, 39(10), 721–725. [8] N. Aronszajn, Theory of reproducing kernels, Trans. Am. Math. Soc., 1950, 68, 337–404. [9] O. Abu Arqub, M. S. Osman, C. Park, J. R. Lee, H. Alsulami and M. Alhodaly, Development of the reproducing kernel Hilbert space algorithm for numerical pointwise solution of the time-fractional nonlocal reaction-diffusion equation, Alex. Eng. J., 2022, 61(12), 10539–10550. doi: 10.1016/j.aej.2022.04.008 [10] O. Abu Arqub, J. Singh, B. Maayah and M. Alhodaly, Reproducing kernel approach for numerical solutions of fuzzy fractional initial value problems under the Mittag-Leffler kernel differential operator, Math. Methods Appl. Sci., 2023, 46(7), 7965–7986. doi: 10.1002/mma.7305 [11] O. Abu Arqub, S. Tayebi, D. Baleanu, M. S. Osman, W. Mahmoud and H. Alsulami, A numerical combined algorithm in cubic B-spline method and finite difference technique for the time-fractional nonlinear diffusion wave equation with reaction and damping terms, Results Phys., 2022, 41, 105912. [12] A. Attia, A. Akgül, D. Seba and A. Nour, On solutions of time-fractional advection-diffusion equation, Numer. Methods Partial Differ. Equ., 2023, 39(6), 4489–4516. doi: 10.1002/num.22621 [13] B. Azarnavid, The Bernoulli polynomials reproducing kernel method for nonlinear Volterra integro-differential equations of fractional order with convergence analysis, Comput. Appl. Math., 2022, 42(1), 8. [14] E. Babolian, S. Javadi and E. Moradi, RKM for solving Bratu-type differential equations of fractional order, Math. Meth. Appl. Sci., 2016, 39(6), 1548–1557. doi: 10.1002/mma.3588 [15] S. Bergman, Sur un lien entre la théorie des equations aux derivées partielles elliptiques et celle des functions d'une variable complexe, C. R. Acad. Sci. Paris, 1937, 205, 1198. [16] H. Beyrami and T. Lotfi, A novel method with error analysis for the numerical solution of a logarithmic singular Fredholm integral equation, Afr. Mat., 2023, 34(2), 33. doi: 10.1007/s13370-023-01073-5 [17] A. Bouziani, On a classe of nonclassical hyperbolic equations with nonlocal conditions, Int. J. Stoch. Anal., 2002, 15(2), 141476. [18] A. Bouziani and N.-E. Benouar, Mixed problem with integral conditions for a third order parabolic equation, Kobe J. Math., 1998, 15(1), 47–58. [19] Y. Chellouf, B. Maayah, S. Momani, A. Alawneh and S. Alnabulsi, Numerical solution of fractional differential equations with temporal two-point BVPs using reproducing kernal Hilbert space method, AIMS Math, 2021, 6(4), 3465–3485. doi: 10.3934/math.2021207 [20] M. Cui and Y. Lin, Nonlinear Numerical Analysis in Reproducing Kernel Space, Nova Science Publishers, Inc., 2009. [21] K. Dehingia, S. Boulaaras, E. Hinçal, K. Hosseini, T. Abdeljawad and M. S. Osman, On the dynamics of a financial system with the effect financial information, Alex. Eng. J., 2024, 106, 438–447. doi: 10.1016/j.aej.2024.08.049 [22] S. Djennadi, N. Shawagfeh, M. Inc, M. S. Osman, J. F. Gómez-Aguilar and O. Abu Arqub, The Tikhonov regularization method for the inverse source problem of time fractional heat equation in the view of ABC-fractional technique, Phys. Scr., 2021, 96(9), 094006. doi: 10.1088/1402-4896/ac0867 [23] M. Fardi and M. Ghasemi, Solving nonlocal initial-boundary value problems for parabolic and hyperbolic integro-differential equations in reproducing kernel hilbert space, Numer. Methods Partial Differ. Equ., 2017, 33(1), 174–198. doi: 10.1002/num.22079 [24] F. Geng and M. Cui, New method based on the HPM and RKHSM for solving forced Duffing equations with integral boundary conditions, J. Comput. Appl. Math., 2009, 233(2), 165–172. doi: 10.1016/j.cam.2009.07.007 [25] H. Guo and H. Rui, Least-squares Galerkin procedures for pseudohyperbolic equations, Appl. Math. Comput., 2007, 189(1), 425–439. [26] F. Hemati, M. Ghasemi and R. Khoshsiar Ghaziani, Numerical solution of the multiterm time-fractional diffusion equation based on reproducing kernel theory, Numer. Methods Partial Differ. Equ., 2021, 37(1), 44–68. doi: 10.1002/num.22518 [27] M. Inc and A. Akgül, The reproducing kernel Hilbert space method for solving Troesch's problem, J. Assoc. Arab Univ. Basic Appl. Sci., 2013, 14(1), 19–27. [28] W. Jiang and M. Cui, Solving nonlinear singular pseudoparabolic equations with nonlocal mixed conditions in the reproducing kernel space, Int. J. Comput. Math., 2010, 87(15), 3430–3442. [29] A. Khalid, A. S. A. Alsubaie, M. Inc, A. Rehan, W. Mahmoud and M. S. Osman, Cubic splines solutions of the higher order boundary value problems arise in sandwich panel theory, Results Phys., 2022, 39, 105726. [30] S. Kumar, R. P. Chauhan, M. S. Osman and S. A. Mohiuddine, A study on fractional HIV-AIDs transmission model with awareness effect, Math. Methods Appl. Sci., 2023, 46(7), 8334–8348. [31] X. Li and B. Wu, New algorithm for nonclassical parabolic problems based on the reproducing kernel method, Math. Sci., 2013, 7(1), 4. [32] Y. Lin and Y. Zhou, Solving nonlinear pseudoparabolic equations with nonlocal boundary conditions in reproducing kernel space, Numer. Algorithms, 2009, 52(2), 173–186. [33] Y. Liu, H. Li, J. Wang and S. He, Splitting positive definite mixed element methods for pseudo-hyperbolic equations, Numer. Methods Partial Differ. Equ., 2012, 28(2), 670–688. [34] Y. Liu, J. Wang, H. Li, W. Gao and S. He, A new splitting $H. 1$-Galerkin mixed method for pseudo-hyperbolic equations, Int. J. Comput. Math., 2011, 5(3), 413–418. [35] V. A. Makhlai, I. E. Garkusha, S. S. Herashchenko, O. V. Byrka, N. N. Aksenov, S. V. Malykhin, S. V. Surovitskiy and M. Wirtz, Contribution of leading edge shape to a damaging of castellated tungsten targets exposed to repetitive QSPA plasma loads, Phys. Scr., 2021, 96(12), 124043. doi: 10.1088/1402-4896/ac2d86 [36] A. Merad and A. Bouziani, Laplace transform technique for pseudoparabolic equation with nonlocal conditions, TJMM, 2013, 5(1), 59–64. [37] A. Merad and A. Bouziani, Solvability the telegraph equation with purely integral conditions, TWMS J. App. Eng. Math., 2013, 3(1), 117–125. [38] A. Merad, A. Bouziani and S. Araci, Existence and uniqueness for a solution of pseudohyperbolic equation with nonlocal boundary condition, Appl. Math. Inf. Sci., 2015, 9(4), 1855–1861. [39] S. Momani, N. Djeddi, M. Al-Smadi and S. Al-Omari, Numerical investigation for Caputo-Fabrizio fractional Riccati and Bernoulli equations using iterative reproducing kernel method, Appl. Numer. Math., 2021, 170, 418–434. [40] J. Nagumo, S. Arimoto and S. Yoshizawa, An active pulse transmission line simulating nerve axon, Proc. IRE., 1962, 50(10), 2061–2070. [41] A. Necib and A. Merad, Laplace transform and homotopy perturbation methods for solving the pseudohyperbolic integrodifferential problems with purely integral conditions, KJM, 2020, 44(2), 251–272. [42] C. V. Pao, A mixed initial boundary-value problem arising in neurophysiology, J. Math. Anal. Appl., 1975, 52(1), 105–119. [43] G. Ponce, Global existence of small solutions to a class of nonlinear evolution equations, Nonlinear Anal. Theory Methods Appl., 1985, 9(5), 399–418. [44] L. S. Pulkina, Solution to nonlocal problems of pseudohyperbolic equations, EJDE, 2012, 2012(116), 1–9. [45] S. Rashid, K. T. Kubra, S. Sultana, P. Agarwal and M. S. Osman, An approximate analytical view of physical and biological models in the setting of Caputo operator via Elzaki transform decomposition method, J. Comput. Appl. Math., 2022, 413, 114378. [46] M. G. Sakar, O. Saldır and A. Akgül, A novel technique for fractional Bagley-Torvik equation, Proc. Natl. Acad. Sci. India Sect. A Phys. Sci., 2019, 89(3), 539–545. [47] L. Shi, S. Tayebi, O. Abu Arqub, M. S. Osman, P. Agarwal, W. Mahamoud, M. Abdel-Aty and M. Alhodaly, The novel cubic B-spline method for fractional Painlevé and Bagley-Trovik equations in the Caputo, Caputo-Fabrizio, and conformable fractional sense, Alex. Eng. J., 2023, 65, 413–426. [48] L.-H. Yang and Y. Lin, Reproducing kernel methods for solving linear initial-Boundary-value problems, EJDE, 2008, 2008(29), 1–11. [49] S. Zaremba, Sur le calcul numérique des fonctions demandées dans le probléme de Dirichlet et le probléme hydrodynamique, Bull. Int. Acad. Sci. Crac., 1908, 68, 125–195. -
-
-
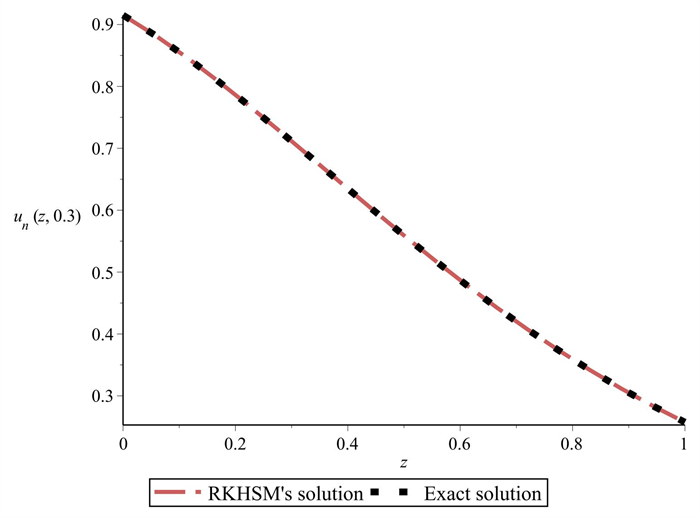
Figure 1.
RKHSM and Exact solutions for Example 5.1 when
$ l=0.3. $ -
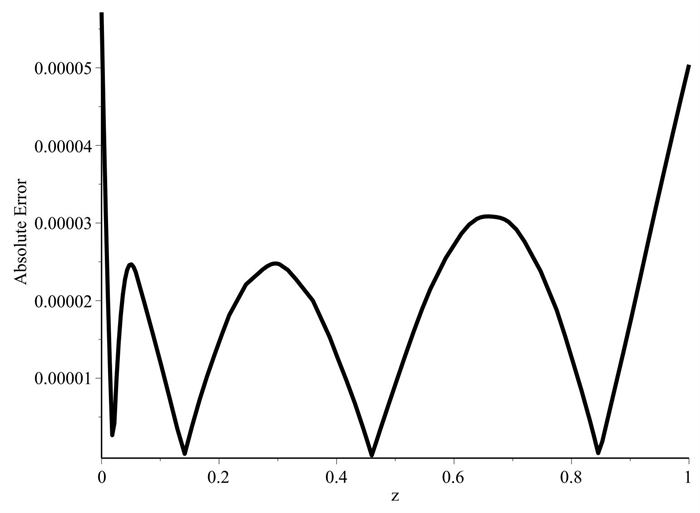
Figure 2.
Absolute error of the RKHSM for Example 5.1 when
$ l=0.3. $ -
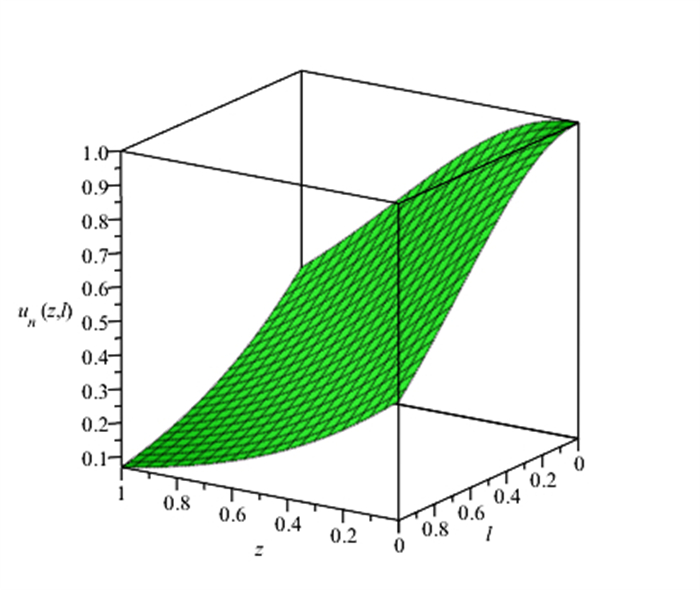
Figure 3.
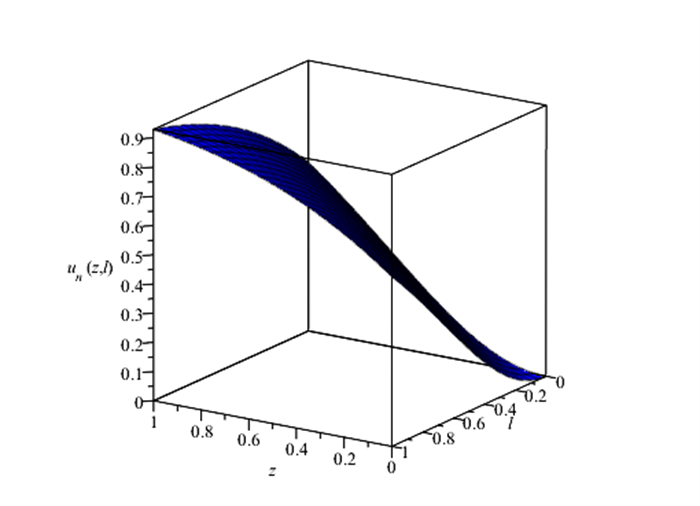
3D Visualization of the RKHSM's solution for Example 5.1.
-
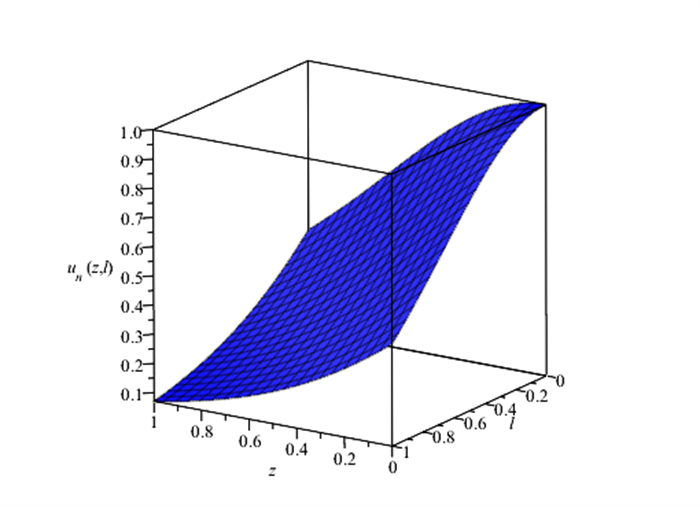
Figure 4.
3D Visualization of the exact solution solution for Example 5.1.
-
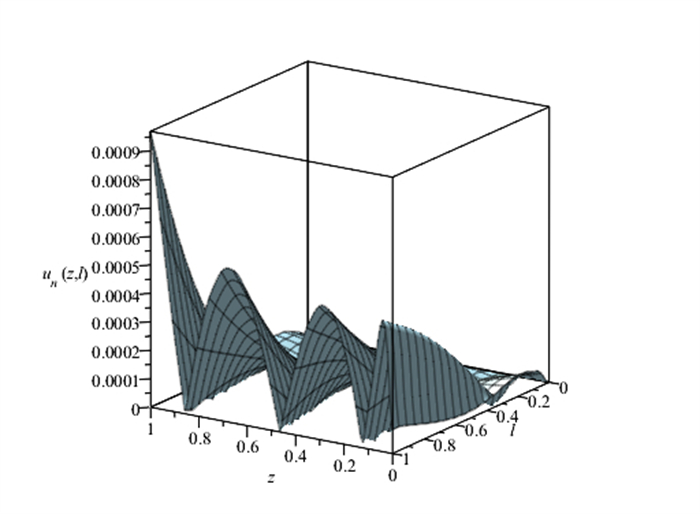
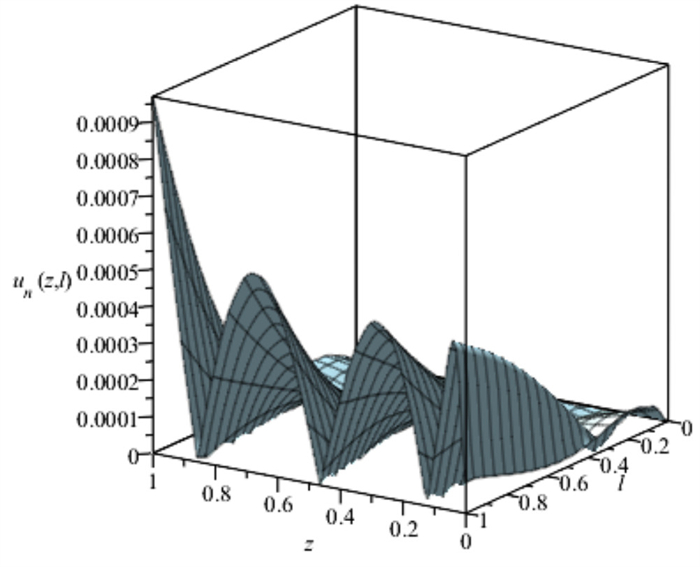
Figure 5.
3D Visualization of the absolute error for Example 5.1.
-
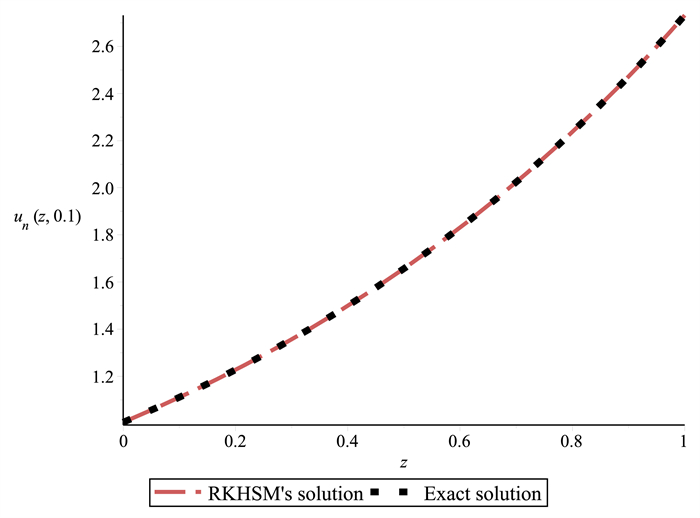
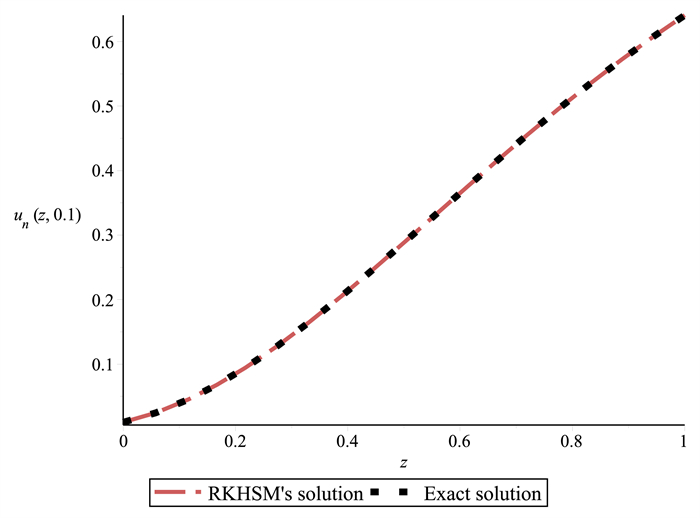
Figure 6.
RKHSM and Exact solutions for Example 5.2 when
$ l=0.1. $ -
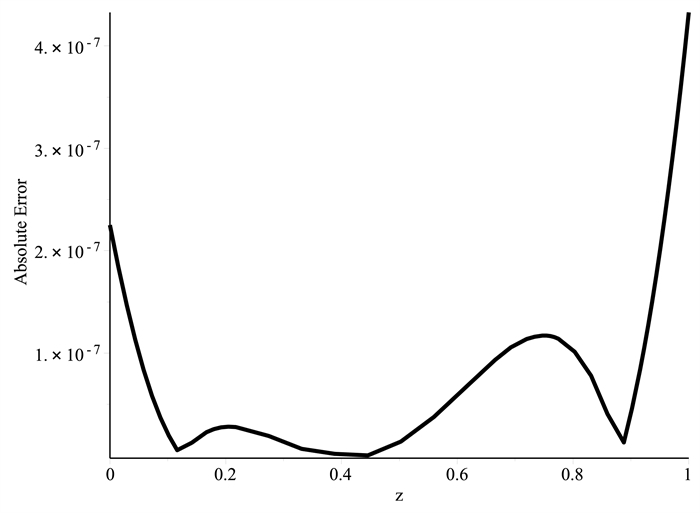
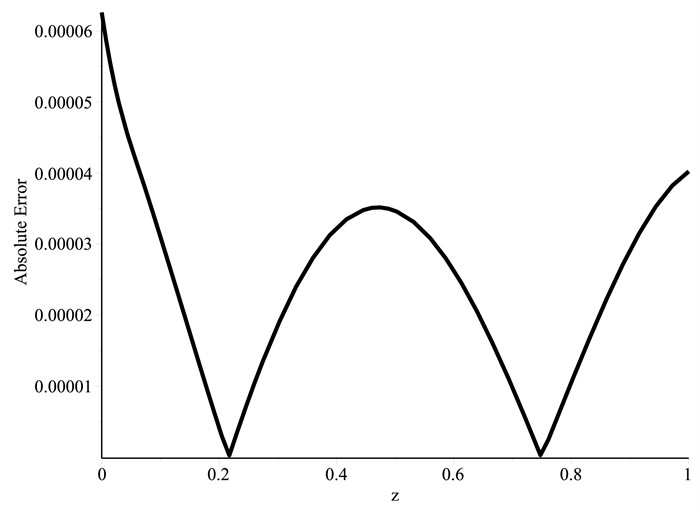
Figure 7.
Absolute error of the RKHSM for Example 5.2 when
$ l=0.1. $ -
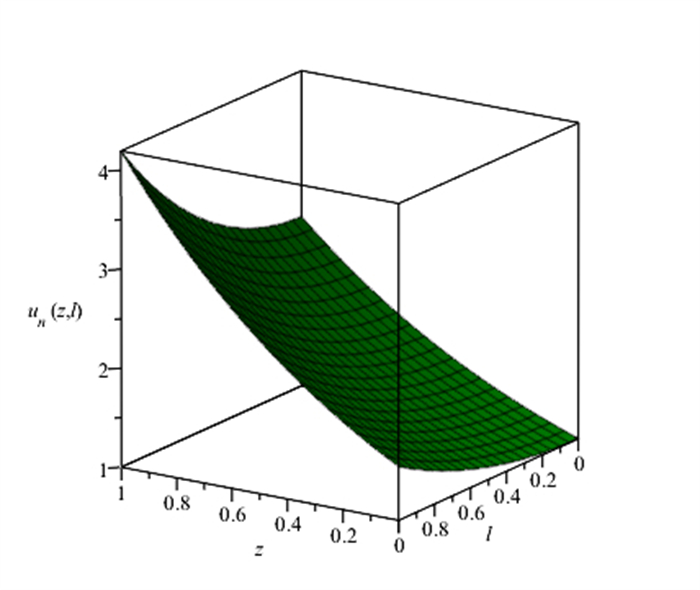
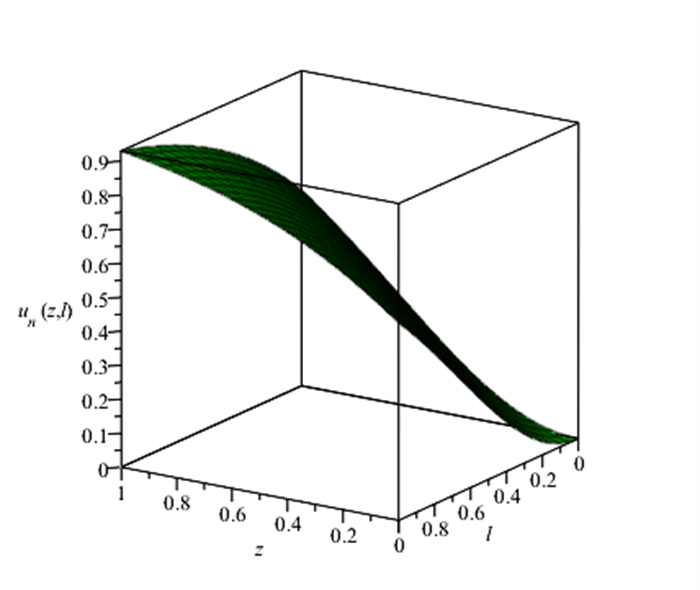
Figure 8.
3D Visualization of the RKHSM's solution for Example 5.2.
-
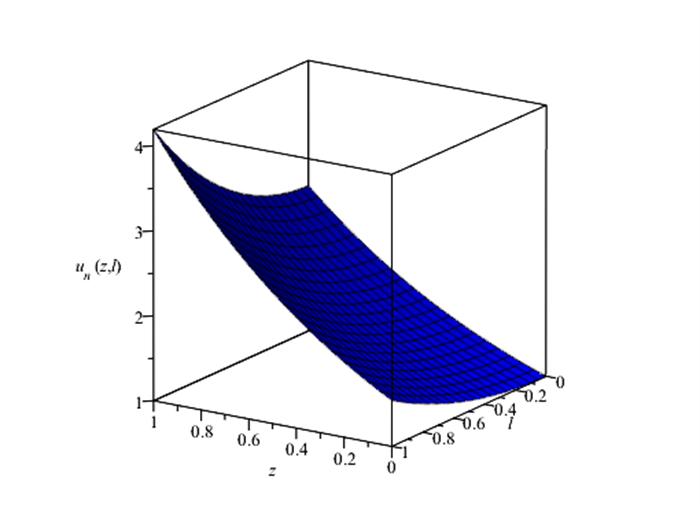
Figure 9.
3D Visualization of the exact solution solution for Example 5.2.
-
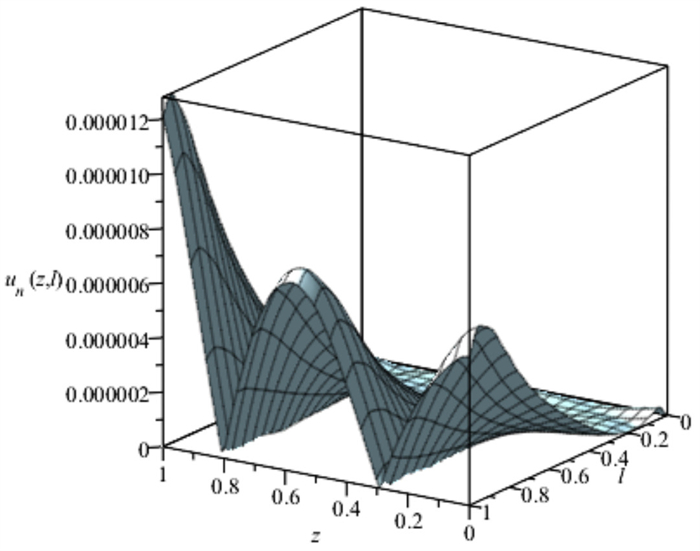
Figure 10.
3D Visualization of the absolute error for Example 5.2.
-
Figure 11.
RKHSM and Exact solutions for Example 5.3 when
$ l=0.1. $ -
Figure 12.
Absolute error of the RKHSM for Example 5.3 when
$ l=0.1. $ -
Figure 13.
3D Visualization of the RKHSM's solution for Example 5.3.
-
Figure 14.
3D Visualization of the exact solution solution for Example 5.3.
-
Figure 15.
3D Visualization of the absolute error for Example 5.3.




 DownLoad:
DownLoad: