| Citation: | Jinsen Zhuang, Yan Zhou, Jibin Li. BIFURCATIONS AND EXACT SOLUTIONS OF THE DERIVATIVE NONLINEAR SCHRÖDINGER EQUATIONS DNLSI-DNLSIII: DYNAMICAL SYSTEM METHOD[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 2637-2651. doi: 10.11948/20240390 |
BIFURCATIONS AND EXACT SOLUTIONS OF THE DERIVATIVE NONLINEAR SCHRÖDINGER EQUATIONS DNLSI-DNLSIII: DYNAMICAL SYSTEM METHOD
-
Abstract
For the derivative nonlinear Schrödinger equations DNLSI-DNLSIII, by using the dynamical system method, we investigate the exact explicit solutions with the form $ q(x, t)=\phi(\xi)\exp{[i(\kappa x-\omega t+\theta(\xi))]}, \xi=x-ct. $ In the given parameter regions, we present exact explicit parametric representations for more than 14 solutions.
-

-
References
[1] K. Abhinav, P. Guha and I. Mukherjee, Study of quasi-integrable and non-holonomic deformation of equations in the NLS and DNLS hierarchy, J. Math. Phys., 2018, 59, 101507. doi: 10.1063/1.5019268 [2] T. Aydemir, New exact optical soliton solutions of the derivative nonlinear Schrödinger equation family, Opt. Quant. Electron., 2024, 56(6). DOI: 10.1007/s11082-024-06822-9. [3] H. M. Baskonus, M. Younis, M. Bilal, U. Younas, Shafqat-ur-Rehman and W. Gao, Modulation instability analysis and perturbed optical soliton and other solutions to the Gerdjikov-Ivanov equation in nonlinear optics, Modern Phys. Lett., 2020, 34(35), 2050404. doi: 10.1142/S0217984920504047 [4] P. F. Byrd and M. D. Fridman, Handbook of Elliptic Integrals for Engineers and Sciensists, Springer, Berlin, 1971. [5] H. H. Chen, Y. C. Lee and C. S. Liu, Integrability of nonlinear Hamiltonian systems by inverse scattering method, Phys. Scr., 1979, 20, 490. doi: 10.1088/0031-8949/20/3-4/026 [6] M. Chen, Bifurcations and exact solutions for the Kundu equation: Dynamical approach, J. Appl. Anal. Comput., 2024, 14(6). DOI: 10.11948/JAAC-2024-0012. [7] H. H. Dai and E. G. Fan, Variable separation and algebro-geometric solutions of the Gerdjikov–Ivanov equation, Chaos Soliton. Fract., 2004, 22, 93–101. [8] M. Dong, L. Tian, J. Wei and Y. Wang, Some localized wave solutions for the coupled Gerdjikov-Ivanov equation, Appl. Math. Lett., 2021, 122, 107483. doi: 10.1016/j.aml.2021.107483 [9] E. G. Fan, Integrable systems of derivative nonlinear Schrödinger type and their multi-Hamiltonian structure, J. Phys. A Math. Gen., 2001, 34, 513–519. doi: 10.1088/0305-4470/34/3/313 [10] E. G. Fan, Bi-Hamiltonian structure and Liouville integrablity for a Gerdjikov–Ivanov equation hierarchy, Chin. Phys. Lett., 2001, 18, 1–3. doi: 10.1088/0256-307X/18/1/301 [11] N. G. Fang, Darboux transformation and soliton-like solutions for the Gerdjikov–Ivanov equation, J. Phys. A: Math. Gen., 2000, 33, 6925–6933. doi: 10.1088/0305-4470/33/39/308 [12] S. Fromm, Admissible boundary values for the Gerdjikov-Ivanov equation with asymptotically time-periodic boundary data, SIGMA Symmetry Integrability Geom. Methods Appl., 2020, 16, 79. [13] V. S. Gerdjikov and M. I. Ivanov, A quadratic pencil of general type and nonlinear evolution equations. Ⅱ. Hierarchies of Hamiltonian structures, Bulg. J. Phys., 1983, 10(1), 13. [14] S. C. A. Gómez, A. Jhangeer, H. Rezazadeh, R. A. Talarposhti and A. Bekir, Closed form solutions of the perturbed Gerdjikov-Ivanov equation with variable coefficients, East Asian J. Appl. Math., 2021, 11(1), 207–218. doi: 10.4208/eajam.230620.070920 [15] H. Indexed, M. Saleh and A. A. Altwaty, Optical solitons of the extended Gerdjikov-Ivanov equation in DWDM system by extended simplest equation method, Appl. Math. Inf. Sci., 2020, 14(5), 901–907. doi: 10.18576/amis/140517 [16] A. Kalbani, K. Kaltham, K. S. Al-Ghafri, E. V. Krishnan and A. Biswas, Solitons and modulation instability of the perturbed Gerdjikov-Ivanov equation with spatio-temporal dispersion, Chaos Soliton. Fract., 2021, 153, 111523. doi: 10.1016/j.chaos.2021.111523 [17] D. J. Kaup and A. C. Newell, An exact solution for a derivative nonlinear Schrödinger equation, J. Math. Phys., 1978, 19(4), 798. [18] M. M. A. Khater, Abundant wave solutions of the perturbed Gerdjikov-Ivanov equation in telecommunication industry, Modern Phys. Lett., 2021, 35(26), 2150456. doi: 10.1142/S021798492150456X [19] S. A. Khuri, New optical solitons and traveling wave solutions for the Gerdjikov-Ivanov equation, Optik, 2022, 268(39), 169784. [20] J. Li, Singular Nonlinear Traveling Wave Equations: Bifurcations and Exact Solutions, Science Press, Beijing, 2013. [21] M. Li, Y. Zhang, R. Ye and Y. Lou, Exact solutions of the nonlocal Gerdjikov-Ivanov equation, Commun. Theor. Phys., 2021, 73, 10. [22] Y. Li, L. Zhang, B. Hu and R. Wang, The initial-boundary value for the combined Schrödinger and Gerdjikov–Ivanov equation on the half-line via the Riemann–Hilbert approach, Teoret. Mat. Fiz., 2021, 209(2), 258–273. doi: 10.4213/tmf10141 [23] Y. Lou, Y. Zhang, R. Ye and M. Li, Modulation instability, higher-order rogue waves and dynamics of the Gerdjikov-Ivanov equation, Wave Motion, 2021, 106, 102795. [24] P. Lu, Y. Wang and C. Dai, Abundant fractional soliton solutions of a space-time fractional perturbed Gerdjikov-Ivanov equation by a fractional mapping method, Chinese J. Phys., 2021, 74, 96–105. [25] J. Luo and E. Fan, Dbar-dressing method for the Gerdjikov-Ivanov equation with nonzero boundary conditions, Appl. Math. Lett., 2021, 120, 107297. [26] J. Luo and E. Fan, $\varrho$-dressing method for the coupled Gerdjikov-Ivanov equation, Appl. Math. Lett., 2020, 110, 106589. $\varrho$-dressing method for the coupled Gerdjikov-Ivanov equation" target="_blank">Google Scholar
[27] S. T. R. Rizvi and S. Shabbir, Optical soliton solution via complete discrimination system approach along with bifurcation and sensitivity analyses for the Gerjikov-Ivanov equation, Optik, 2023, 294(5), 171456. [28] T. Tsuchida, Integrable discretizations of derivative nonlinear Schrödinger equations, J. Phys. A Math. Gen. 2002, 35, 7827–7847. [29] Vinita and S. Saha Ray, Lie symmetry reductions, power series solutions and conservation laws of the coupled Gerdjikov-Ivanov equation using optimal system of Lie subalgebra, Z. Angew. Math. Phys., 2021, 72(4), 133. [30] X. Xiao and Z. Yin, Exact single travelling wave solutions to the fractional perturbed Gerdjikov-Ivanov equation in nonlinear optics, Modern Phys. Lett. 2021, 35, 22. [31] S. Zhang, T. Xu, M. Li and X. Zhang, Higher-order algebraic soliton solutions of the Gerdjikov-Ivanov equation: Asymptotic analysis and emergence of rogue waves, Phys. D, 2022, 432, 133128. [32] Z. Zhang and E. Fan, Inverse scattering transform and multiple high-order pole solutions for the Gerdjikov-Ivanov equation under the zero/nonzero background, Z. Angew. Math. Phys., 2021, 72(4), 153. [33] Z. Zhang and E. Fan, Inverse scattering transform for the Gerdjikov-Ivanov equation with nonzero boundary conditions, Z. Angew. Math. Phys., 2020, 71(5), 149. [34] Y. Zhou and J. Li, Bifurcations of traveling wave solutions in the homogeneous Camassa-Holm type equations, J. Appl. Anal. Comput., 2022, 12(1), 392–406. [35] J. Zhu and Y. Chen, A new form of general soliton solutions and multiple zeros solutions for a higher-order Kaup-Newell equation, J. Math. Phys., 2021, 62, 12. [36] J. Zhuang and Y. Zhou, Bifurcations of solitary waves, periodic peakons and compactons of a coupled nonlinear wave equation, J. Appl. Anal. Comput., 2022, 12(5), 1–7. -
-
-
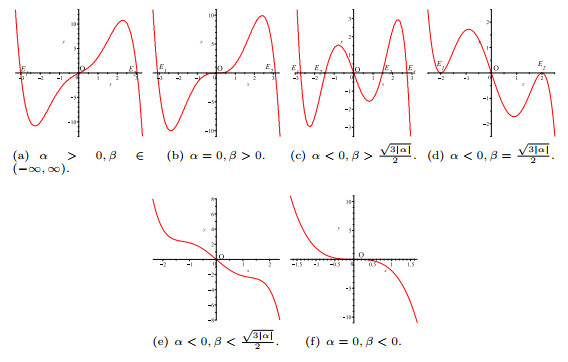
Figure 1.
The real roots of
$ f(\phi)=0. $ -
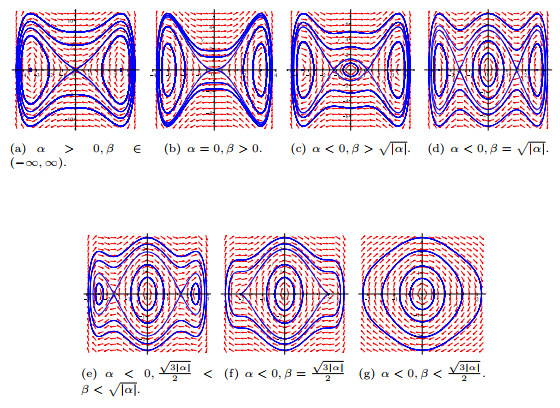
Figure 2.
The bifurcations of phase portraits of system (2.15).




 DownLoad:
DownLoad: