| Citation: |
Ahmed Bchatnia, Abderrahmane Beniani, Boumediene Boukhari, Foued Mtiri. THEORETICAL AND NUMERICAL STABILITY OF THE BRESSE SYSTEM: EXPLORING FRACTIONAL DAMPING THROUGH TRADITIONAL AND NEURAL NETWORK APPROACHES[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 2663-2694. doi: 10.11948/20240410
|
THEORETICAL AND NUMERICAL STABILITY OF THE BRESSE SYSTEM: EXPLORING FRACTIONAL DAMPING THROUGH TRADITIONAL AND NEURAL NETWORK APPROACHES
-
Abstract
This paper investigates the theoretical and numerical stability of the one-dimensional Bresse system with fractional damping terms in a bounded domain. We first establish the well-posedness of the system. Using the frequency domain approach and a theorem by Borichev and Tomilov, we derive the polynomial decay rate of the system. To validate these theoretical results, we propose a numerical scheme and compare its performance with the Fractional Physics-Informed Neural Network (fPINN). The comparative analysis highlights the effectiveness of traditional numerical methods and fPINNs in capturing the decay rate, offering new insights into the advancement of computational techniques for complex physical systems.
-
-
References
[1] Z. Achouri, N. Amroun and A. Benaissa, The Euler Bernoulli beam equation with boundary dissipation of fractional derivative, Math. Methods Appl. Sci., 2017, 40(11), 3837–3854. doi: 10.1002/mma.4267 [2] M. Akil, Y. Chitour, M. Ghader and A. Wehbe, Stability and exact controllability of a Timoshenko system with only one fractional damping on the boundary, Asymptotic Analysis, 2020, 119(3), 221–280. DOI: 10.3233/ASY-191574. [3] M. Akil, M. Ghader and A. Wehbe, The influence of the coefficients of a system of wave equations coupled by velocities with fractional damping on its boundary stabilization, Bull. Span. Soc. Appl. Math. SEMA, 2021, 78, 287–333. DOI: 10.1007/s40324-020-00233-y. [4] M. Akil, I. Issa and A. Wehbe, Energy decay rate of the Euler-Bernoulli beam and wave equations via boundary connection with one locally non-regular fractional Kelvin-Voigt damping, Math. Control Relat. Fields, 2023, 13(1), 330–381. doi: 10.3934/mcrf.2021059 [5] M. Akil and A. Wehbe, Indirect stability of a multidimensional coupled wave equations with one locally boundary fractional damping, Math. Nachr., 2022, 295(12), 2272–2300. DOI: 10.1002/mana.202100185. [6] M. Akil and A. Wehbe, Stabilization of multidimensional wave equation with locally boundary fractional dissipation law under geometric conditions, Math. Control Relat. Fields, 2019, 9(1), 97–116. doi: 10.3934/mcrf.2019005 [7] S. Alfalqi, B. Boukhari, A. Bchatnia and A. Beniani, Advanced neural network approaches for coupled equations with fractional derivatives, Bound. Value Probl., 2024, 96, 1–18. [8] D. S. Almeida Junior, J. E. Munoz Rivera and M. L. Santos, Bresse system with Fourier law on shear force, Adv. Differ. Equ., 2016, 21(1–2), 55–84. [9] M. O. Alves, L. H. Fatori, M. A. Jorge Silva and R. N. Monteiro, Stability and optimality of decay rate for a weakly dissipative Bresse system, Math. Methods Appl. Sci., 2015, 38, 898–908. doi: 10.1002/mma.3115 [10] T. El Arwadi, M. I. M. Copetti and W. Youssef, On the theoretical and numerical stability of the thermoviscoelastic Bresse system, Z. Angew. Math. Mech., 2019, 99. [11] C. J. K. Batty, R. Chill and Y. Tomilov, Fine scales of decay of operator semigroups, J. Eur. Math. Soc. (JEMS), 2016, 18, 853–929. doi: 10.4171/jems/605 [12] A. Beniani, N. Bahri, R. Alharbi, K. Bouhali and Kh. Zennir, Stability for weakly coupled wave equations with a general internal control of diffusive type, Axioms, 2023, 12(1), 48. DOI: 10.3390/axioms12010048. [13] C. Bernardi and M. I. M. Copetti, Discretization of a nonlinear dynamic thermoviscoelastic Timoshenko beam model, Z. Angew. Math. Mech., 2017, 97, 532–549. doi: 10.1002/zamm.201500193 [14] J. A. C. Bresse, Cours de Mécaniques Appliquée, Mallet-Bachelier, Paris, 1859. [15] M. Bzeih, T. El Arwadi and M. Hindi, Numerical analysis and simulation for Rayleigh beam equation with dynamical boundary controls, Arab. J. Math., 2021, 10, 331–349. doi: 10.1007/s40065-021-00310-8 [16] M. I. M. Copetti, T. El Arwadi, J. R. Fernández, M. G. Naso and W. Youssef, Analysis of a contact problem for a viscoelastic Bresse system, ESAIM Math. Model. Numer. Anal., 2021, 55, 887–911. doi: 10.1051/m2an/2021015 [17] L. H. Fatori and J. E. Muñoz Rivera, Rates of decay to weak thermoelastic Bresse system, IMA J. Appl. Math., 2010, 75, 881–904. doi: 10.1093/imamat/hxq038 [18] Z. Liu and B. Rao, Energy decay rate of the thermoelastic Bresse system, Z. Angew. Math. Phys., 2009, 60, 54–69. doi: 10.1007/s00033-008-6122-6 [19] B. Mbodje, Wave energy decay under fractional derivative controls, IAM J. Control Optim, 2006, 23, 237–257. [20] M. A. Rincon and M. I. M. Copetti, Numerical analysis for a locally damped wave equation, J. Appl. Anal. Comput., 2013, 30, 169–182. [21] M. L. Santos and D. S. Almeida Junior, Numerical exponential decay to dissipative Bresse system, J. Appl. Math., 2010. -
-
Figures(8) / Tables(2)
Export File
Citation
Ahmed Bchatnia, Abderrahmane Beniani, Boumediene Boukhari, Foued Mtiri. THEORETICAL AND NUMERICAL STABILITY OF THE BRESSE SYSTEM: EXPLORING FRACTIONAL DAMPING THROUGH TRADITIONAL AND NEURAL NETWORK APPROACHES[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 2663-2694. doi: 10.11948/20240410
Format
Content
DownLoad:
-
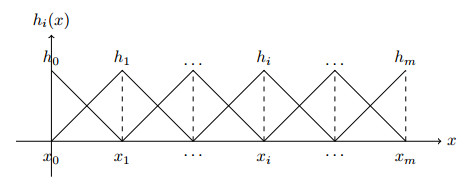
Figure 1.
Piecewise Linear Interpolation Functions
$ h_i(x) $ $ (x_0, x_m) $ -
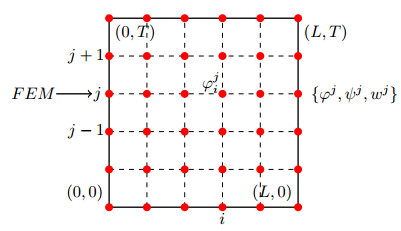
Figure 2.
Mesh of the domain
$ [0, L] \times [0, T] $ $ (x_i, t_j) $ -
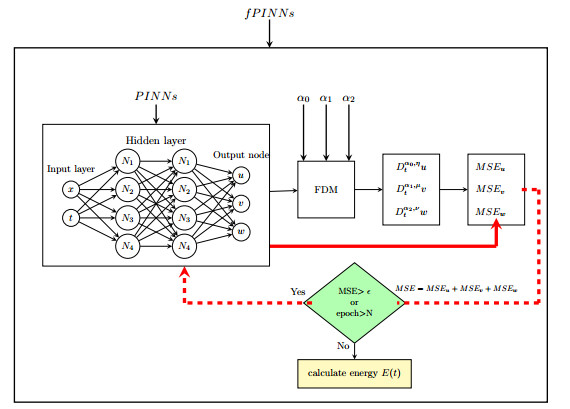
Figure 3.
fPINNs to solve the problem (5) for calculate energy E(t).
-
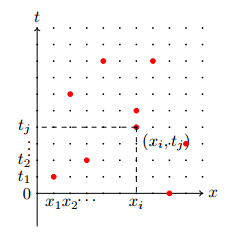
Figure 4.
Point cloud used for training the PINN and calculating the fractional derivative for each point
$ (x_i, t_j) $ -
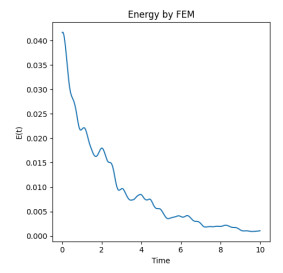
Figure 5.
Energy by FEM for
$ T=10 $ -
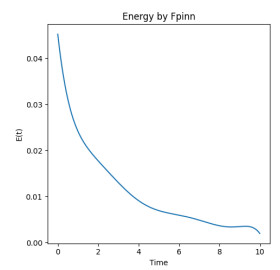
Figure 6.
Energy by fPINN for
$ T=10 $ -
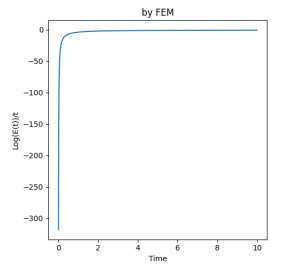
Figure 7.
Log Energy/t by FEM for
$ T=10 $ -
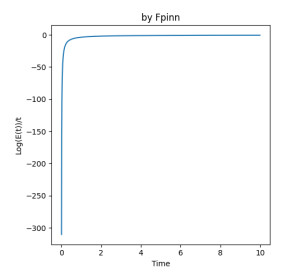
Figure 8.
Log Energy/t by fPINN for
$ T=10 $