| Citation: | Zhilong Shi, Linru Nie, Jibin Li. EXACT SOLUTIONS OF TWO HIGH ORDER DERIVATIVE NONLINEAR SCHRÖDINGER EQUATIONS: DYNAMICAL SYSTEM METHOD[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1820-1829. doi: 10.11948/20240451 |
EXACT SOLUTIONS OF TWO HIGH ORDER DERIVATIVE NONLINEAR SCHRÖDINGER EQUATIONS: DYNAMICAL SYSTEM METHOD
-
Abstract
For two generalization models of the first type derivative nonlinear Schrödinger (DNLSI) equation and the second type derivative nonlinear Schrödinger (DNLSII) equation, by using the method of dynamical systems to investigate the existence of exact explicit solutions with the form $ q(x,t)=\phi(\xi)\exp{[i(\kappa x-\omega t+\theta(\xi))]}, \xi=x-ct. $ This paper show that in some given parameter conditions, explicit exact parametric representations of $ \phi(\xi)$ and $\theta(\xi) $ can be given.
-

-
References
[1] H. M. Baskonus, M. Younis, M. Bilal, et al., Modulation instability analysis and perturbed optical soliton and other solutions to the Gerdjikov-Ivanov equation in nonlinear optics, Modern Phys. Lett. B, 2020, 34(35), 2050404. doi: 10.1142/S0217984920504047 [2] H. H. Chen, Y. C. Lee and C. S. Liu, Integrability of nonlinear Hamiltonian systems by inverse scattering method, Phys. Scr., 1979, 20, 490. doi: 10.1088/0031-8949/20/3-4/026 [3] Q. Cheng, Z. Zhang, Q. Wang, et al., Solitary, periodic, kink wave solutions of a perturbed high-order nonlinear Schrödinger equation via bifurcation theory, Propulsion and Power Research, 2024, 13(3), 433–444. doi: 10.1016/j.jppr.2024.07.001 [4] R. Cheng, Z. Luo and X. Hong, Bifurcations and new traveling wave solutions for the nonlinear dispersion Drinfel'd-Sokolov (D(m, n)) system, Journal of Nonlinear Modeling and Analysis, 2021, 3(2), 193–207. [5] H. Dai and E. Fan, Variable separation and algebro-geometric solutions of the Gerdjikov-Ivanov equation, Chaos Solitons & Fractals, 2004, 22(1), 93–101. [6] M. Dong, L. Tian, J. Wei, et al., Some localized wave solutions for the coupled Gerdjikov-Ivanov equation, Applied Mathematics Letters, 2021, 122, 107483. doi: 10.1016/j.aml.2021.107483 [7] E. Fan, Darboux transformation and soliton-like solutions for the Gerdjikov-Ivanov equation, Journal of Physics. A. Mathematical and General: A Europhysics Journal, 2000, 33(39), 6925–6933. [8] E. Fan, Integrable evolution systems based on Gerdjikov-Ivanov equations, bi-Hamiltonian structure, finite-dimensional integrable systems and N-fold Darboux transformation, J. Math. Phys., 2000, 41(11), 7769–7782. doi: 10.1063/1.1314895 [9] E. Fan, Bi-Hamiltonian structure and Liouville integrablity for a Gerdjikov-Ivanov equation hierarchy, Chin. Phys. Lett., 2001, 18(1), 3. [10] E. Fan, Integrable systems of derivative nonlinear Schrödinger type and their multi-Hamiltonian structure, Journal of Physics A General Physics, 2001, 34(3), 513. [11] E. Fan, A family of completely integrable multi-Hamiltonian systems explicitly related to some celebrated equations, Journal of Mathematical Physics, 2001, 42(9), 4327–4327. doi: 10.1063/1.1389288 [12] Fromm, Samuel admissible boundary values for the Gerdjikov-Ivanov equation with asymptotically time-periodic boundary data, SIGMA Symmetry Integrability Geom. Methods Appl., 2020, 16, 079. [13] V. S. Gerdjikov and M. I. Ivanov, A quadratic pencil of general type and nonlinear evolution equations. Ⅱ. Hierarchies of Hamiltonian structures, Bulg. J. Phys., 1983, 10(1), 13. [14] C. A. S. Gómez, A. Jhangeer, H. Rezazadeh, R. A. Talarposhti and A. Bekir, Closed form solutions of the perturbed Gerdjikov-Ivanov equation with variable coefficients, East Asian J. Appl. Math., 2021, 11(1), 207–218. [15] Q. H. Han and M. Jia, Higher-dimensional Chen-Lee-Liu equation and asymmetric peakon soliton, Chinese Phys. B, 2024, 33(4), 040202. [16] S. M. I. Hassan and A. A. Altwaty, Optical solitons of the extended Gerdjikov-Ivanov equation in DWDM system by extended simplest equation method, Appl. Math. Inf. Sci., 2020, 14(5), 901–907. [17] B. He and Q. Meng, Bifurcations and new exact travelling wave solutions for the Gerdjikov-Ivanov equation, Communications in Nonlinear Sci. Numerical Simulat., 2010, 15, 1783–1790. [18] K. K. Al-Kalbani, K. S. Al-Ghafri, E. V. Krishnan, et al., Solitons and modulation instability of the perturbed Gerdjikov-Ivanov equation with spatio-temporal dispersion, Chaos, Solitons and Fractals, 2021, 153, 111523. [19] D. J. Kaup and A. C. Newell, An exact solution for a derivative nonlinear Schrödinger equation, J. Math. Phys., 1978, 19(4), 798. [20] A. Ke and J. Li, Exact solutions and dynamics of Kundu-Mukherjee-Naskar model, Journal of Applied Analysis & Computation, 2024, 14(2), 1014–1022. [21] M. M. A. Khater, Abundant wave solutions of the perturbed Gerdjikov-Ivanov equation in telecommunication industry, Modern Phys. Lett. B, 2021, 35(26), 2150456. [22] M. M. A. Khater, X. Zhang and R. A. M. Attia, Accurate computational simulations of perturbed Chen-Lee-Liu equation, Results in Physics, 2023, 45, 106227. [23] N. A. Kudryashov, First integrals and solutions of the traveling wave reduction for the Triki-Biswas equation, Optik-International Journal for Light and Electron Optics, 2019, 185, 275–281. [24] N. A. Kudryashov and S. F. Lavrova, Painlevé analysis of the traveling wave reduction of the third-order derivative nonlinear Schrödinger equation, Mathematics, 2024, 12, 1632. [25] J. Li, Singular Nonlinear Traveling Wave Equations: Bifurcations and Exact Solutions, Science Press, Beijing, 2013. [26] M. Li, R. Ye and Y. Lou, Exact solutions of the nonlocal Gerdjikov-Ivanov equation, Communications in Theoretical Physics, 2021, 73(10), 105005. [27] Y. Li, L. Zhang, B. Hu and R. Wang, The initial-boundary value for the combined Schrödinger and Gerdjikov-Ivanov equation on the half-line via the Riemann-Hilbert approach, (Russian) Teoret. Mat. Fiz., 2021, 209(2), 258–273. [28] N. Liu, J. Y. Sun and J. D. Yu, Inverse scattering and soliton dynamics for the mixed Chen-Lee-Liu derivative nonlinear Schrödinger equation, Applied Mathematics Letters, 2024, 152, 109029. [29] Y. Lou, Y. Zhang, R. Ye and M. Li, Modulation instability, higher-order rogue waves and dynamics of the Gerdjikov-Ivanov equation, Wave Motion, 2021, 106, 102795. [30] P. Lu, Y. Wang and C. Dai, Abundant fractional soliton solutions of a space-time fractional perturbed Gerdjikov-Ivanov equation by a fractional mapping method, Chinese J. Phys., 2021, 74, 96–105. [31] J. Luo and E. Fan, ∂-dressing method for the coupled Gerdjikov-Ivanov equation, Appl. Math. Lett., 2020, 110, 106589. ∂-dressing method for the coupled Gerdjikov-Ivanov equation" target="_blank">Google Scholar
[32] J. Luo and E. Fan, Dbar-dressing method for the Gerdjikov-Ivanov equation with nonzero boundary conditions, Appl. Math. Lett., 2021, 120, 107297. [33] A. Saima, Sub-pico second chirped optical pulses with Triki-Biswas equation by e−Φ(ξ)-expansion method and the first integral method, Optik, 2019, 179, 518–525. [34] H. Triki and A. Biswas, Sub pico-second chirped envelope solitons and conservation laws in monomode optical fibers for a new derivative nonlinear Schrödinger's model, Optik-International Journal for Light and Electron Optics, 2018, 173, 235–241. [35] T. Tsuchida, Integrable discretizations of derivative nonlinear Schrödinger equations, Journal of Physics A General Physics, 2002, 35, 7827–7847. [36] Vinita and S. S. Ray, Lie symmetry reductions, power series solutions and conservation laws of the coupled Gerdjikov-Ivanov equation using optimal system of Lie subalgebra, Z. Angew. Math. Phys., 2021, 72(4), 133. [37] K. L. Wang, Novel solitary wave and periodic solutions for the nonlinear Kaup-Newell equation in optical fibers, Opt. Quant. Electron., 2024, 514, 56. [38] K. L. Wang, G. D. Wang and F. Shi, Sub-picosecond pulses in single-mode optical fibres with the Kaup-Newell model via two innovative methods, Pramana-J. Phys., 2024, 26, 98. [39] X. Xiao and Z. Yin, Exact single travelling wave solutions to the fractional perturbed Gerdjikov-Ivanov equation in nonlinear optics, Modern Phys. Lett. B, 2021, 35, 22. [40] Q. Xu and C. Zhang, Bifurcation analysis and chaos of a modified Holling-Tanner model with discrete time, Journal of Applied Analysis & Computation, 2024, 14(6), 3425–3449. [41] L. Xue and Q. Zhang, Soliton solutions of derivative nonlinear Schrödinger equations: Conservative schemes and numerical simulation, Physica D: Nonlinear Phenomena, 2024, 470, 134372. [42] S. S. Zhang, T. Xu, M. Li and X. F. Zhang, Higher-order algebraic soliton solutions of the Gerdjikov-Ivanov equation: Asymptotic analysis and emergence of rogue waves, Phys. D, 2022, 432, 133128. [43] Z. Zhang and E. Fan, Inverse scattering transform and multiple high-order pole solutions for the Gerdjikov-Ivanov equation under the zero/nonzero background, Z. Angew. Math. Phys., 2021, 72(4), 153. [44] Z. Zhang and E. Fan, Inverse scattering transform for the Gerdjikov-Ivanov equation with nonzero boundary conditions, Z. Angew. Math. Phys., 2020, 71(5), 149. [45] Y. Zhou and J. Zhuang, Bifurcations and exact solutions of the Raman soliton model in nanoscale optical waveguides with metamaterials, Journal of Nonlinear Modeling and Analysis, 2021, 3(1), 145–165. [46] J. Zhu and Y. Chen, A new form of general soliton solutions and multiple zeros solutions for a higher-order Kaup-Newell equation, J. Math. Phys., 2021, 62, 123501. [47] J. Zhuang, Y. Zhou and J. Li, Bifurcations and exact solutions of the derivative nonlinear Schrödinger equations DNLSI-DNLSIII: Dynamical system method, to appear. -
-
-
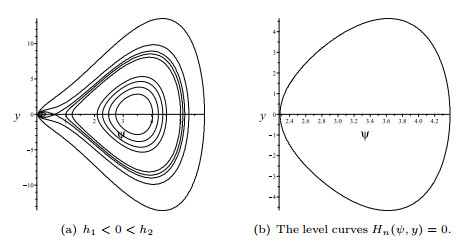
Figure 1.
Bifurcations of phase portraits of system (1.16) when
$ \alpha_1>0, \alpha_2\in R, \alpha_3<0. $ -
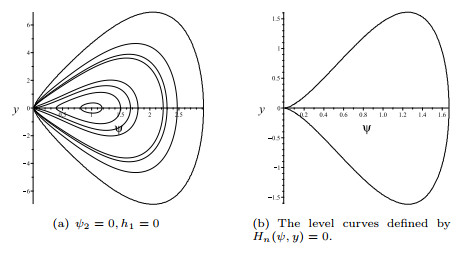
Figure 2.
Bifurcations of phase portraits of (1.16) when
$ \alpha_1<0,\alpha_2>0,\frac{(2n+1)\alpha_2^2}{4(n+1)^2\alpha_1}<\alpha_3<0. $ -
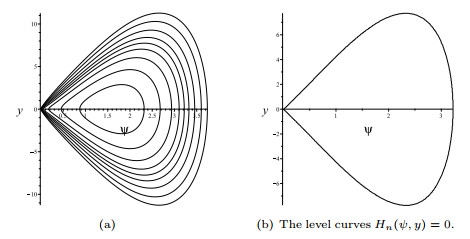
Figure 3.
Bifurcations of phase portraits of system (1.16) when
$ \alpha_1=0, \alpha_2>0, \alpha_3<0. $




 DownLoad:
DownLoad: