| Citation: | Qing Zhang, Zhengdong Du. ON THE LYAPUNOV CONSTANTS OF PLANAR PIECEWISE SMOOTH SYSTEMS SEPARATED BY AN ANALYTICAL CURVE[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 3128-3158. doi: 10.11948/20240503 |
ON THE LYAPUNOV CONSTANTS OF PLANAR PIECEWISE SMOOTH SYSTEMS SEPARATED BY AN ANALYTICAL CURVE
-
Abstract
In this paper, we consider the computations of Lyapunov constants of a class of planar piecewise analytical systems defined in two zones separated by an analytical curve $ y=\phi(x) $ with $ \phi(0)=0 $. Assume that the origin $ (0, 0) $ is a pseudo-focus of the system. We propose an extension of the classical polar coordinates for the subsystem with focus contact, and an extension of the $ (R, \theta, 1, 2) $-generalized polar coordinates for the subsystem with parabolic contact. Then we present the method on how to calculate the relevant Lyapunov constants. As applications, we present three planar piecewise quadratic systems. The first one is of parabolic-parabolic type separated by $ y=\sin^2 x $ which has four limit cycles bifurcated from $ (0, 0) $. The second one is of focus-parabolic type separated by $ y=e^x-1 $ which has five limit cycles bifurcated from $ (0, 0) $. The last one is of focus-focus type separated by $ y=\sin x $ which has five limit cycles bifurcated from $ (0, 0) $.
-

-
References
[1] K. da S. Andrade, O. A. R. Cespedes, D. R. Cruz and D. D. Novaes, Higher order Melnikov analysis for planar piecewise linear vector fields with nonlinear switching curve, J. Differ. Equ., 2021, 287, 1–36. doi: 10.1016/j.jde.2021.03.039 [2] J. L. R. Bastos, C. A. Buzzi and J. Torregrosa, Cyclicity near infinity in piecewise linear vector fields having a nonregular switching line, Qual. Theory Dyn. Syst., 2023, 22(4), 125, 11 pages. [3] D. de Carvalho Braga, A. F. da Fonseca, L. F. Gonçalves and L. F. Mello, Lyapunov coefficients for an invisible fold-fold singularity in planar piecewise Hamiltonian systems, J. Math. Anal. Appl., 2020, 484(1), 123692, 19 pages. [4] D. de Carvalho Braga and L. F. Mello, More than three limit cycles in discontinuous piecewise linear differential systems with two zones in the plane, Internat. J. Bifur. Chaos, 2014, 24(4), 1450056, 10 pages. [5] P. T. Cardin and J. Torregrosa, Limit cycles in planar piecewise linear differential systems with nonregular separation line, Phys. D, 2016, 337, 67–82. doi: 10.1016/j.physd.2016.07.008 [6] V. Carmona, F. Fernández-Sánchez and D. D. Novaes, Uniform upper bound for the number of limit cycles of planar piecewise linear differential systems with two zones separated by a straight line, Appl. Math. Lett., 2023, 137, 108501, 8 pages. [7] T. Chen, L. Huang and P. Yu, Center condition and bifurcation of limit cycles for quadratic switching systems with a nilpotent equilibrium point, J. Differ. Equ., 2021, 303, 326–368. doi: 10.1016/j.jde.2021.09.030 [8] T. Chen and J. Llibre, Nilpotent center in a continuous piecewise quadratic polynomial hamiltonian vector field, Internat. J. Bifur. Chaos, 2022, 32(8), 2250116, 23 pages. [9] X. Chen, V. G. Romanovski and W. Zhang, Degenerate Hopf bifurcations in a family of FF-type switching systems, J. Math. Anal. Appl., 2015, 432(2), 1058–1076. doi: 10.1016/j.jmaa.2015.07.036 [10] B. Coll, A. Gasull and R. Prohens, Differential equations defined by the sum of two quasi-homogeneous vector fields, Canad. J. Math., 1997, 49(2), 212–231. doi: 10.4153/CJM-1997-011-0 [11] B. Coll, A. Gasull and R. Prohens, Degenerate Hopf bifurcations in discontinuous planar systems, J. Math. Anal. Appl., 2001, 253(2), 671–690. doi: 10.1006/jmaa.2000.7188 [12] L. P. C. da Cruz, D. D. Novaes and J. Torregrosa, New lower bound for the Hilbert number in piecewise quadratic differential systems, J. Differ. Equ., 2019, 266(7), 4170–4203. doi: 10.1016/j.jde.2018.09.032 [13] M. Esteban, E. Freire, E. Ponce and F. Torres, On normal forms and return maps for pseudo-focus points, J. Math. Anal. Appl., 2022, 507(1), 125774, 31 pages. [14] E. Freire, E. Ponce, F. Rodrigo and F. Torres, Bifurcation sets of continuous piecewise linear systems with two zones, Internat. J. Bifur. Chaos, 1998, 8(11), 2073–2097. doi: 10.1142/S0218127498001728 [15] A. Gasull, Some open problems in low dimensional dynamical systems, SeMA J., 2021, 78(3), 233–269. doi: 10.1007/s40324-021-00244-3 [16] A. Gasull and J. Torregrosa, Center-focus problem for discontinuous planar differential equations, Internat. J. Bifur. Chaos, 2003, 13(7), 1755–1765. doi: 10.1142/S0218127403007618 [17] A. Gasull, J. Torregrosa and X. Zhang, Piecewise linear differential systems with an algebraic line of separation, Electron. J. Differential Equations, 2020, Paper No. 19, 14 pages. [18] L. F. S. Gouveia and J. Torregrosa, Local cyclicity in low degree planar piecewise polynomial vector fields, Nonlinear Anal.-Real World Appl., 2021, 60, 103278, 19 pages. [19] M. Han, Liapunov constants and Hopf cyclicity of Liénard systems, Ann. Differential Equations, 1999, 15(2), 113–126. [20] M. Han, Bifurcation Theory of Limit Cycles, Science Press, Beijing, 2013. [21] M. Han and S. Liu, Hopf bifurcation in a class of piecewise smooth near-Hamiltonian systems, Bull. Sci. Math., 2024, 195, 103471, 30 pages. [22] M. Han and J. Yang, The maximum number of zeros of functions with parameters and application to differential equations, J. Nonlinear Modeling and Analysis, 2021, 3(1), 13–34. [23] M. Han and W. Zhang, On Hopf bifurcation in non-smooth planar systems, J. Differ. Equ., 2010, 248(9), 2399–2416. doi: 10.1016/j.jde.2009.10.002 [24] H. A. Hosham, Bifurcation of periodic orbits in discontinuous systems, Nonlinear Dynam., 2017, 87, 135–148. doi: 10.1007/s11071-016-3031-7 [25] S. Huan and X. Yang, On the number of limit cycles in general planar piecewise linear systems, Discrete Contin. Dyn. Syst., 2012, 32(6), 2147–2164. doi: 10.3934/dcds.2012.32.2147 [26] S. Huan and X. Yang, Limit cycles in a family of planar piecewise linear differential systems with a nonregular separation line, Internat. J. Bifur. Chaos, 2019, 29(8), 1950109, 22 pages. [27] A. Ke, M. Han and W. Geng, The number of limit cycles from the perturbation of a quadratic isochronous system with two switching lines, Commun. Pure Appl. Anal, 2022, 21(5), 1793-1809. doi: 10.3934/cpaa.2022047 [28] Yu. A. Kuznetsov, S. Rinaldi and A. Gragnani, One-parameter bifurcations in planar Filippov systems, Internat. J. Bifur. Chaos, 2003, 13(8), 2157–2188. doi: 10.1142/S0218127403007874 [29] T. Li and J. Llibre, Limit cycles in piecewise polynomial Hamiltonian systems allowing nonlinear switching boundaries, J. Differ. Equ., 2023, 344, 405–438. doi: 10.1016/j.jde.2022.11.007 [30] F. Liang, V. G. Romanovski and D. Zhang, Limit cycles in small perturbations of a planar piecewise linear Hamiltonian system with a non-regular separation line, Chaos Solit. Fract., 2018, 111, 18–34. doi: 10.1016/j.chaos.2018.04.002 [31] H. Liu, Z. Wei and I. Moroz, Limit cycles and bifurcations in a class of planar piecewise linear systems with a nonregular separation line, J. Math. Anal. Appl., 2023, 526(2), 127318, 25 pages. [32] S. Liu and M. Han, Limit cycle bifurcations near double homoclinic and double heteroclinic loops in piecewise smooth systems, Chaos Solit. Fract., 2023, 175, 113970, 11 pages. [33] S. Liu and M. Han, Homoclinic and heteroclinic bifurcations in piecewise smooth systems via stability-changing method, Comput. Appl. Math., 2024, 43(5), 274, 24 pages. [34] X. Liu, X. Yang and S. Huan, Existence of four-crossing-points limit cycles in planar sector-wise linear systems with saddle-saddle dynamics, Qual. Theory Dyn. Syst., 2022, 21(3), 63, 31 pages. [35] J. Llibre and A. C. Mereu, Limit cycles for discontinuous quadratic differential systems with two zones, J. Math. Anal. Appl., 2014, 413(2), 763–775. doi: 10.1016/j.jmaa.2013.12.031 [36] J. Llibre and E. Ponce, Piecewise linear feedback systems with arbitrary number of limit cycles, Internat. J. Bifur. Chaos, 2003, 13(4), 895–904. doi: 10.1142/S0218127403007047 [37] J. Llibre, E. Ponce and X. Zhang, Existence of piecewise linear differential systems with exactly $n$ limit cycles for all $n \in \mathbb{N}$, Nonlinear Anal., 2003, 54(5), 977–994. doi: 10.1016/S0362-546X(03)00122-6 CrossRef $n$ limit cycles for all
$n \in \mathbb{N}$ [38] R. Lum and L. O. Chua, Global properties of continuous piecewise linear vector fields, part I: Simplest case in $\mathbb{R}^2$, Int. J. Circuit Theory Appl., 1991, 19(3), 251–307. doi: 10.1002/cta.4490190305 [39] D. D. Novaes, On the Hilbert number for piecewise linear vector fields with algebraic discontinuity set, Phys. D, 2022, 441, 133523, 15 pages. [40] D. D. Novaes and L. A. Silva, Lyapunov coefficients for monodromic tangential singularities in Filippov vector fields, J. Differ. Equ., 2021, 300, 565–596. doi: 10.1016/j.jde.2021.08.008 [41] C. Pessoa and R. Ribeiro, Bifurcation of limit cycles from a periodic annulus formed by a center and two saddles in piecewise linear differential system with three zones, Nonlinear Anal.-Real World Appl., 2024, 80, 104171, 17 pages. [42] L. Sun and Z. Du, Crossing limit cycles in planar piecewise linear systems separated by a nonregular line with node-node type critical points, Internat. J. Bifur. Chaos, 2024, 34(4), 2450049, 23 pages. [43] H. Tian and M. Han, Limit cycle bifurcations of piecewise smooth near-Hamiltonian systems with a switching curve, Discrete Contin. Dyn. Syst. Ser. B, 2021, 26(10), 5581–5599. [44] Y. Tian and P. Yu, Center conditions in a switching Bautin system, J. Differ. Equ., 2015, 259(3), 1203–1226. doi: 10.1016/j.jde.2015.02.044 [45] D. Weiss, T. Küpper and H. A. Hosham, Invariant manifolds for nonsmooth systems with sliding mode, Math. Comput. Simulation, 2015, 110, 15–32. doi: 10.1016/j.matcom.2014.02.004 [46] L. Xiong, K. Wu and S. Li, Global dynamics of a degenerate planar piecewise linear differential system with three zones, Bull. Sci. Math., 2023, 184, 103258, 27 pages. [47] Y. Xiong and M. Han, Limit cycle bifurcations in discontinuous planar systems with multiple lines, J. Appl. Anal. Comput., 2020, 10(1), 361–377. [48] Y. Zou and T. Küpper, Generalized Hopf bifurcation emanated from a corner for piecewise smooth planar systems, Nonlinear Anal., 2005, 62(1), 1–17. doi: 10.1016/j.na.2004.06.004 [49] Y. Zou, T. Küpper and W.-J. Beyn, Generalized Hopf bifurcation for planar Filippov systems continuous at the origin, J. Nonlinear Sci., 2006, 16(2), 159–177. doi: 10.1007/s00332-005-0606-8 -
-
-
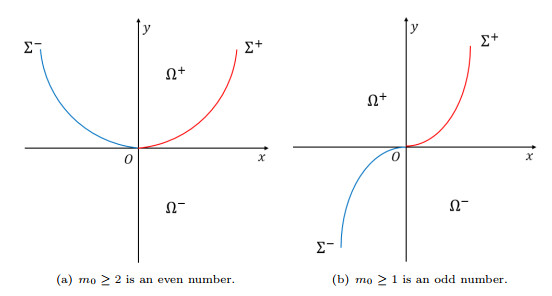
Figure 1.
The two zones
$ \Omega^{+} $ $ \Omega^{-} $ $ y=\phi(x)=x^{m_0}+O(x^{m_0+1}) $ -
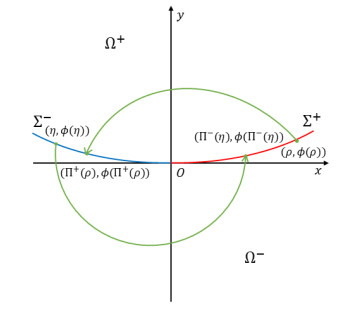
Figure 2.
The construction of the positive and the negative half-return maps.
-
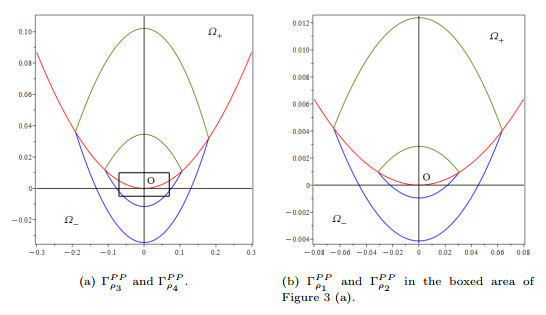
Figure 3.
The four limit cycles of system (2.11) corresponding to the parameters
$ \xi=\xi_0+\bar{\xi} $ -
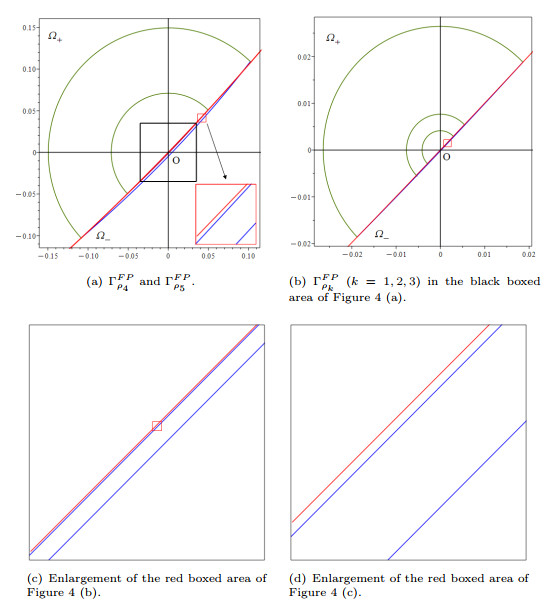
Figure 4.
The five limit cycles of system (2.12) corresponding to the parameters
$ \eta=\eta_0+\bar{\eta} $ -
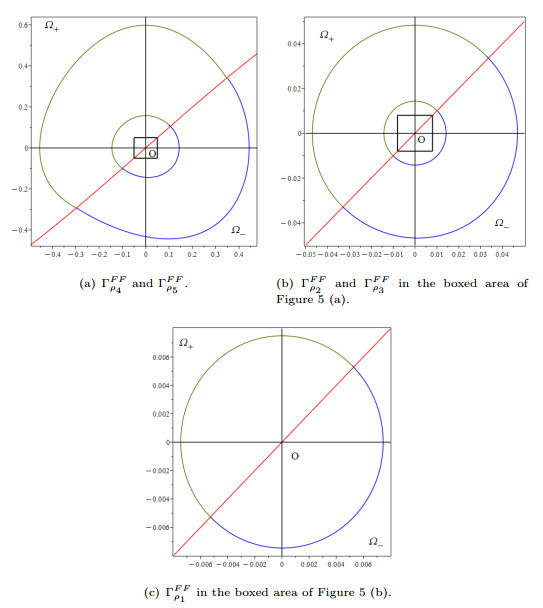
Figure 5.
The five limit cycles of system (2.12) corresponding to the parameters
$ \zeta=\zeta_0+\bar{\zeta} $




 DownLoad:
DownLoad: